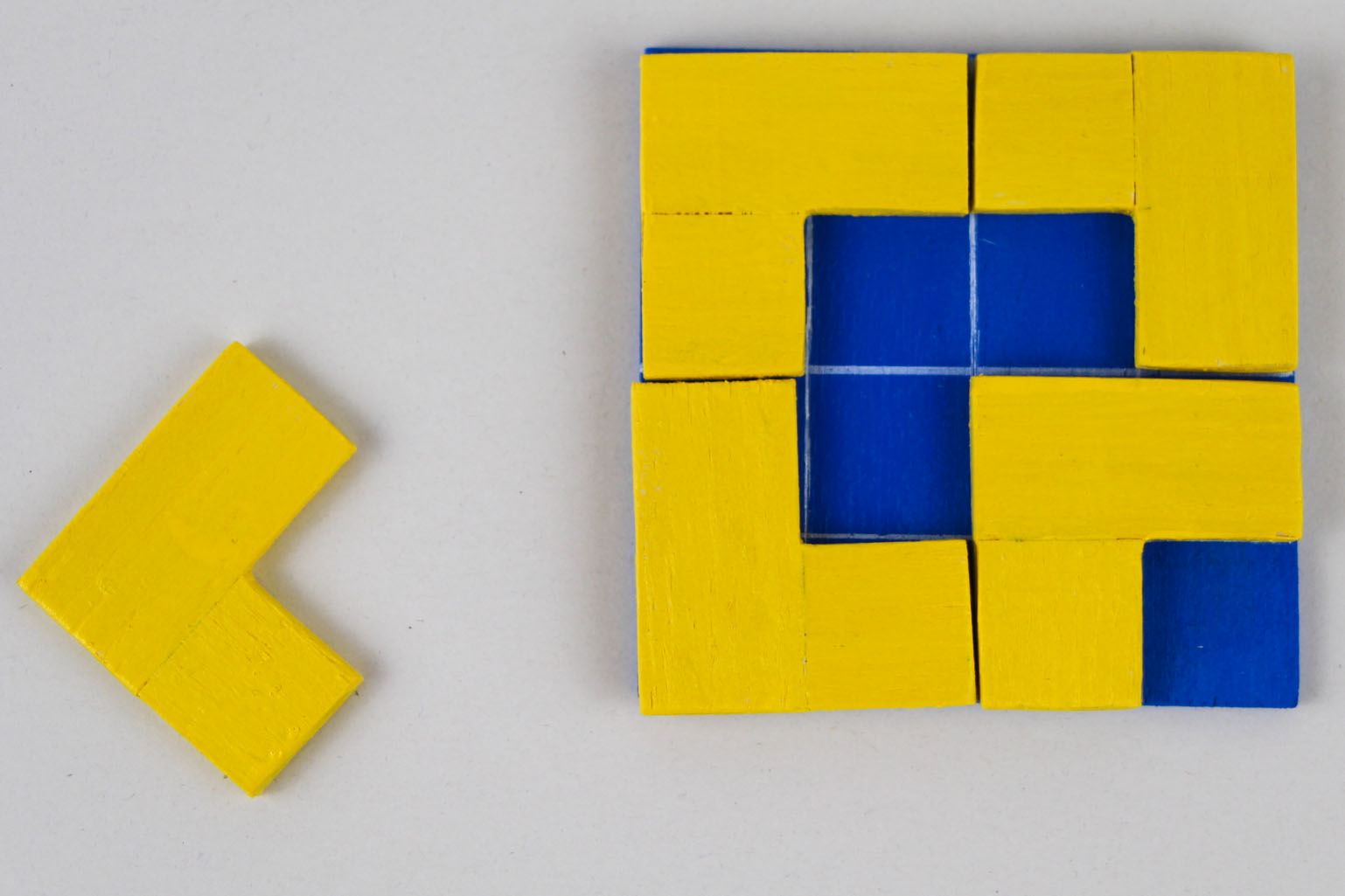Jedes Quadrat der Länge 2, 4, 8, 16, 32, … (oder mit der Länge 2n, wobei n den Wert jeder natürlichen Zahl annehmen kann) lässt sich mit “Winkeln”, die aus drei Quadraten zusammengesetzt sind (im Exponat gelb) so belegen, dass nur ein Eckquadrat frei bleibt.
Um diese Behauptung zu beweisen, könnte man natürlich versuchen, für jedes solche Quadrat eine Lösung zu finden. Wegen unserer menschlichen Endlichkeit würden wir aber nur eine – vielleicht sehr große – Anzahl von Fällen überprüfen können. Aber noch so viele geprüfte Beispiele lieferten uns nicht die absolute Sicherheit, dass nicht doch demnächst jemand ein Quadrat finden könnte, bei dem so eine Bedeckung nicht möglich ist.
Wir betrachten zunächst die Fälle n=2, n=4 und n=8.
Die Behauptung von oben wird bestätigt.
Wir erkennen eine Struktur, die uns vielleicht weiterhilft.
Diese ständig zu erweiternde Struktur führt uns zu folgender Erkenntnis.
Wir können uns nun von der Richtigkeit folgender Aussagen überzeugen:
Erstens: Für das 2×2-Quadrat gilt unsere Behauptung.
Zweitens: Wenn wir die Lösung für das 2nx2n-Quadrat voraussetzen dürfen, so können wir wie oben aus vier solchen Quadraten ein 2n+1x2n+1-Quadrat so belegen, dass in die Mitte ein zusätzlicher gelber Winkel passt und die rechte untere Ecke frei bleibt. Abstrahierend von unserem Beispiel können wir das für alle natürlichen Zahlen n=1, 2, 3, 4, 5, usw. bestätigen.
Damit können wir ganz sicher sein, dass unsere Ausgangsbehauptung für alle solche Quadrate wahr ist.
Dieses tolle Beweisverfahren in der Mathematik nennt man Beweis durch vollständige Induktion.
“Erstens” nennt man die Induktionsverankerung oder den Induktionsanfang.
“Zweitens” nennt man den Induktionsschritt.
Was meinst Du zu folgender Anwendung:
Erstens: in jeden Koffer passt ein Paar Socken.
Zweitens: Wenn n Paar Socken in den Koffer passen, dann kriegt man auch noch ein Paar in den Koffer, also n+1 Paare. Diese Aussage muss für alle natürlichen Zahlen gelten.
Ergo passen unendlich viele Sockenpaare in den Koffer.