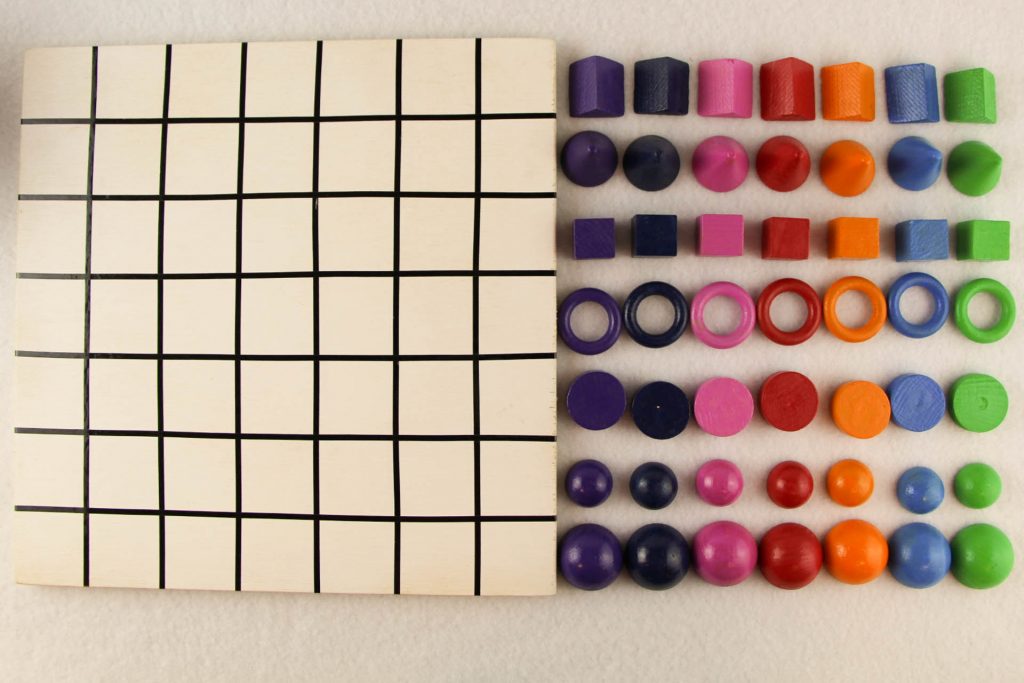Ein lateinisches Quadrat ist ein quadratisches Schema, das aus n Zeilen und n Spalten besteht. Auf die so entstehenden n2 Felder werden n Symbole (grüner, roter, blauer, gelber und oranger Kreis oder Zylinder) so verteilt, dass in jeder Zeile und jeder Spalte jedes Symbol vorkommt, was auch bedeutet, dass jedes der n Symbole höchstens einmal vorkommt, also jedes Symbol kommt in jeder Zeile und jeder Spalte genau einmal vor. Hier ist ein Beispiel:
Bei diesem Beispiel eines lateinischen Quadrats gilt n=5 und die gelben, roten, orangen, blauen und grünen zylinderförmigen Steine sind die n=5 unterscheidbaren Symbole. Da in keiner der Zeilen und in keiner Spalte eines der fünf Symbole mehrfach vorkommt, aber auch mindestens einmal vorkommt, handelt es sich hier tatsächlich um ein lateinisches Quadrat. Es gibt sehr viele Lösungen für die Aufgabe, aus den 25 Elementen mit den fünf Farben ein 5×5-Schema zu einem lateinischen Quadrat zu machen. Hier im Beispiel ist noch eine Zusatzbedingung erfüllt worden, dass auch in den Diagonalen kein Symbol mehrmals vorkommt. Diese Möglichkeit, lateinische Quadrate herzustellen, die noch weitere Eigenschaften haben oder Bedingungen erfüllen, ist ein Hauptgrund für die breite Anwendung des lateinischen Quadrates. Es war einer der fruchtbarsten Mathematiker, nämlich Leonhard Euler (1707-1783), der sich u.a. mit solchen Quadraten beschäftigte. Da Euler als Symbole lateinische Buchstaben benutzte, entstand die Bezeichnung lateinische Quadrate.
Wenn ein lateinisches Quadrat so aufgebaut ist, dass die Symbole in den Zeilen und Spalten bei Beibehaltung einer bestimmten Reihenfolge “wandern”, spricht man von einem zyklischen lateinischen Quadrat. Dabei entsteht die zweite Zeile dadurch, dass alle Symbole der ersten Zeile einen Platz nach links rücken und das erste Element der vorhergehenden Zeile auf den letzten Platz der zweiten Zeile rückt. Dieser Tausch wird mit jeder weiteren Zeile wiederholt. Man kann diese Verschiebungen der Symbole mit jedem entstandenen zyklischen Quadrat erneut machen und erhält wieder ein zyklisches Quadrat. Bei unserem Beispiel mit den farbigen Kreisen tritt nach fünf solcher zyklischen Vertauschungen wieder das Ausgangsquadrat auf, bei n Symbolen nach n zyklischen Vertauschungen.
Ein wichtiges Beispiel für ein zyklisches lateinisches Quadrat ist die oben abgebildete Vigenère-Tabelle. Sie ist eine Weiterentwicklung aus der Caesar-Scheibe und dient zur Verschlüsselung von Texten. Die 26 Buchstaben unseres Alphabets sind die 26 Symbole eines lateinischen Quadrats der Ordnung n=26. In jeder Zeile und in jeder Spalte befinden sich alle 26 Buchstaben, also auch keiner mehr als einmal. Das geschieht dadurch, dass nur in der ersten Zeile und in der ersten Spalte die Buchstabenfolgen mit A beginnen, die zweite Zeile und Spalte beginnen mit B, die dritte mit C usw. Die Reihenfolge der Buchstaben entspricht in allen Zeilen und Spalten der gewöhnlichen Anordnung des Alphabets. Die beiden Eingänge der Vigenère-Tabelle dienen dazu, jeden Buchstaben des Klartextes mit einem besonderen Schlüssel umzuwandeln.
Das Vokal-Quadrat ist eine kleine Herausforderung: Gelöst ist es, wenn die freien Plätze so mit den fünf Vokalen aus dem Kästchen belegt sind, dass ein lateinisches Quadrat vorliegt.
Zwei lateinische Quadrate der Ordnung n (n Symbole) können, wenn man sie übereinander legt, wieder ein lateinisches Quadrat ergeben. In den n Zeilen und n Spalten des neuen Quadrates befinden sich dann jeweils n2 verschiedene Symbolpaare. Falls dabei keine zwei gleiche Symbolpaare in einer Zeile oder einer Spalte platziert sind, ist das zusammengesetzte Quadrat auch ein lateinisches Quadrat. In der Mathematik nennt man zwei lateinische Quadrate der Ordnung n mit dieser Eigenschaft orthogonal. Zum besseren Verständnis gibt es in der Mathothek die Möglichkeit mit einem 4×4-Brett und schwarzen und weißen Chips, die jeweils die Zahlen 1, 2, 3 und 4 tragen, zwei lateinische Quadrate so zu legen, dass die beiden zusammen ein griechisch-lateinisches Quadrat ergeben.
Wie man leicht nachprüfen kann, bilden die vier Symbole 1, 2, 3 und 4 auf den weißen Chips für sich genommen ein lateinisches Quadrat und ebenso die Symbole 1,2,3 und 4 auf den schwarzen Chips. Übereinandergelegt ergeben diese beiden lateinischen Quadrate mit den 16 Symbolpaaren (1/1), (2/2), (3/3), (4/4), (2/4), (1/3), (4/2), (3/1), (3/2), (4/1), (1/4), (2/3), (4/3), (3/4), (2/1) und (1/2) wieder ein lateinisches Quadrat ( in keiner Zeile und auch in keiner Spalte gibt es ein Zahlenpaar mehr als einmal). Die beiden lateinischen Ausgangsquadrate sind also orthogonal und die Kombination dieser beiden orthogonalen lateinischen Quadrate nennt man ein griechisch-lateinisches Quadrat. Der Name kommt ebenfalls von Euler, weil er für die Ausgangsquadrate lateinische bzw. griechische Buchstaben benutzte.
Wir betrachten nun ein weiteres Exponat der Mathothek, bei dem es um vier Formen und vier Farben geht. Bei dem Beispiel (rechts) sehen wir ein griechisch-lateinisches Formen-Farben-Quadrat: Jede der vier Farben und vier Formen kommen in jeder Zeile und jeder Spalte genau einmal vor.
Bei dem nächsten Beispiel eines griechisch-lateinischen Farben-Formen-Quadrates sehen wir wieder, dass die jeweils vier Farb-Symbole und vier Form-Symbole zu 4⋅4=16 unterscheidbaren Symbolen kombiniert worden sind. Das neue Farben-Formen-Quadrat erfüllt, wovon man sich leicht überzeugen kann, die Bedingung, dass in keiner Zeile oder Spalte eines der Symbole mehrfach vorkommt. Es ist also ein weiteres Beispiel für ein griechisch-lateinisches Quadrat. Wenn man den Zahlen 1, 2, 3 und 4 auf den weißen Chips die Farben grün, blau, gelb und rot und den Zahlen 1, 2, 3 und 4 auf den schwarzen Chips die Formen Kreis, Dreieck, Oval und Quadrat zuordnet, dann wird die gemeinsame Struktur der beiden Quadrate sichtbar und es lassen sich die beschriebenen Zusammenhänge gut erkennen.
Zur Erholung folgt hier eine Abbildung des kleinsten griechisch-lateinischen Quadrates mit drei Formen und drei Farben. Das Brett und die neun Figuren gehören zu “dem ultimativen Logikspiel, das einen nicht mehr loslässt”, das auch in der Mathothek präsent ist.
Während es in dem Fall n=4 noch relativ einfach ist, eine Lösung zu finden, ist das für das nächste griechisch-lateinische Quadrat der Ordnung n=7 schon beachtlich schwieriger.
Besonders schön ist die Lösung, bei der die beiden Diagonalen benutzt werden. Trotzdem ist jede Lösung eine große Herausforderung an Phantasie, Logik und Geduld des Besuchers.
Dieses 7×7-Brett mit seinen 49 Symbolen, das sind alle Kombinationen aus 7 Farben und 7 geometrischen Körpern, hat mehrere Lösungen. Die hier abgebildete Lösung benutzt konstruktiv die beiden Hauptdiagonalen. Dieses Objekt lässt sich auch dazu benutzen, sich an griechisch-lateinischen Quadraten der Ordnungen n=2, 3, 4, 5 und 6 zu versuchen: Man teilt ein entsprechend großes nxn-Quadrat ab und wählt n Formen und n Farben aus. Bei n=2 ist leicht einzusehen, dass es kein griechisch-lateinisches Quadrat der Ordnung 2 gibt. Dass im Falle n=6 ebenfalls jeder Lösungsaufwand vergebene Liebesmüh ist, war es doch selbst für den großen Mathematiker Leonhard Euler nur eine Vermutung, die er nicht beweisen konnte und die erst viel, viel später bewiesen wurde.
Bei dem nächsten Beispiel eines griechisch-lateinischen Quadrates wäre es für die allermeisten Besucher wohl eine zu große Zumutung – ohne jede Hilfe – eine Lösung zu finden. Es handelt sich hier um ein griechisch-lateinisches Quadrat der Ordnung n=10, bei dem es noch eine Menge Lücken richtig zu füllen gilt. Insgesamt sind 100 verschiedene Symbole, nämlich alle möglichen Kombinationen aus 10 Farben und 10 Formen, zu verteilen.
In diesem Fall gibt es nur eine richtige Ergänzung der noch freien Plätzen mit den restlichen Symbolen.
Bei dem oben abgebildeten Objekt aus der Mathothek geht es wieder um die Konstruktion eines lateinischen Quadrates, bei dem bereits einige Positionen vorgegeben sind. Zusätzlich sind dabei die eingetragenen Ungleichheitszeichen zu erfüllen. Auch hier handelt es sich um keine ganz leichte Herausforderung, aber die sie ist machbar:
Ein weiteres Exponat in der Mathothek hat ebenfalls mit einem lateinischen Quadrat gemeinsam, dass in keiner Zeile oder Spalte mehrfach dasselbe Symbol auftreten darf, aber nicht jedes auch vorkommen muss. Das geht, weil es sich um ein 4×4-Quadrat handelt, aber fünf Symbole zu verteilen sind.
Die Struktur des lateinischen Quadrats ist für viele andere besonderen Quadrate mit Zahlen, Buchstaben oder sonstigen Symbole der Ausgangspunkt. An den Beispielen sehen wir, dass die Struktur des lateinischen Quadrates sehr verbreitet ist. Die vielen Freiheiten, die das lateinische Quadrat noch lässt, erlauben es, weitere zu erfüllende Bedingungen an ein solches Quadrat zu stellen. Durch zusätzliche Bedingungen entstehen immer wieder neue interessante Aufgaben und Quadrate. Aber nicht alle Neuschöpfungen sind überzeugend. So auch ein Objekt, mit dem man ein griechisch-lateinisches Quadrat der Ordnung n=6 herstellen soll.
Schon der große Mathematiker Leonhard Euler, den man am Hofe der russischen Zarin Katharina der Großen gefragt hatte, ob es möglich sei, Vertreter von sechs Regimentern und sechs Dienstgraden in einem Quadrat so aufzustellen, dass in jeder waagrechten und jeder senkrechten Reihe kein Dienstgrad, aber auch kein Regiment mehr als einmal vorkomme, fand keine Lösung und vermutete, dass die Aufgabe unlösbar sei, konnte es aber nicht beweisen. Erst in jüngster Zeit wurde bewiesen, dass außer für n=2 und n=6 immer ein griechisch-lateinisches Quadrat existiert.
In der Mathothek steht allerdings anscheinend den Besuchern ein griechisch-lateinisches-Quadrat der Ordnung n=6 zur Verfügung. Die beiden Merkmale sind ein Mal sechs verschiedene graue Höhen und das andere Mal die sechs verschiedenen Farben:
Nur durch einen nicht so leicht zu findenden Trick im Inneren der Türme erscheint die Aufgabe doch lösbar. Ich finde diese Pseudolösung sehr unfair und nicht wünschenswert. Die tricklose Mathematik, die in dem Scheitern beim Suchen nach einer Lösung, und der Geschichte dieses Problems sind mehr als interessant und aufschlussreich genug.
Trotzdem kommt hier die “Pseudo”-Lösung”:
Zwei interessante und verbreitete Varianten des lateinischen Quadrates sind die magischen Quadrate, die sehr alt sind, und die Sudokus, die in neuerer Zeit ihren Siegeszug in der Welt der Rätsel- und Knobelfreunde erlebten.
Magische Quadrate sind lateinische Zahlenquadrate mit der weiteren Bedingung, dass die Summen der Zahlen in jeder Zeile und jeder Spalte sowie in den beiden Hauptdiagonalen immer gleichgroß sind.
Sudokus sind lateinische Quadrate mit neun Zeilen und neun Spalten, bei denen meistens die Zahlen 1 bis 9 als Symbole verwendet werden. Als zusätzliche Bedingung müssen auch in jedem der neun disjunkten Teilquadraten alle neun Symbole vorkommen.
Lateinische Quadrate spielen auch bei den Verknüpfungstafeln algebraischer Gruppen eine große Rolle, wie man an dem Exponat zur Symmetriegruppe des gleichseitigen Dreiecks sehen kann.
Die Exponate zu den Varianten des lateinischen Quadrats, die den Besuchern der Mathothek zur Verfügung stehen, sind in weiteren Artikeln des Katalogs beschrieben.