In der Mathothek gibt es sehr viele Exponate, wovon die meisten interaktiv zu nutzen sind, mit denen man verstehend erfahren kann, wie die Menschen im Laufe der Geschichte Zahlen und das Rechnen mit ihnen bis zum heutigen Rechner entwickelt haben. So kann man beispielsweise Nachbildungen von Objekten zur Multiplikation des genialen schottischen Mathematikers Napier: Der Napier’sche Schachbrett-Rechner und die Napier’schen Rechenstäbchen.
Natürlich haben im Zeitalter des Computers diese alten Algorithmen für das praktische Rechnen so gut wie keinen Nutzen mehr. Trotzdem lässt sich aus der Beschäftigung mit ihnen, ihrer historischen Entwicklung und den geistigen Leistungen, die dahinterstehen, viel Grundsätzliches erkennen und verstehen. Aus diesem Grund entstand auch das folgende nachempfundene interaktive Objekt. Dieses Verfahren zum Multiplizieren durch Rückführung der Multiplikation auf die einfacheren Vorgänge des Halbierens und Verdoppelns sowie des Addieren wird ägyptisches oder äthiopisches Multiplizieren, aber auch russische Bauernmultiplikation genannt, ist schon sehr alt und wird auch heute noch mancherorts verwendet.
Außer den kleinen Kieselsteinchen ist an diesem Objekt nichts alt. Macht nichts. Die drei Reihen von zusammenhängenden Halbkugeln könnten gut für entsprechende Kuhlen im Wüstensand oder aus getrocknetem oder gebranntem Ton bzw. Lehm gemacht sein. Allerdings waren es in Wirklichkeit wohl nur zwei Reihen solcher Kuhlen. Macht auch nichts. Unsere Kuhlen stammen vom Flohmarkt und bestehen – keine Ahnung weshalb – aus drei Reihen von halbkugelförmigen Vertiefungen aus Plastikmaterial. Auf jeden Fall sind sie hervorragend geeignet, mit ihnen das ägyptische oder äthiopische Multiplizieren nachzuvollziehen.
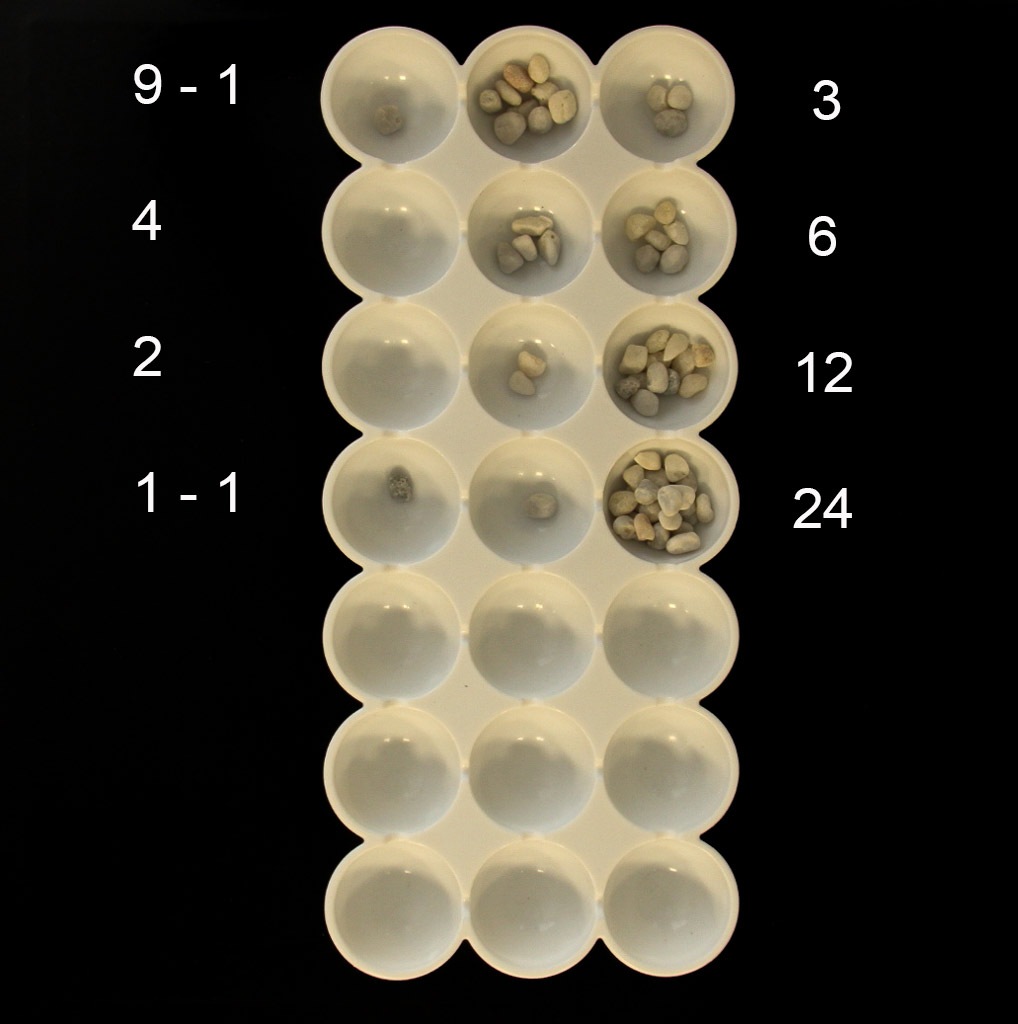
An dem Beispiel des Produkts 9⋅3 soll der Algorithmus gezeigt werden.
In die beiden Kuhlen in der Mitte und rechts der obersten Reihe legen wir neun bzw. drei Steinchen. Als ersten Schritt legen wir in die mittlere Kuhle der zweiten Reihe die halbe Anzahl von Steinchen der darüber befindlichen Kuhle. Da 9 sich nur mit dem Rest 1 halbieren lässt, legen wir diesen Rest in die oberste Kuhle links. In der mittleren Kuhle der zweiten Reihe liegen nun vier Steinchen. Die Hälfte davon beträgt zwei (ohne Rest). Also legen wir zwei Steinchen in die mittlere Kuhle der dritten Reihe. Die Hälfte von zwei ist eins (ohne Rest). Wir legen ein Steinchen in die mittlere Kuhle der vierten Reihe. 1 lässt sich nun zu 0 mit Rest 1 halbieren. Damit legen wir den Rest – ein Steinchen – in die linke Kuhle der vierten Reihe. In die mittlere Kuhle der fünften Reihe kommen null Steinchen.
Die beiden ersten senkrechten Reihen von Kuhlen sind fertig. Jetzt wird verdoppelt in der dritten Reihe: Aus drei Steinchen werden sechs in der darunter liegenden Kuhle. Zwölf Steinchen werden es in der darunter liegenden und 24 in der nächsten. Das gesuchte Produkt 9⋅3 erhalten wir zum Schluss, indem wir die Steinchen der Verdopplungsreihe addieren, aber nur die, bei denen in der linken Reihe ein “Rest-“Steinchen liegt. Die Summe von 3 und 24 ergibt 27. “Stimmt!”, sagt spätestens der Taschenrechner.
Man erkennt leicht, dass dieses klassische Verfahren auch ohne die dritte senkrechte Spalte funktioniert, wenn man anderweitig sich die waagrechten Reihen merkt, in der bei der Halbierung der Rest 1 auftritt, um so in der rechten Spalte die richtigen Zahlen zu addieren. Aber für eine Entfernung dieser dritten Kuhlen-Spalte besteht keine Notwendigkeit, sie erleichtert sogar das Verfahren. Mit freundlicher Empfehlung an die Altvorderen!
Es folgen – ohne Worte – noch drei weitere Beispiele: 8⋅5, 7⋅6 und 5⋅7:
Inzwischen gibt es in der Mathothek eine weitere Möglichkeit, auf die ägyptische oder äthiopische Art mit Kuhlen und Steinchen zu multiplizieren, die der ursprünglichen Form näher kommt. Das Vorgehen ist dabei prinzipiell das gleiche, wie bei drei Reihen von Kuhlen. Kurz gesagt, man verzichtet auf die mittlere Reihe.
Entscheidend ist es, dass am Ende die jeweiligen Kuhlenpaare mit Rest 1 links und dem zugehörigen Vielfachen rechts sichtbar sind.
Hier 6⋅2=12 als Beispiel:
Wir beginnen mit
Wir halbieren die sechs Steine links. Es bleibt kein Rest. Rechts verdoppeln wir die 2 zu 4 Steinen:
Im nächsten Schritt halbieren wir die 3 gibt 1 und den Rest 1. Rechts ergibt die Verdoppelung von 4 die 8 Steine.
Wir addieren jetzt die Steine rechts, bei denen links der Rest 1 war, 4 und 8 zu 12 und haben das Ergebnis der Multiplikation 6⋅2.
Statt der Plastikkuhlen oder auch zu Hause kann man die ägyptische Multiplikation auch sehr gut mit den Steinen und Kuhlen des Mancala-Spiels durchführen. Dieses beliebte afrikanische Strategiespiel ist auch in der Mathothek vorhanden.
Wer sich mit dem Binärsystem ein wenig auskennt, kann im Hintergrund der ägyptischen Multiplikation einen engen Zusammenhang erkennen. Diese Realisierung der äthiopischen Multiplikation mit den Kuhlen und Steinchen zeigt, dass für dieses Multiplikationsverfahren keine Kenntnis eines Zahlsystems oder von Zahlwörtern notwendig ist. Nur das Halbieren und Verdoppeln von Mengen aus Steinchen wird gebraucht sowie die Addition als Vereinigung entsprechender Mengen. Diese Behauptungen können auch gut anhand der Beispiele zur russischen Bauernmultiplikation erlebt werden.
Eine leichter zu benutzende Form der ägyptischen Multiplikation ist die sogenannte russische Bauernmultiplikation. Wieso dieses Multiplikationsverfahren diese Bezeichnung trägt, ist nicht klar. Statt mit Kuhlen und Steinchen funktioniert sie mit einer einfachen Tabelle mit zwei senkrechten Spalten und einer jeweils notwendigen Anzahl von waagrechten Zeilen. Im ersten Beispiel benutzen wir statt Steinchen oder Zahlen Strichziffern. Gesucht wird /////⋅/////:
///// /////
// ///// /////
/ ///// ///// ///// /////
Das Ergebnis beträgt also ///// ///// ///// ///// /////.
Beim nächsten Beispiel 17⋅19 benutzen wir indo-arabische Ziffern:
21 19
10 38
5 76
2 152
1 304
Das ergibt 21⋅19=304+76+19=399.
Natürlich funktioniert dieses Multiplikationsverfahren auch, wenn die “Russischen Bauern” mit römischen Ziffern rechnen:
XIV LIII
VII CVI
III CCXII
I CDXXIV
Dieses Mal stimmt die Rechnung auch: CVI+CCXII+CDXXIV=DCCXLII. Asterix meint allerdings wiedermal, dass die Römer spinnen. Und er übersetzt die Rechnung in das Dezimalsystem: 14⋅53=742. Natürlich sah Asterix, dass die russische Bauernmultiplikation ein intelligenter Algorithmus und mit praktisch jedem Zahlensystem möglich, aber die Rechnung mit den römischen Ziffern schrecklich unpraktisch ist.
Um zu zeigen, dass dieser Algorithmus der ägyptischen Multiplikation auch in das digitale Zeitalter passt, führen wir unser letztes Beispiel mit Binärzahlen durch: 25⋅12, in binärer Schreibweise ist das 11001⋅1100.
11001 1100
1100 11000
110 110000
11 1100000
1 11000000
Das Ergebnis ist 1100+1100000+11000000=100101100(=25610+3210+810+410=30010).
Im Binärsystem wird der Algorithmus der “russischen Bauernmultiplikation” völlig einfach: Letzte Ziffer 1⇔Zahl ist ungerade⇔Rest 1, Zahl halbieren ⇔ durch 10(=210) teilen ⇔ also eine 0 am Ende weglassen. Zahl verdoppeln ⇔ Zahl mit 10(=210) multiplizieren ⇔ eine 0 anhängen. Zum Schluss alle Zahlen der rechten Spalt streichen, wenn die Zahl in der linken Spalte gerade ist, d.h. letzte Ziffer eine 0 ist. Die Addition aller anderen Zahlen der rechten Spalte liefert das Ergebnis.
Versuche auch einmal, die chinesischen oder die Zahlzeichen der Maya zu verwenden. In der Mathothek gibt es viele spannende Exponate zu anderen Zahlendarstellungen und Systemen als dem aus guten Gründen weltweit verbreiteten Dezimalsystem.