Für “Zocker” müssen die beiden Spieler die Münzen, die sie einsetzen wollen und dann gewonnen oder verloren werden können, natürlich jeweils selbst zur Verfügung stellen. In der Mathothek handelt es sich nur um Leihgeld. Wie immer in der Mathothek geht es auch hier um das Gewinnen, aber nicht um den Gewinn von schnödem Mammon, sondern um den Gewinn von logischer und mathematischer Erfahrung und das für beide Spieler.

In der “freien Wildbahn” sieht das folgende Spiel so aus: Zwei Spieler legen 50 Münzen hintereinander in eine lange Reihe. Anschließend nehmen sie abwechselnd je eine Münze weg, und zwar ist das jeweils nur von einem der beiden Enden der Reihe erlaubt. Am Schluss wird der jeweilige Betrag, der Münzen, die jeder der beiden Spieler an sich genommen hat, ermittelt. Derjenige von beiden Spielern, der den größeren Betrag ergattert hat, bekommt auch noch die Münzen seines Gegenspielers.
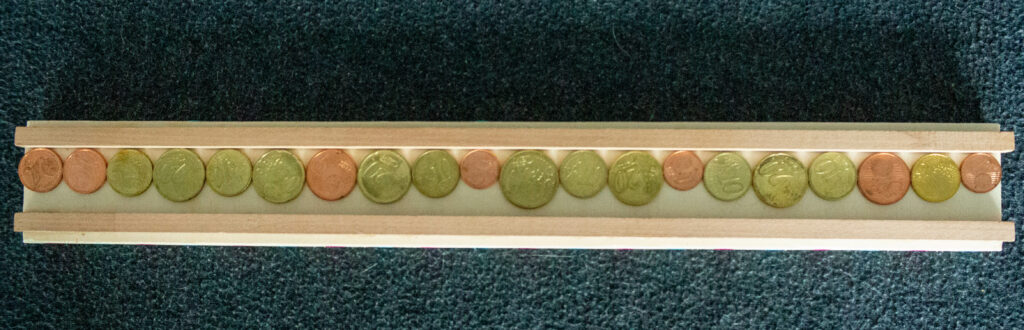
In der Mathothek werden zu Beginn alle vorhandenen Münzen hintereinander zwischen die beiden Leistchen gelegt. Die Reihenfolge darf großzügigerweise der Spieler A (=Ahnungsloser) bestimmen. Dafür darf der zweite Spieler B (=Bescheidwisser) als erster eine Münze von einem der beiden Enden der Münzreihe nehmen. Dann entscheidet sich A für seine Münze, die er entweder vom einen oder vom anderen Ende nehmen darf. Sind alle Münzen weggenommen, so wird jeweils für A und für B der Betrag der eingesammelten Münzen ermittelt, “and the winner takes it all”.
Natürlich wird vermutlich keiner der beiden Spieler, wenn er an der Reihe ist, die an einem der beiden Enden liegende kleiner Münze nehmen. Allerdings kann man sich auch leicht klarmachen, dass diese naheliegende Strategie noch lange keine sichere Gewinngarantie ist. Also stellt sich die Frage: Gibt es hier überhaupt eine sichere Gewinnstrategie?
Ja, es gibt sie, und zwar können wir uns in der Mathothek mit dem obigen Objekt davon überzeugen.

Zunächst ermittelt der eingeweihte Spieler B völlig unauffällig, ob die Münzen, die zu einem blauen Punkt gehören, oder die Münzen mit rotem Punkt den größeren Euro-Betrag liefern. Er entscheidet sich für die Farbe, die die größere Summe ergab. Im Beispiel hier beträgt der Wert aller Münzen zusammen 2,37 Euro. Kennt man den Wert aller Münzen bereits vor Spielbeginn, dann genügt es natürlich, eine der beiden Teilsummen zu zählen. Ist in unserem Beispiel, die ermittelte Summe größer als 2,37:2=1,185, also 1,19 oder größerer, dann wird A auf diese setzen und ihre Münzen Stück für Stück an sich nehmen und letztendlich alles gewinnen. Falls er 1,18 oder weniger gezählt hat, wird er sich für die andere Farbe und die entsprechende Reihe entscheiden. Anschließend nimmt er als Anfänger diejenige am Ende der Reihe liegende Münze mit der entsprechenden Farbe. Nun nimmt A seine Münze und egal, an welchem Ende der Reihe er seine Münze wegnimmt, für B bleibt eine Münze seiner Farbe an einem der beiden Enden übrig. Mit dieser Methode kann B seine gewinnbringenden Münzen einsammeln und somit den Gesamtbetrag einstreichen.
Will man verhindern, dass der Gegner die Strategie erkennt, dann ist es natürlich besser auf die farbigen Punkte zu verzichten und die Münzen gedanklich durchzunummerieren. Man ermittelt dann, ob die Münzen mit den geraden Zahlen oder die mit den ungeraden Zahlen den größeren Betrag liefern. Das bedeutet natürlich für B eine hohe Konzentration.
Auch in einem zweiten “Zockerspiel” geht es um jede Menge Euro. Und um eine runde Tortenplatte. Ede und Meister Eder haben je einen Säckchen voller Ein-Euro-Münzen gesammelt. Ede, der scharf auf Meister Eders Münzen ist, schlägt ihm deswegen folgendes Spiel vor: Sie legen ihre jeweiligen Münzen abwechselnd auf eine runde Tortenplatte, und zwar, sodass jede Ein-Euro-Münze flach und direkt auf der Platte liegt. Die einmal gelegten Münzen dürfen nicht mehr bewegt werden. Wer von beiden die letzte Münze legen kann, hat gewonnen und darf das gesamte Geld einstecken. Meister Eder, der ein großer Freund und Kenner von Symmetrien ist, stimmt sofort zu, allerdings mit der Bedingung, dass er anfangen darf. Ede hält das für fair, weil er irgendwie überzeugt ist, dass er dafür die letzte legen wird.
Meister Eder hat eine erfolgversprechende Idee. Er legt seine erste Münze genau auf den Mittelpunkt der kreisrunden Platte. Ede legt seine erste Münze an irgendeine Stelle – es ist ja noch viel Platz. Dann legt Meister Eder seine zweite Münze usw. Schließlich gibt es nur noch einen freien Platz, und zwar für Meister Eder, der grinsend daraufhin alle Euro einpackt und Ede mit verdutztem Gesicht stehenlässt.
Warum war Eder sich seiner Sache so sicher? Weil er als Schreiner auch ein Meister der Symmetrien ist, ganz besonders liebt er die Punktsymmetrie. Mit ihrer Hilfe hatte er blitzschnell seine sichere Strategie erkannt: Nachdem er den Mittelpunkt besetzt hatte, konterte er jeden Zug Edes, indem er seine Münze genau punktsymmetrisch zu dessen letzter Münze platzierte. So war er sich sicher, dass er immer einen punktsymmetrisch gelegenen Platz für seine Münze finden konnte, auch die letzte freie Stelle für seine Münze.
Auch “ohne finanzielle Mittel” kann diese Strategie in der Mathothek kennengelernt und geübt werden:


Meister Eders Kreisscheiben sind grün und Edes gelb.
Nebenbei bemerkt: Es handelt sich hier um die dichteste Kreispackung, die mathematisch möglich ist.
Das folgende Spiel für zwei Personen “20 gewinnt” ist ebenfalls ein Spiel mit Gewinngarantie für den beginnenden Spieler. Bei diesem Spiel werden zunächst 20 Spielsteine derselben Farbe auf den Tisch gelegt.
Die Spieler nehmen dann abwechselnd ein oder zwei Spielsteine weg. Derjenige Spieler, der den letzten Spielstein nehmen kann, gewinnt.

Hier aus einem Spielablauf:
Spieler I nimmt zwei Steine (es bleiben 18):

Spieler II nimmt einen Stein (es bleiben 17):

Nach weiteren Zügen besteht folgende Situation und Spieler I ist am Zug:

Spieler I nimmt einen Stein und sichert sich so den Sieg:

Spieler II kann nun einen Stein wegnehmen oder zwei. In jedem Fall kann dann Spieler I den letzten Stein nehmen.
Zäumt man das Pferd von hinten auf, so erkennt man die Strategie für den sicheren Gewinn des ersten Spielers: Er muss dafür sorgen, dass er bei seinem letzten Zug genau drei Steine zur Verfügung hat. Dieses Ziel kann er erreichen, wenn er immer – sobald er an der Reihe ist – so viele Steine wegnimmt, dass ein Vielfaches von drei Steinen liegen bleibt und das ist durch die Spielregeln gesichert.
Auch beim nächsten Spiel besteht eine Gewinnstrategie für den Ersten, mit der er immer gewinnen kann, wenn er keinen Fehler macht. Dabei ist die Eigenschaft einer Zahl, gerade oder ungerade zu sein, die Grundlage. Seine Spielregeln sind die folgenden: Zunächst werden die roten Herzchen irgendwie auf die beiden Schalen (=Deckel und Boden des Behälters der Herzchen) verteilt.

Dann beginnt der Erste mit seiner Runde: Er nimmt erstens alle Herzchen aus einer der beiden Schalen und legt sie beiseite. Zweitens verteilt er die Herzchen der anderen Schale irgendwie auf beide Schalen, wobei sich in jeder Schale mindestens ein Herzchen befinden muss. Dann macht der Zweite mit diesen beiden Schalen die gleichen beiden Aufgaben, d.h. er leert eines der beiden Kästchen vollständig und verteilt dann den Inhalt des anderen Kästchens so auf beide Kästchen, dass keines leer ist. Und so weiter, und so weiter. Gewonnen hat derjenige Spieler, der als letzter seine beiden Aufgabenschritte ausführen kann.
Hier ein Beispiel eines kurzen Spielverlaufs:
Beginn eines Spiels mit insgesamt 13 Herzchen, aufgeteilt in sieben und sechs Herzchen auf die beiden Kästchen

Der erste Spieler leert die linke Schale und verteilt den Inhalt der zweiten Schale auf beide:


Der zweite Spieler leert die rechte Schale und verteilt den Inhalt der zweiten folgendermaßen:


Jetzt leert der erste Spieler die rechte Schale und verteilt den Inhalt der linken:


Damit hat er die Partie gewonnen. Der zweite Spieler kann zwar noch eine Schale von zweien leeren, aber nicht mehr den Inhalt der zweiten Schale danach noch regelgerecht “ohne Herzeleid” aufteilen:

Zufall oder Strategie?
Das kurze Beispiel zeigt, warum der erste Spieler hier gewinnen musste, und zwar egal, was der Zweite machte oder hätte machen können.
Bei Beginn lagen in einer Schale eine ungerade und in der anderen eine gerade Anzahl roter Herzchen (7+6=13). Tatsächlich ist bei einer ungeraden Gesamtzahl immer in einer der beiden Schalen eine ungerade Anzahl. Die Summe zweier gerader Zahlen ist immer gerade! Der Erste leert die Schale mit der ungeraden Anzahl Herzchen und teilt die gerade Anzahl der zweiten Schale in eine ungerade und eine gerade Zahl auf die beiden Schalen. Das ist immer möglich. Erst mit der Eins ist kein Weiterspiel mehr möglich. Und der Erste hat das Spiel für sich entschieden.
Nimmt man alle 53 (oder eine andere Teilmenge, die eine ungerade Anzahl besitzt) Herzchen, kann der “Checker” dem “Loser” sogar die Verteilung auf die beiden Schalen großzügig überlassen, weil die ungerade Gesamtanzahl nicht in eine Summe zweier gerader Zahlen zerlegt werden kann.
Ein weiteres kleines Gewinnspiel für zwei Personen mit einer sicheren Gewinnstrategie für den beginnenden und wissenden Spieler ist das folgende:

Es wird auf diesem Band aus drei Wabenreihen mit einem Stein von zwei Personen gespielt. Die beiden Spieler bewegen den Stein abwechselnd nach rechts (von S nach Z). Dabei darf der Stein immer nur auf eine der drei benachbarten Waben bewegt werden. Gewonnen hat derjenige Spieler, der den Stein auf die Wabe mit dem Z bewegen kann.
Es beginnt der erste Spieler, der die Gewinnstrategie kennt, mit dem ersten Zug. Dann folgen in dem teilweise wiedergegebenen Spiel die Schritte 2 und drei.



Beim 4. Schritt muss der zweite Spieler auf eine benachbarte Wabe mit einem dunkelblauen Punkt ziehen. Im darauffolgenden Schritt kann der erste Spieler wieder auf eine Wabe mit einem hellblauen Punkt ziehen usw.
Zeigen wir noch die Schritte 10 bis 13.

Schritt 10 – Spieler 2



Im 13. Schritt zwingt Spieler 1, indem er auf die hellblaue Wabe zieht, den Gegner mit dem nächsten Zug auf eine dunkelblaue Wabe zu ziehen und gewinnt dadurch das Spiel:


Natürlich ist dieses Spiel sinnlos, wenn beide Spieler diese Gewinnstrategie kennen, wie häufig bei Spielen mit sicherer Gewinnstrategie.
Solche Aufgabenspiele mit einer sicheren Gewinnstrategie haben einen sehr direkten Zusammenhang mit mathematischen Aufgabenstellungen: Klare Aufgabenstellung, streng logisches Vorgehen und überzeugende Argumentation der Gewinnstrategie. Damit ist die intellektuelle Seite der Aufgabe eigentlich erledigt. Was nun reizt, ist sein sicheres Wissen bei einem nicht informierten Mitspieler einzusetzen und dessen fragendes Staunen zu wecken, um ihn dann durch eine nicht widerlegbare mathematische Argumentation zweifelsfrei zu überzeugen.
Natürlich gibt es auch solche Strategiespiele mit einer sicheren Gewinnstrategie für den zweiten Spieler.