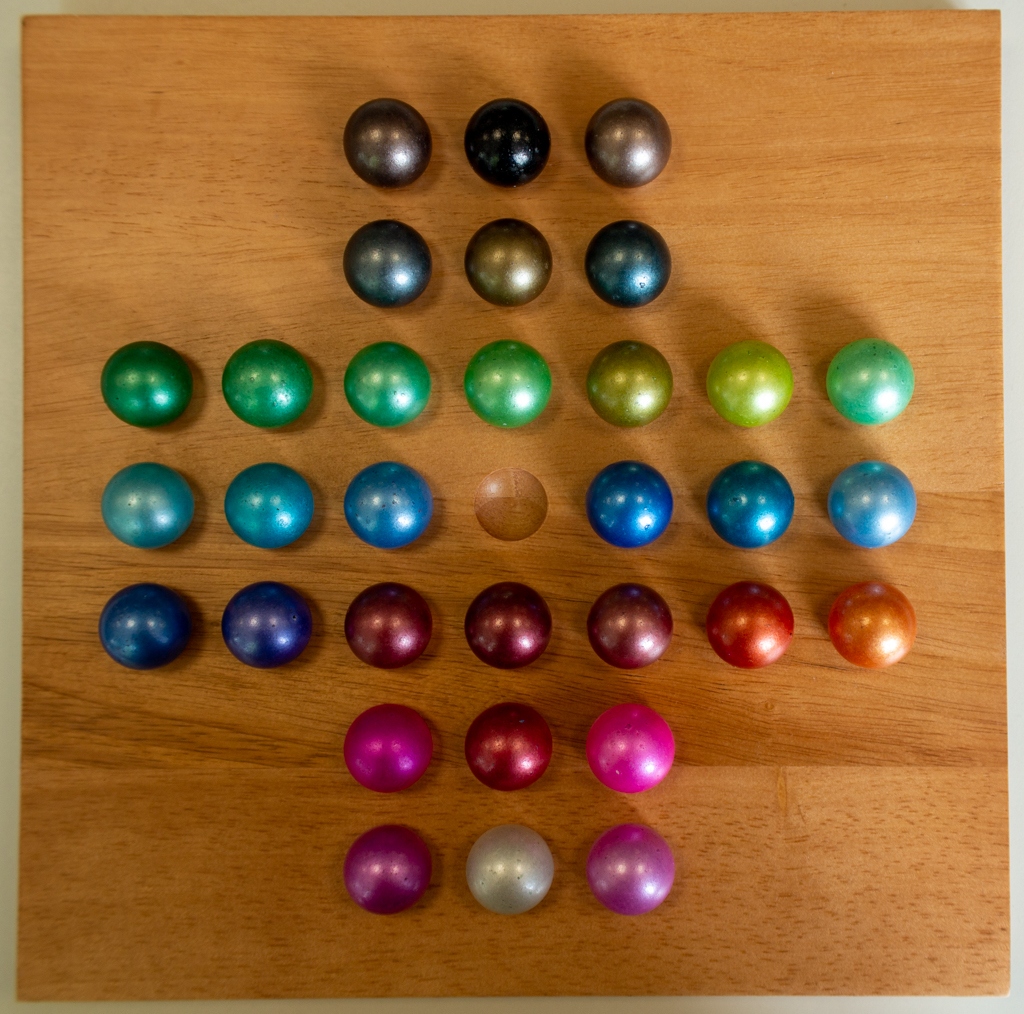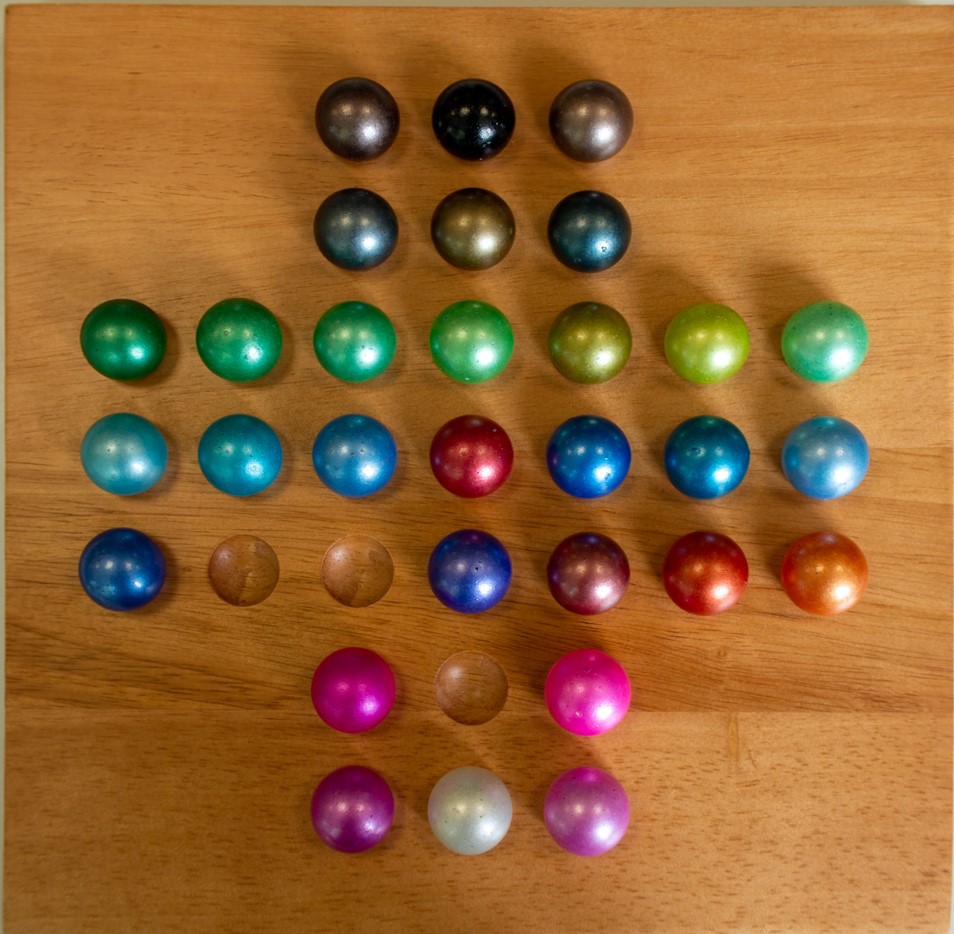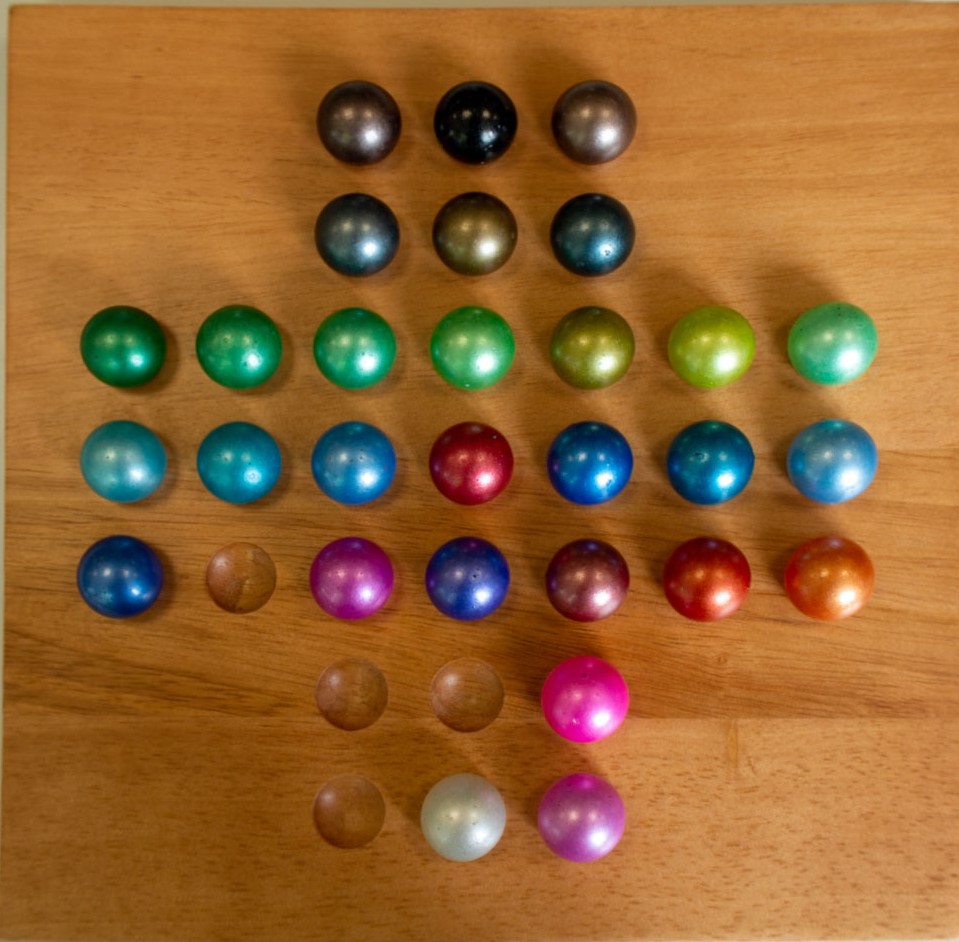Viele Menschen meinen hier wohl eher, dass diese Beschäftigung mit solchen – doch oft sehr künstlich erscheinenden – Problemstellungen unnütze Zeit- und Energieverschwendung sei. Oder wie es einmal ein Schüler – allerdings in schönster Biebricher Mundart – ausdrückte: “Davon wird das Benzin für mein Mofa auch nicht billiger”.
In der Mathothek gibt es kein Mofa, dafür aber ein großes Angebot an solchen scheinbar nutzlosen Objekten, aber vielseitigen und effektiven Trainingsmöglichkeiten kognitiver und logischer Fähigkeiten auf “sportlicher” Art. So z.B. handelt es sich hier um eine derartige Herausforderung mit den typischen Merkmalen: Ausgangslage, Ziel und erlaubte Operationen.
Das Objekt besteht aus einem Brettchen mit einem 11×5 großen quadratischen und fünf Münzen, zwei DM (=Deutsche Mark) und drei 50-Pfennigmünzen.
Startposition und Zielposition:
Erlaubte Operationen sind gleichzeitige Bewegung zweier benachbarter Münzen, ohne ihre Reihenfolge zu verändern. Die gestellte Aufgabe, die Münzen auf diese Weise von links oben nach rechts unten zu verschieben, ist in vier Schritten ausführbar:
Abgesehen von der Möglichkeit, diese zwei besonders interessanten Münzen der ersten Währung der Bundesrepublik Deutschland betrachten zu können – insbesondere lohnt es sich, die Rückseite des 50-Pfennigstücks zu betrachten und zu deuten – ist dieses Spiel typisch für diese Art Aufgaben. Ein Problem, das im wahren Leben nicht auftritt und dessen Lösung folglich für den Alltag auch keine eindeutige Hilfe verspricht.
Ein sehr verbreitetes Solitärspiel besteht aus einem Brett mit 33 zu einem griechischen Kreuz angeordneten Vertiefungen und 32 Kugeln. Zu Beginn werden die 32 Kugeln auf das Brett verteilt, die Mitte bleibt frei.
Das Ziel des Spiels besteht darin, alle Kugeln zu entfernen, bis auf eine in der Mitte.
Die Kugeln werden entfernt, indem man mit einer Kugel über eine benachbarte auf ein freies Loch dahinter springt und die übersprungene Kugel entfernt. Hier ein Beispiel für die ersten drei möglichen Schritte:
Fortgeschrittene Schritte eines Spiels:
Die letzten drei Schritte:
Viel bekannter und weltweit verbreitet sind solche “nutzlosen” Solitärspiele wie Sudoku und Rubik-Würfel, einschließlich dessen “Kinder und Enkel”.
Zu beiden gibt es in der Mathothek eine Fülle von Beispielen und Varianten:
Es gibt noch viele Angebote für jeden Besucher der Mathothek, der sich mit mathematisch verwandten Aufgaben und Fragen auseinandersetzen möchte, z.B. mit lateinischen und lateinisch-griechischen Quadraten, einem Bereich, der durchaus von bedeutenden Mathematikern beackert worden ist.
Aber auch magische Quadrate und ähnliche Aufgaben können als Solitärspiele mit Zahlen und Rechenregeln dienen:
Rätsel und Aufgabenstellungen, bei denen es um scheinbare oder echte logische Widersprüche und damit auch um unsere Sprache geht, stehen in der Mathothek in sehr attraktiven und anschaulichen Exponaten zur Verfügung:
Viele Angebote der Mathothek bieten auch Möglichkeiten, intellektuelle Anstrengungen mit meditativen Übungen zu verbinden, beispielsweise eine Reihe von Legespielen.
Im Grunde genommen lassen sich, wenn man will, fast alle Experimente der Mathothek auch als “Solitärspiel, Knobelei oder Rätsel” auffassen. Umgekehrt lassen sich viele mathematische Aussagen oder Übungen auch zu Rätseln, Knobelaufgaben und Solitärspielen gestalten. Häufig wird dadurch ein gewisser Widerstand gegen die “nackte” Mathematik überwunden.
Hier soll aber auf keinen Fall das “Solitär” als wesentliches Element irgendwie betont werden. Im Gegenteil! Alle diese Spiele und Experimente sind auch in Kooperation sehr gut zu machen. Das gemeinsame Lösen von Problemstellungen und das gemeinsame Erreichen eines Zieles können erfolgreicher sein und mehr Freude machen als es vielleicht individuelle Bemühungen in Isolation können. Ein schönes Beispiel ist für mich immer wieder das “Spiel” des perfekten Quadrats:
Bisher hat es noch nie ein einzelner Besucher versucht oder gar geschafft, die 21 verschiedenen Quadrate perfekt auf das große Quadrat zu platzieren. Allerdings haben es kleinere Gruppen nach verständlichen Anfangsschwierigkeiten beim Kooperieren nach einiger Zeit immer geschafft: