NIM-Spiele sind spieltheoretisch sehr gut erforschte Spiele und es gibt auch in der Mathothek eine ganze Reihe verschiedener Varianten davon. Dabei sind NIM-Spiele Gewinnspiele für zwei Personen, die abwechselnd von einer Menge von Objekten, z.B. Streichhölzern, Steinchen oder Stäbchen, nach bestimmten Regeln welche wegnehmen. Bei den Standardspielen gewinnt derjenige Spieler, der das letzte Objekt für sich beanspruchen kann. Es gibt aber auch NIM-Spiele (Misère-Variante), bei denen der Spieler verliert, der gezwungen werden kann, das letzte Objekt zu nehmen.
Bei dem folgenden speziellen NIM-Spiel geht es darum, dass die Objekte fünf Hölzchen sind und die beiden Spieler je Zug ein, zwei oder drei Hölzchen entfernen dürfen. Derjenige Spieler, der gezwungen ist, das letzte Hölzchen zu nehmen, verliert das Spiel.
Dieses NIM-Spiel besitzt eine sichere Gewinnstrategie für den zweiten Spieler. Die Rolle des zweiten Spielers übernimmt unser „Computer“, der allerdings einen menschlichen Assistenten benötigt, um dessen Handlungen real auszuführen. Dabei ist es nicht nur möglich, sondern sogar wünschenswert, dass dieser „Computer-Knecht“ keine Ahnung von dem Spiel, seiner Gewinnstrategie und seinem Ziel hat, sondern praktisch nur ganz „stumpfsinnig“, die Anweisungen an den Computer ausführt.
Und das hier ist unser „lernender Computer“:
Ausgepackt und startklar, sieht unsere Learning Machine dann so aus:
Es folgen jetzt die Protokolle dreier Spiele, Mensch (M) gegen Maschine (C). Vor Spielbeginn werden in jedes der drei Rest-Kästchen (Rest IIII, Rest III und Rest II) je drei Karten mit den drei Symbolen – Kreis, Dreieck und Quadrat – gelegt. Das geschieht jeweils in beliebiger Reihenfolge und des Effektes wegen auch verdeckt. Diese drei Symbole sind auch auf den drei Computer-Anweisungen zu finden, auf denen der Computer angewiesen wird, welche Anzahl Hölzchen er nehmen soll. Danach ist der Computer startklar.
Erstes Match:
M nimmt in der ersten Runde ein Hölzchen. C ermittelt die Zahl der verbliebenen Hölzchen, also den Rest IIII.
C nimmt die oberste Karte aus „Rest IIII“, ein schwarzes Dreieck und erhält so den Befehl: Nimm 2!
C nimmt zwei Hölzchen. Anschließend nimmt M davon eines und zwingt so, C das letzte Hölzchen zu nehmen. Die Karte mit der zum Verlieren führenden Anweisung wird aus dem Kästchen Rest IIII entfernt
Zweites Match:
Wieder liegen fünf Hölzchen bereit, aber die Unglückskarte aus der ersten Runde ist nicht mehr im Spiel, d.h. der Computer kann diesen Fehler nicht mehr machen, er hat gelernt.
Diesmal nimmt M zwei Hölzchen. C bestimmt den Rest III und erhält die Anweisung: Nimm 2! Somit zwingt er M, das letzte Hölzchen zu nehmen. C hat diese Runde gewonnen. Die Karte mit der erfolgreichen Anweisung wird in das Rest III-Kästchen als unterste zurückgelegt. Wieder hat die Maschine einen Lernschritt gemacht.
Alles ist bereit für das dritte Match:
Wieder sind alle fünf Hölzchen im Spiel und M nimmt als Anfänger diesmal wieder zwei. C erhält diesmal die Anweisung: Nimm 1! Es bleiben dann für M noch zwei Hölzchen und damit lässt er die Maschine verlieren. Der Gewinn für den Computer besteht natürlich darin, dass die unglückliche Anweisung entsorgt wird und er so diesen Fehler nicht wiederholen kann.
Wenn man mithilfe der korrekten Ablage der Anweisungskarten alle möglichen neun verschiedenen Spiele durchgespielt hat, darunter sechs von C verlorenen und drei von C gewonnen Spielen, wird die Maschine bei jedem weiteren Spiel immer der Sieger und der Mensch der Verlierer sein.
Wie sieht der Endzustand unseres ausgelernten und nun immer siegreichen Computers aus?
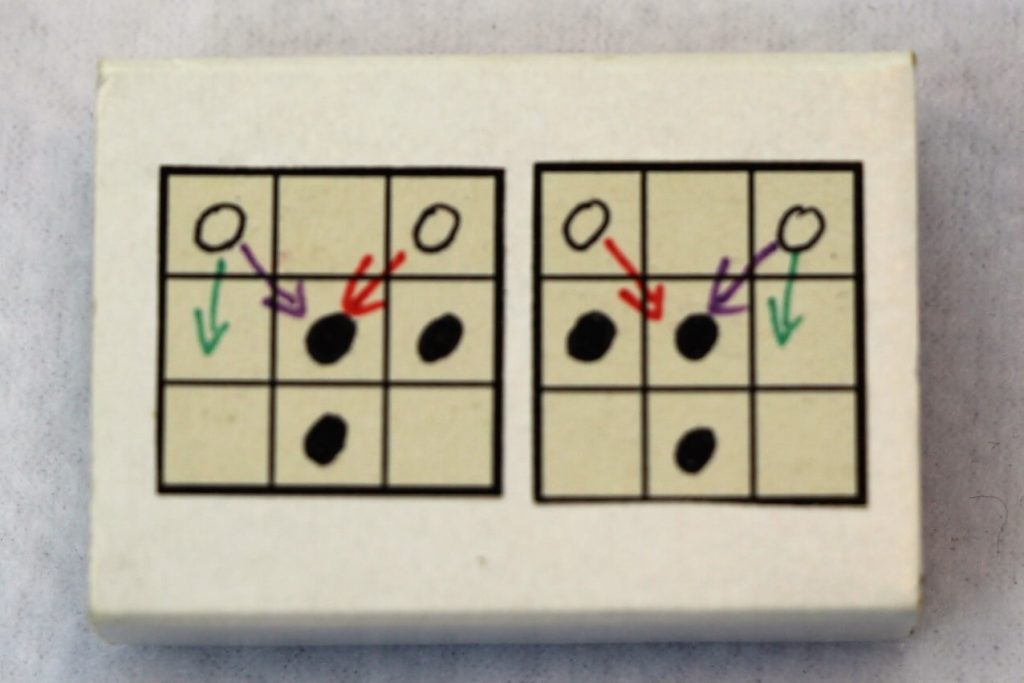
In jedem der drei Rest-Kästchen liegt nun – allerdings zunächst noch verdeckt – nur noch eine Computer-Anweisung und diese und nur sie führt zum Gewinn für C:
Damit ist es nun nicht schwierig, die Gewinnstrategie für den zweiten Spieler zu formulieren:
Nimmt der erste Spieler 1 Objekt, so nimmt der zweite 3,
nimmt der erste Spieler 2 Objekte, so nimmt der zweite auch 2,
nimmt der erste Spieler 3 Objekte, so nimmt der zweite 1 Objekt.
In der Mathothek gibt es einen weiteren lernenden Computer – und eine ausführliche Beschreibung im Katalog – , der etwas aufwendiger ist und sich auf ein Bauernschach, eine sehr reduzierte Variante von Schach, bezieht. Auch hier liegt eine vollständige Analyse des Spiels und eine sichere Gewinnstrategie für den zweiten Spieler vor. Mit jedem Spiel wird der Computer besser, um schließlich dem menschlichen Gegenspieler keine Gewinnchance mehr zu geben.
Auch wenn mit diesen beiden kleinen Experimenten der Weg zur derzeit sich explosionsartig entwickelnden KI natürlich noch riesig und aus verschiedenen Gründen nicht vollständig nachvollziehbar ist, vermitteln die beiden einfachen Exponate doch gute erste Einblicke in das Grundverständnis der Lernprozesse bei Maschinen und Computern.