Im 17. Jahrhundert wettete Prinz Ruprecht von der Pfalz, dass man einen Würfel durch einen Würfel derselben Größe hindurchschieben könne. Also genauer, dass man in einen Würfel ein Loch machen könne, durch das sich dann ein zweiter Würfel mit derselben Größe hindurch bewegen ließe. Da er die Wette gewann, bezeichnet man heute einen Würfel mit einem solchen Loch als Prinz-Ruprecht-Würfel.
Es gibt aber noch ein zweites Exponat, das etwas handfester und für Interaktionen geeigneter ist:
Um sich eine Vorstellung davon zu machen, wie das passende Loch in dem Prinz-Ruprecht-Würfel ausgehöhlt werden muss, gibt es einige kleinere Objekte zu experimentieren. Sie sind alle durch Querschnitte in gleich große Holzwürfel entstanden. Die beiden ersten Versuche, den Würfel jeweils in zwei gleiche Teilkörper zu zerlegen sind simpel und helfen nicht weiter:
Zwar ist die Schnittfläche im Falle der Diagonalschnitte bereits größer als das Quadrat im ersten Versuch, aber nicht groß genug für ein geeignetes Loch. Eine größere Schnittfläche liefert erst der dritte Versuch, den Würfel zu halbieren. Dieses Mal legen wir die Schnittebene so an, dass sie alle Kanten des Würfels in der Mitte schneidet. Die Schnittfläche ist dann ein regelmäßiges Sechseck, das flächenmäßig größer als das Quadrat jeder Seitenfläche des Würfels ist:
Mit einer kleinen Schlinge aus Gummikordel kann man die Schnittflächen, die durch alle sechs Kanten des Würfels gehen, variieren.
Projiziert man einen Würfel – hier das Ergebnis für den großen, transparenten Würfel – parallel zu einer seiner diagonalen Achsen, so ist das Ergebnis ein regelmäßiges Sechseck:
Tatsächlich führt diese Überlegung zur genialen Lösung der gestellten Aufgabe, wie man an den folgenden Bildern erkennen kann:
In der Mathothek gibt es bei einer kleinen, aber feinen Sammlung von Modellen von Durchdringungen von geometrischen Körpern aus Pappe einen solchen Prinz-Ruprecht-Würfel:
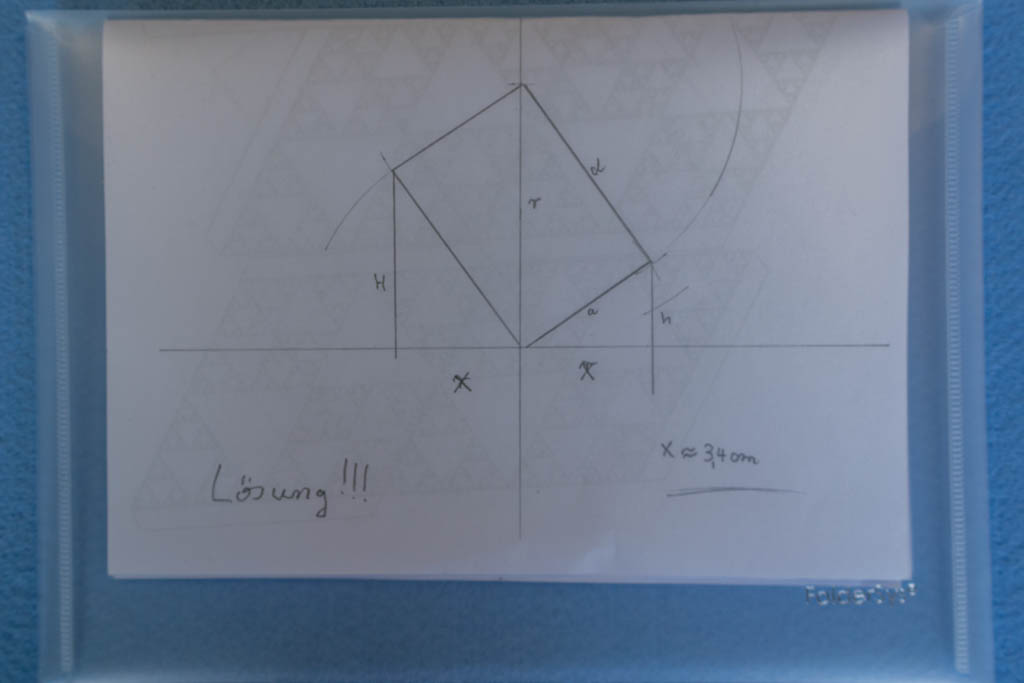
Für diejenigen unter Euch, die wissen wollen, wie man die oben gezeigte Parallelprojektion konstruieren kann, gibt es das originale Zeichenblatt in einem transparenten Briefumschlag zum Nachvollziehen:
Dazu vergleiche auch die drei kleinen Objekte, die über den Zusammenhang von Kantenlänge, Seiten- und Raumdiagonale des Würfels die Konstruktion verständlich machen: