Was bedeutet in der Mathematik, eine gekrümmte Linie zu messen? Die Messung erfolgt dadurch, dass man die Kurve zunächst durch einen Streckenzug ersetzt und dann die Länge des Streckenzugs als Annäherung (=Approximation) an die Länge der gekrümmten Linie nimmt.
Wir betrachten die folgende Kurve als Beispiel:
Wir benutzen zunächst zwei verschiedene Zollstäbe. Einer hat 20cm lange Glieder und der zweite 10cm lange.
Im ersten Fall erhalten wir als Ergebnis 32cm und im zweiten sind es 58cm. Natürlich sehen wir, ohne überrascht zu sein, dass die erste Näherung sehr ungünstig und zweite Näherung wesentlich größer als die erste ist und damit die genauere Annäherung an die “wahre” Länge der Kurve darstellt.
Beim zweiten Anlauf benutzen wir einen Stechzirkel mit drei verschiedenen Öffnungen: 10cm, 5cm und 1cm.
Bei 10cm großen Schritten erhalten wir 5⋅10cm=50cm, bei 5cm großen Schritten 12⋅5cm=60cm und mit der kleinsten Öffnung von 1cm bekommen wir 1⋅64cm=64cm.
Das Experiment überrascht natürlich nicht wirklich. Es bestätigt aber, dass die Ergebnisse größer werden (oder gleich bleiben), je kleiner die Schritte werden. Wir machen noch zwei Versuche, das eine Mal benutzen wir Ketten mit Kugeln, die einen Durchmesser von 16mm, 8mm bzw. 4mm haben.
Die Ergebnisse liefern bei 16mm Durchmesser 40 Perlen, bei 8mm 83 und bei 4mm 173 Perlen, d.h. wir erhalten die Längen 64cm, 66,4cm und 69,2cm.
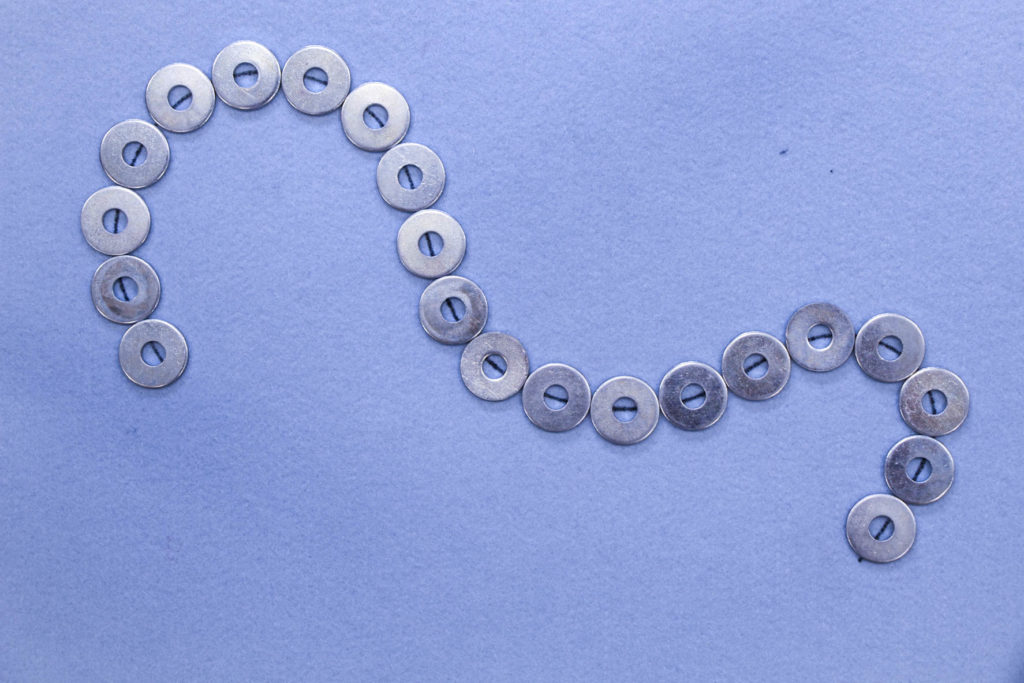
Beim zweiten Versuch nehmen wir Unterlegscheiben mit Durchmessern von 30mm und 20mm.
Im Falle der Unterlegscheiben mit 30mm Durchmesser erhalten wir 21 Scheiben und bei 20mm 32 Scheiben, also bekommen wir 63cm und 64cm als Messergebnisse. Nichts Verwunderliches! Wer Lust hat kann gerne auch mithilfe der Scheiben mit 10mm messen.
Anschaulich ist uns klar, dass diese Annäherungen an die Länge einer gekrümmten Linie mithilfe von Streckenzügen sich mit zunehmender Feinheit (immer kürzere Teilstrecken) einem Grenzwert näheren, der dann die Länge der Kurve darstellt. Das gilt auch für die Länge einer Kreislinie, deren Länge 2⋅Radius⋅π beträgt und durch eine Folge von Streckenzügen in Form von regelmäßigen Vielecken ermittelt werden kann.
Gibt es nun auch eine einfache geschlossene Kurve, deren Länge unendlich ist, obwohl der Inhalt der von ihr eingeschlossenen Flächen endlich ist?
Dass es eine solche Figur gibt, beweist die sog. Koch’sche Schneeflockenkurve:
Wie sieht es nun mit dieser interessanten fraktalen Figur aus? Sie ist als Koch’sche Schneeflockenkurve bekannt. Dabei zeigt die obige Figur nur die ersten vier Schritte zu der eigentlichen Schneeflockenkurve, die das Grenzprodukt von unendlich vielen weiteren Schritten dieser fraktalen Figur ist. Umfänge und Flächeninhalte der einzelnen schrittweise entstehenden Figuren lassen sich relativ einfach berechnen. Dabei ist sofort einzusehen, dass mit jedem Schritt die neue Figur hinsichtlich Umfang und Inhalt größer ist als die vorhergehende. Allerdings besitzt nur die Folge der Inhalte einen endlichen Grenzwert. Die Folge der Inhalte der einzelnen Schritte ist zwar wachsend, aber auch beschränkt, z.B. können diese Werte nicht größer werden als die Fläche des gelben Quadrats. Die Länge des Umfangs der Schneeflockenkurve ist jedoch unendlich, weil die Folge der Umfänge der einzelnen Figuren über jede Schranke wächst.
Von der zweiten Behauptung kann man sich überzeugen, indem man den schrittweisen Aufbau der Schneeflockenkurve benutzt. Dann überlegt man sich, dass bei jedem Schritt der Umfang der Schneeflocke um 1/3 wächst, also 4/3 des Umfangs der vorhergehenden Schneeflocke beträgt. Wenn also der Umfang des Ausgangsdreiecks 3(=3⋅1) ist, dann sind die Umfänge der nächsten Schneeflocken (4/3)⋅3(=4), (4/3)⋅(4/3)⋅3(=5,3…) und (4/3)⋅(4/3)⋅(4/3)⋅3(=7,1…) usw. Die n-te Schneeflocke hat dann den Umfang (4/3)n⋅3 . Die Exponentialfunktion x→(4/3)x wächst über jede noch so große Zahl, d.h. die Koch’sche Schneeflockenkurve ist unendlich lang.
In der Mathematik dient diese Koch’sche Schneeflockenkurve als Beispiel für eine Kurve, die zwar überall stetig, aber nirgends differenzierbar ist. Hier zeigt das Beispiel der Koch’schen Schneeflockenkurve, dass es Kurven gibt, die einen begrenzten Flächeninhalt einschließen, aber selbst keine endliche Länge besitzen.
In der aufkommenden Chaostheorie, die sich intensiv mit Fraktalen beschäftigt, stellte sich die Frage nach der Länge einer Küste, z.B. der Küstenlänge Großbritanniens. Klar ist, dass die Messergebnisse mit jedem feineren Grundmaß wächst, da man schließlich jede Einbuchtung und jeden Vorsprung einbeziehen muss, schließlich auch Steine, Kiesel, Sand usw. Wie wir am Beispiel der Koch’schen Schneeflockenkurve sehen können, reicht das Wissen über die Endlichkeit der Flächengröße Großbritanniens für die Endlichkeit der Kurvenlänge der Küstenlinie nicht aus.