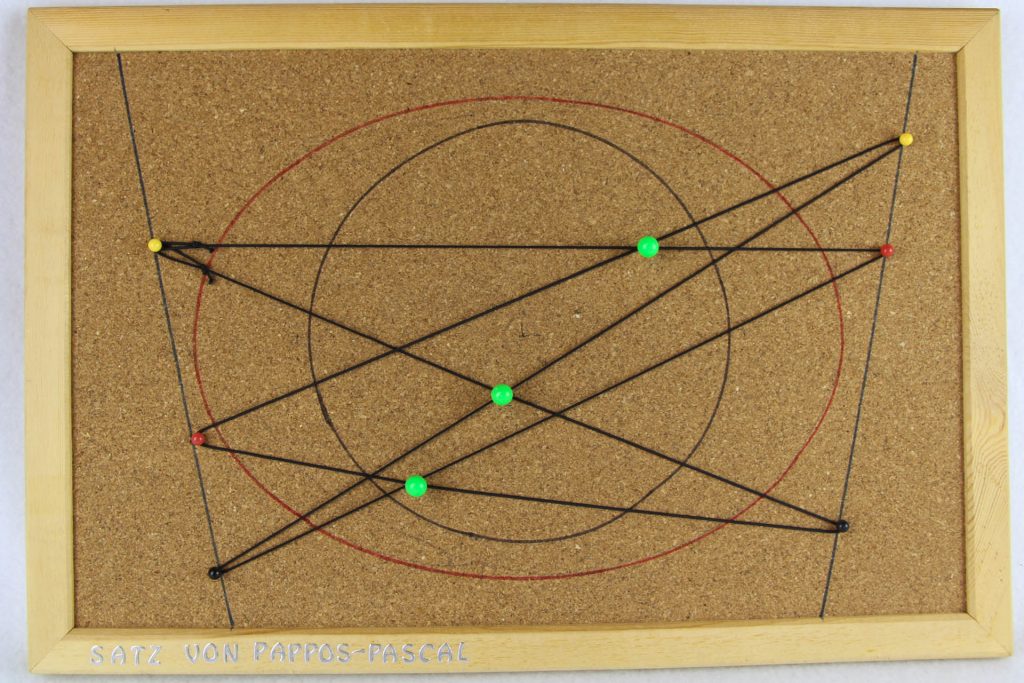
In der Mathothek gibt es ein Exponat, mit dem man einen bereits in der griechischen Antike bekannten und formulierten Satz anschaulich klarmachen kann.
Auf der Korkplatte befinden sich aufgemalt zwei nicht-parallele Geraden, eine Ellipse und ein Kreis. Dazu gibt es einen schwarzen Gummifaden und Pinnnadeln.
Wählt und fixiert man auf jeder der beiden Geraden je drei Punkte, die dann in der angegebenen Reihenfolge, d.h. abwechselnd, mit dem Gummifaden verbunden werden, so kommt man zu folgender richtigen Vermutung: Die drei mit grünen Pinnnadeln markierten Schnittpunkte liegen auf einer Geraden:
Die drei Schnittpunkte sind die Schnittpunkte der jeweils zwei gradlinigen Verbindungen der gelben und roten Punkte, der gelben und schwarzen Punkte sowie der beiden roten und schwarzen Punkte.
Natürlich ist dieses Experiment und die beschriebenen Beobachtungen noch kein Beweis, der nur auf der Grundlage der Axiome der Geometrie und den streng definierten Voraussetzungen des Satzes von Pappos logisch hergeleitet werden muss. Dieser richtige Satz der Geometrie lässt sich auch so formulieren: “Liegen die Eckpunkte eines Sechsecks abwechselnd auf zwei beliebigen Geraden, so sind die Schnittpunkte der gegenüber liegenden Seiten des Sechsecks kollinear, d.h. sie liegen auf einer Geraden.”
Wer Lust und Spaß daran hat, kann dieses Experiment mit den beiden Geraden auf einen Kreis und auch auf eine Ellipse übertragen, indem er die sechs Punkte entsprechend auf dem Kreis bzw. der Ellipse wählt und markiert. Auch in diesen beiden Fällen liegen die entsprechenden Schnittpunkte jeweils auf einer Geraden.
Das hat ca. 1200 Jahre später der französische Mathematiker Blaise Pascal entdeckt. Erfand heraus, dass der Satz von Pappos nicht nur für zwei beliebige Geraden, sondern auch für Kreis, Ellipse und Hyperbel, d.h. für alle Kegelschnitte Gültigkeit besitzt. So heißt die zusammengefasste wahre mathematische Aussage nach beiden großen Mathematikern heute der Satz von Pappos-Pascal:
“Ist ein Sechseck einem Kegelschnitt eingeschrieben, so sind die Schnittpunkte gegenüberliegender Seiten kollinear, d.h. sie liegen auf einer Geraden.”
Pappos von Alexandrien lebte im 4. Jahrhundert in Alexandria und war der letzte große Mathematiker und Astronom der Antike. Blaise Pascal (1623 bis 1662) war ein französischer Mathematiker, Physiker, Literat und christlicher Philosoph. In der Mathematik ist das “Pascal’sche Dreieck” nach ihm benannt, ein mathematisch hochinteressantes Zahlendreieck, das einen sehr einfach zu beschreibenden Aufbau besitzt, aber eine Fülle mathematischer Eigenschaften in sich birgt.