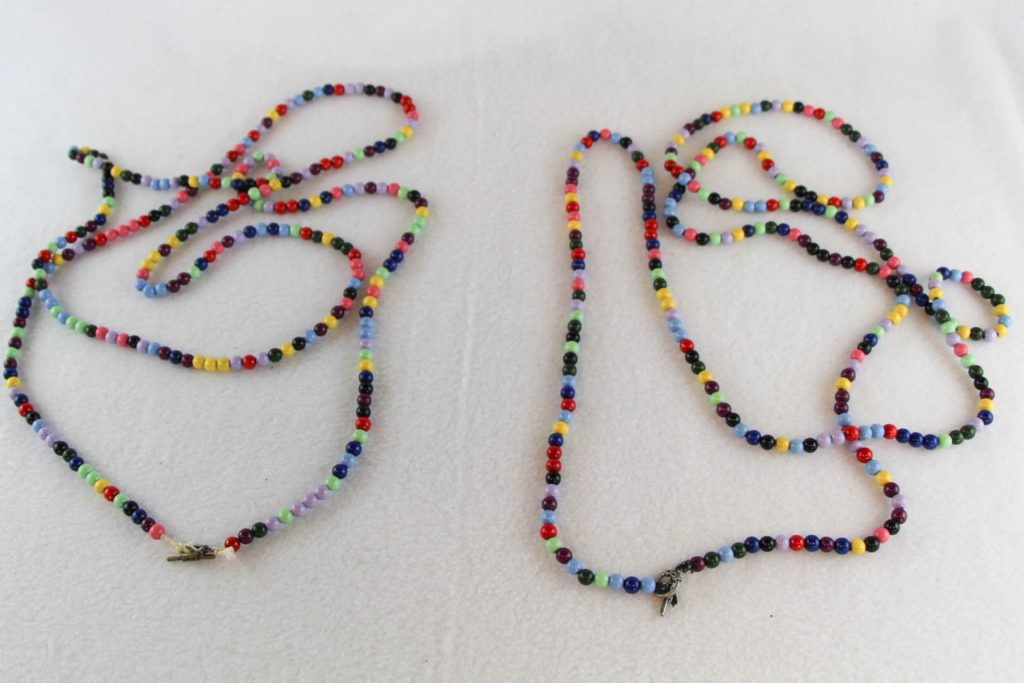Eine der interessantesten Zahlen in der Mathematik ist die Kreiszahl π, die meist als π≈3,14 zur Berechnung des Flächeninhalts A=π⋅r2 und des Umfangs U=π⋅2r eines Kreises allgemein bekannt ist. Für Mathematiker scheint diese Zahl eher ein Brunnen ohne Boden zu sein. Um ein wenig davon zu zeigen, entstanden in der Mathothek eine Reihe von Exponaten und Experimenten. So auch eine Perlenkette („Pi-Kette“), bei der Perlen zehn verschiedener Farben für die Ziffern 0 bis 9 eingefädelt wurden, und zwar sodass die Farben der Perlen den Anfang der Ziffernfolge von π widerspiegeln. Für eine zweite Kette wurden Perlen mit denselben zehn Farben rein zufällig hintereinander eingefädelt, sodass eine rein zufällige Ziffernfolge entstand:
Die Ähnlichkeit der beiden Perlenketten ist nicht zu übersehen.
Nach dieser Einleitung ist es vielleicht nicht völlig überraschend, dass die folgende „Perlenkette in Schwarz und Weiß“ auch etwas mit der Zahl Pi etwas zu tun haben könnte. Da es nur zwei Farben gibt, könnte es sich um die Ziffern 0 und 1 handeln. Es sind tatsächlich die ersten acht Ziffern von der binären Darstellung von π. Die binäre oder auch duale Darstellung der Zahlen ist die Form, in der Computer mit den Zahlen rechnen. Durch Ausprobieren findet man schnell heraus, dass eine schwarze Perle für 1 und eine weiße für 0 stehen und nach den beiden schwarzen Kugeln ein Komma stehen muss:
s s, w w s w w s entspricht dann 11,001001 im Binärsystem, also um die betreffende Zahl 1⋅21+1⋅20+0⋅2-1+0⋅2-2+1⋅2-3+0⋅2-4+0⋅2-5+1⋅2-6 im Dezimalsystem, d.h. 2+1+0+0+0,125+0+0+0,015625=3,140625. Es also ein Näherungswert für π. Wie sieht aber der umgekehrte Weg aus, nämlich wie findet man aus der dezimalen Darstellung von π die entsprechende binäre? Dafür gibt es ein besonderes Objekt in der Mathothek:
Durch schrittweises Umwenden der vier oberen Leistchen kommt man dann zur gesuchten Lösung und zur Erkenntnis eines geeigneten Algorithmus, mit dem sich dann pi aus der dezimalen Darstellung auf beliebig viele binäre Nachkommastellen berechnen lässt.
Als Erstes brauchen wir die Basis- oder Grundzahlen des Binärsystems:
Danach verwandeln wir diese Grundzahlen in ihre Dezimalschreibweise:
Im nächsten Schritt addieren wir von links nach rechts jeweils so, dass bei jedem Schritt die neue Summe gerade noch kleiner als π ist. Würden wir die betreffende Zahl nämlich doch noch zu unserem Zwischenergebnis addieren, könnte unser Verfahren nicht mehr zu π führen, weil immer nur null oder eine positive Zahl addiert wird,
Auf diese Weise erhält man eine Folge von Zahlen, die monoton wächst und sich immer mehr in unendlich vielen Schritten der Kreiszahl π nähert.
Schreiben wir nun eine 1 für den Fall, dass wir die entsprechende binäre Grundzahl addieren und eine 0, wenn wir es nicht tun, so erhalten wir die gewünschte binäre Annäherung an Pi: 11,001001
Mit der Hilfe eines Taschenrechners oder natürlich eines Computers lässt sich dieser Algorithmus auch für genauere Annäherungen an π durchführen und dann „mathothekisch“ das Ergebnis auch in eine Kette mit schwarzen und weißen Perlen verwandeln, deren „tiefere“ Botschaft wohl die meisten nicht Eingeweihten noch nicht einmal ahnen werden:
Eine solche längere Pi-Kette mit 31 schwarzen bzw. weißen Perlen, die es in der Mathothek gibt, stellt die Zahl π mit 29 Nachkommastellen im Binärsystem dar:
π=11,00100100001111110110101010001… .
In der Mathothek gibt es noch eine größere Anzahl an Schmuckketten, die ebenfalls solche versteckten mathematischen Wahrheiten in sich tragen. Vielleicht macht es Dir ja Spaß, sie zu entschlüsseln oder auch selber welche auszudenken.