Ein solch faszinierendes Buch, das ebenso mathematisch ist wie künstlerisch, lässt sich in der Mathothek entdecken und genießen. Es ist der Katalog zu einer Wanderausstellung vom Anfang des 3. Jahrtausends, die auch im Mathematikum in Gießen zu sehen war. Sie zeigte Arbeiten des Ingenieurs und Künstlers Franz Xaver Lutz, von dem auch die Texte des Katalogs stammen. Alle Bilder haben einen mathematisch-geometrischen Inhalt, wie in einem ansprechenden Mathematikbuch. Aber anders als in einer rein mathematischen Darstellung wird das Bild in seiner Ganzheit zu einem faszinierenden Kunstwerk. Franz Xaver Lutz lässt sich von Formen, die er in Natur und Technik findet, inspirieren und schlägt dann die Brücke zu ihrer exakten mathematischen Darstellung. Auf diese Weise spricht er sowohl den Kunstliebhaber als auch den Mathematiker an und schafft so eine Brücke zwischen den zwei “Kulturen”.
Ich denke, dass Kunst und Mathematik in vielerlei Hinsicht unterschiedlich daran gehen, die Welt zu erkennen und zu den Fundamenten von Wahrheit und Schönheit vorzudringen. Dabei unterscheiden sich natürlich ihre Wege, Mittel und Methoden. Gemeinsam sind ihnen allemal die Sprache, der Ausdruck und die Darstellung. Geht es in der Kunst oft um Metaphern, Symbole und Bilder, mit denen aus Sicht der Mathematiker zu viel Assoziationen und vage Inhalte verbunden sind, so ringen sie selbst um genau bestimmende Definitionen, missbilligen sie jeden Rückgriff auf die Anschaulichkeit und akzeptieren nur die reine Logik als Richterin auf der Wahrheitssuche. Dagegen finden viele Künstler diese Beschränkungen und die angestrebte Reduktion und Abstraktheit oft als lebensfern und leer.
Andererseits gibt es wohl schon seit ihren Anfängen wesentliche Parallelen zwischen der Kunst und der Mathematik. So versuchten die Menschen mit diesen beiden kulturellen Bestrebungen aus ihrem bloßen Ausgeliefertsein an die Natur schrittweise ein wenig herauszutreten. Im alten Mesopotamien und Ägypten und schließlich in der Entwicklung der griechischen Kultur, Kunst und Mathematik auf einem Höhepunkt ihrer Entwicklung alles andere als Gegner. Spätestens in der Renaissance befruchteten sich die beiden ungleichen Kulturen in einem neuen Höhepunkt. Maler und Bildhauer waren meist auch gute Mathematiker und Geometer. Durch die Erkenntnis der Perspektivgesetze gelang z.B. eine bisher nicht gekannte räumliche Darstellung in der Kunst. Die Entdeckung des Goldenen Schnitts beförderte die bessere Wahrnehmung und die Darstellung von Proportionen und Harmonie in der Kunst.
Seit den Anfängen der modernen Kunst um die Zeit des Beginns des 20. Jahrhunderts begann eine neue Ära fruchtbarer Auseinandersetzung der Kunst mit der Geometrie und der Mathematik allgemein. Als wesentliches Beispiel sei hier nur der niederländische Maler Piet Mondrian genannt, der auf seiner Suche nach den Fundamenten der Schönheit und Wahrheit zunehmend den Weg zur abstrakt-geometrischen Kunst beschritt.
In der Mathothek gibt es eine Fülle von Exponaten, die sich mit vielen Aspekten von Trennendem und besonders von Verbindendem zwischen Mathematik und Kunst beschäftigen. Gemeinsam geht es in der Kunst und der Mathematik um die Auseinandersetzung mit der Natur und der Realität auf der Suche nach der zeitlosen und fundamentalen Schönheit und Wahrheit. Dabei lassen sich viele Künstlerinnen und Künstler gerade durch die Mathematik mit ihren ewig gültigen Aussagen herausfordern.
Ich sehe vor allem drei Ansätze zur Annäherung und Verbindung der Kunst mit der Mathematik:
- So führt die Verwendung von geometrischen Erkenntnissen und Aussagen, wie die Gesetze der Perspektive oder der goldene Schnitt zur realistischeren und harmonischeren Gestaltung ihrer Werke
- Der Weg über die Reduktion der Natur und der Verzicht auf subjektive und emotionale Details führt zur angestrebten Objektivität von fundamentaler Schönheit und Wahrheit der abstrakt-geometrischen Malerei
- Von der Faszination an der Mathematik mit ihren logisch aus wenigen Axiomen objektiv gewonnen und unbegrenzt gültigen Aussagen lässt sich die Kunst in ihrem eigenen Bestreben herausfordern und beflügeln
Andererseits haben viele Mathematiker auch tiefes Interesse an der Kunst, sowohl an der bildnerischen wie der musikalischen.
Der Katalog von Franz Xaver Lutz zitiert einige Aussagen zur Beziehung von Kunst und Mathematik von berühmten Mathematikern und Künstlern. Sie geben mit einigen pointierten Formulierungen ein Bild von den beiden Kulturen und ihrem Verhältnis zueinander:
- “Die Mathematik, recht betrachtet, besitzt nicht nur Wahrheit, sondern auch höchste Schönheit – eine kalte und strenge Schönheit gleich einer Skulptur, ohne Anziehungskraft für irgendeine unserer schwächeren Seiten, ohne die prächtigen Anreize der Malerei oder Musik, aber von erhabener Reinheit und einer strengen Vollendung, wie sie nur höchste Kunst aufweisen kann.” (BERTRAND RUSSELL, britischer Philosoph und Mathematiker, 1872-1970)
- “Wer die Welt verstehen will, in der wir heute leben, muss die Sprache des Mathematikers wenigstens in ihren Grundzügen beherrschen.“(HERBERT MESCHKOWSKI, Mathematiker,1909-1990)
- “Die Werke des Mathematikers müssen schön sein wie die des Malers oder Dichters; die Ideen müssen harmonieren wie die Farben der Worte. Schönheit ist die erste Prüfung: Es gibt in der Welt keinen Platz für hässliche Mathematik.” (GODFREY HAROLD HARDY, Mathematiker, 1877-1950)
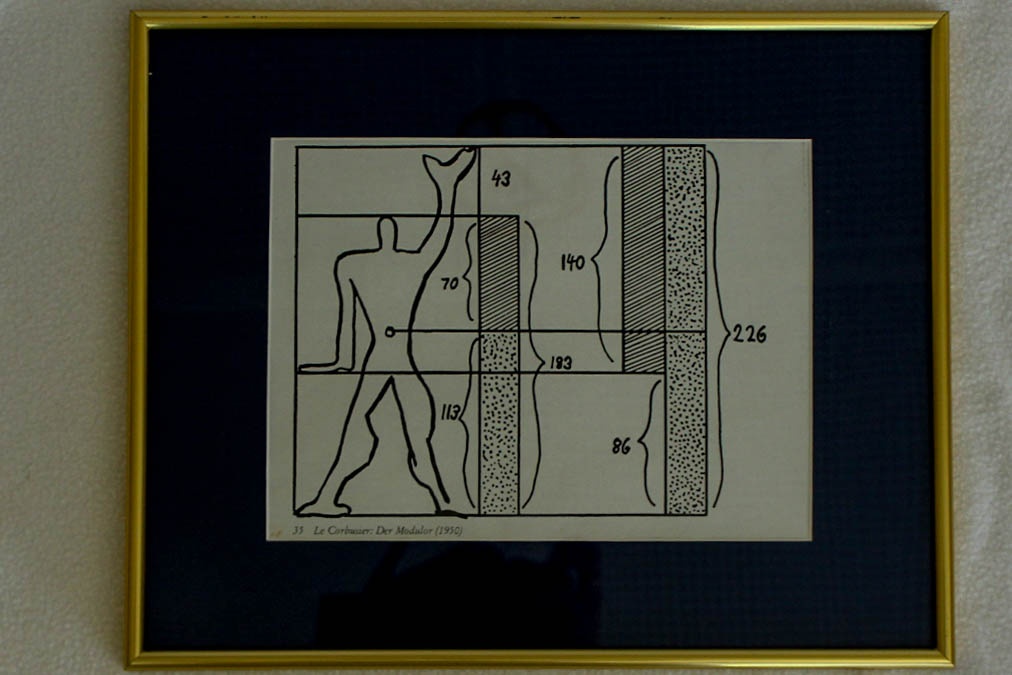
- “Die mathematischen Wissenschaften sind der Meisterbau, den der Mensch für sein Verständnis des Weltalls erdacht hat. Man findet darin das Absolute und das Unendliche, das Greifbare und das Unbegreifbare.” (LE CORBUSIER,Architekt, Maler und Bildhauer, 1887-1965)
- “So seltsam es auch klingen mag, die Stärke der Mathematik beruht auf dem Vermeiden jeder unnötigen Annahme und auf ihrer großartigen Einsparung an Denkarbeit.” (ERNST MACH, Physiker und Philosoph, 1838-1916)
- “Das Unendliche! Keine andere Frage hat je den menschlichen Geist so tief bewegt!” (DAVID HILBERT, Mathematiker,1862-1943)
- “Mathematik ist die einzige gute Metaphysik.” (LORD WILLIAM THOMSON KELVIN, Physiker, 1824-1907)
- “Das Geschöpf, das im Inneren einer Muschel lebt, errichtet seinen
- Wohnsitz mit Fugen und Nähten, mit seinem Dachwerk und den verschiedenen anderen Bestandteilen, ganz wie es der Mensch mit seinem Hause tut, das er bewohnt; doch dieses Lebewesen vergrößert Haus und Dach allmählich in dem Maße, in dem sein Körper wächst und sich an die Wände der Muschel anpasst.” LEONARDO DA VINCI, Universalgenie, 1452-1519)
- “Die Mathematik ist das Urbild der Schönheit der Welt.“(JOHANNES KEPLER, Astronom und Mathematiker, 1571-1630)
- “Wer ein mathematisches Buch nicht mit Andacht ergreift und es wie Gottes Wort liest,der versteht es nicht. Jede Linie ist eine Weltachse. Eine Formel ein mathematisches Rezept. Die Zahlen sind Drogen. Die Arithmetik die Pharmazie.” (GEORG PHILIPP FRIEDRICH NOVALIS, Dichter, 1772-1801)
- “Wahrhaftig steckt die Kunst in der Natur, wer sie heraus kann reißen, der hat sie.” (ALBRECHT DÜRER, Maler und Grafiker, 1471-1528)
- “Vielleicht könnte man die Kunst als eine Art von Ordnung ansehen in dem Wirrwarr von Eindrücken, den unsere Seele von der Welt empfängt, als einen Ausdruck menschlichen Lebens und Empfindens dem so ganz ungeheuerlichen Chaos der Natur gegenüber.” (HANS THOMA, Maler, 1839-1924)
- “Ein Mathematiker, der nicht irgendwie ein Dichter ist, wird nie ein vollkommener Mathematiker sein.” (KARL WEIERSTRASS, Mathematiker, 1815-1897)
- “Die Freude am Schauen und Begreifen ist die schönste Gabe der Natur.” (ALBERT EINSTEIN, Physiker,1879-1955)
- “Anschauung ist Offenbarung, ist Einblick in die Werkstatt der Schöpfung. Dort liegt das Geheimnis.” (PAUL KLEE, Maler und Graphiker,1879-1940)”
- Ein Wissenschaftler, der diesen Namen verdient, insbesondere ein Mathematiker, erhält bei seiner Arbeit die gleichen Eindrücke wie ein Künstler; seine Freuden sind ebenso groß und von gleicher Natur.” (HENRI POINCARÉ, Mathematiker, Physiker und Philosoph, 1854-1912)
- “Schönheit lässt sich wahrnehmen, aber nicht erklären.” (ARTHUR CAYLEY, Mathematiker, 1821-1895)
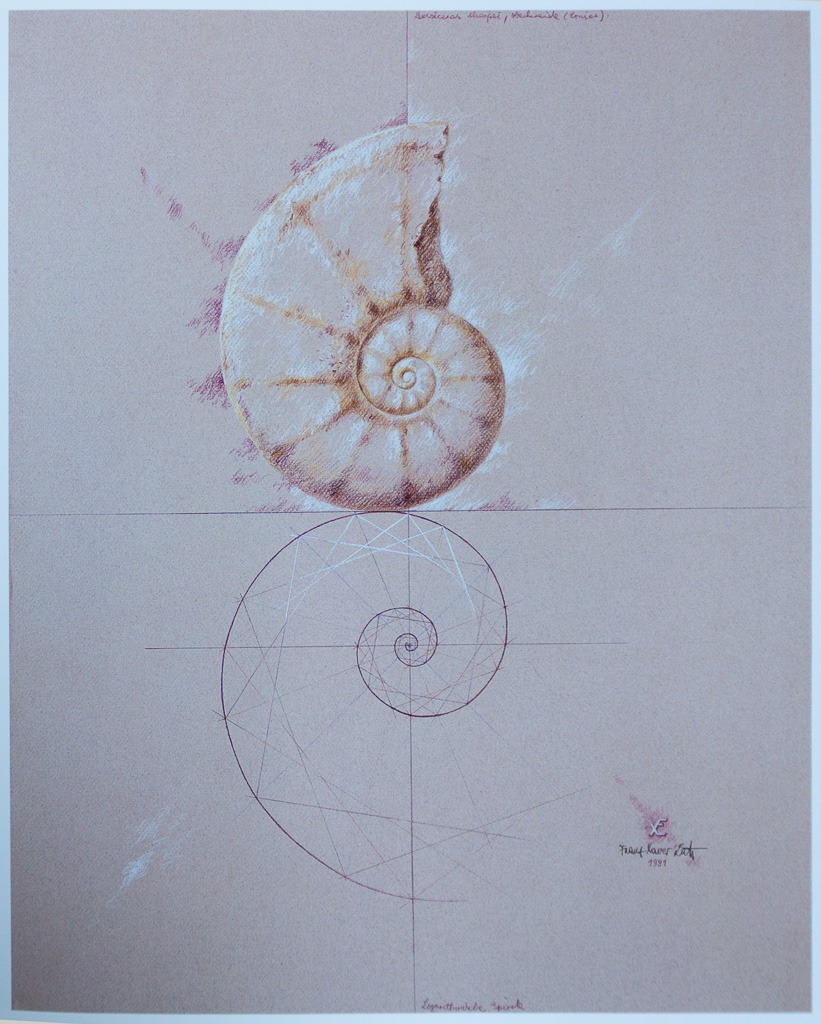
Bei der zum Titelbild gewählten Arbeit “Überprüfung – ohne TÜV”, “Ammonit/Spirale”, 1991, Buntstift auf getöntem Papier, 630mm x 490mm, handelt es sich um ein Thema, das Lutz mehrfach bearbeitet hat. Von dem versteinerten Ammoniten war er so fasziniert, dass der Gedanke nahe lag, über die Konstruktion der logarithmischen Spirale, die Kurve des Ammoniten nachzuprüfen. Diese Überprüfung fand in dieser Arbeit, die zum Titelbild ausgewählt wurde, ihren Niederschlag. Sie zeigt die harmonische Übereinstimmung mit dem gewaltigen Ammoniten.
Auch das nächste Foto zeigt ein Bild zu einem Thema, das der Künstler-Ingenieur mehr als einmal gestaltet hat: “Hyperbelfische”.
Im Katalogtext äußert sich Lutz zu dieser Arbeit und die zwei Wahrnehmungsebenen, die auf eine Ebene projiziert wurden:
Auch beim nächsten Bild “Fichtenzapfen und Parabelkonstruktion”, Acryl auf Leinwand, 1993 kommen sich der Künstler und der Ingenieur besonders nahe. Der Mathematiker ist fasziniert von der Parabel und deren durch Rotation erzeugte räumliche Gestalt, die im Fichtenzapfen sichtbar wird, der Künstler sieht in nächtlichem Licht durch Parabeln geformte schwungvolle moderne Gebäudefassaden. Aus dem glühenden fernen Planeten, der vom tiefen Rot bis zum hellen Gelb leuchtet, scheint sich nach exakt mathematischen Gesetzen die kubische Parabel zu entwickeln.
Faszinierend ist auch das nächste Beispiel: “Der Anfang des Lebens”, Blei- und Buntstift auf Millimeterpapier, 2001. So fesselt uns zunächst die Vielfalt der Eiformen, die die Evolution für die Entstehung des Lebens allein in der Vogelwelt hervorgebracht hat. Dann aber auch das Auftreten der äußeren Eiform in der Technik, und zwar bei der Nocken im Motorenbau. Hier dominiert die mathematische Konstruktion mit Rechnung, Formel usw. Stellt sich die Frage nach einem möglicherweise bestehenden inneren Zusammenhang von Vogelei und Motorteil.
Ästhetisch ansprechend ist das auch das nächste Bild, auf dem die Apfelhälfte sofort den Betrachter anspricht und mit der Form seiner Schnittfläche natürlich die Mathematik ins Spiel bringt, und zwar als Brücke zur technischen Welt des Wankelmotors.
Es handelt sich um das Bild “Eigentlich müsste WANKEL mit Vornamen Adam heißen”, Acryl auf Leinwand, 1992.
Im Folgenden einen kleinen Einblick in die große Vielfalt der Exponate zum Thema Mathematik und Kunst in der Mathothek:
Die ersten sieben Abbildungen zeigen Reproduktionen von Gemälden aus der Renaissance, der Romantik und der Moderne, bei deren Gestaltung der Goldene Schnitt, aber auch eine Parabel eine Rolle spielen.
Die Bilder 8, 9 und 10 spielen auf die menschlichen Proportionen an, die besonders bei den Skulpturen im antiken Griechenland und der Renaissance ihre Höhepunkte erreichten.
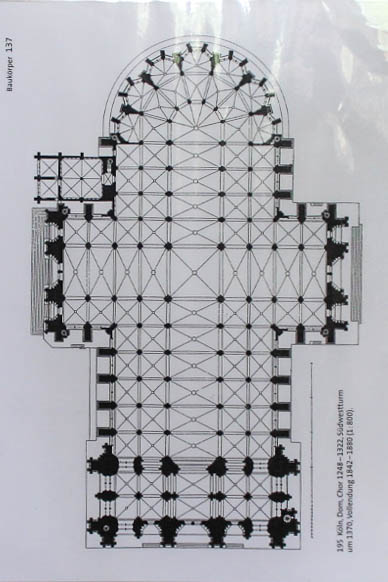
Aber auch im Tempelbau in der Antike und späteren repräsentativen Bauten spielten harmonische Proportionen, wie z.B. der Goldene Schnitt, eine große Rolle. Beispiele dafür sind Objekte der Mathothek, die auf den Abbildungen 10 bis 13 zu sehen sind.
Abbildung 14 zeigt das in der Mathothek vorhandene maßstabsgetreue Modell des Castell del Monte mit seiner tiefen Mathematik.
Die Abbildungen 15 und 16 zeigen minimalistische Arbeiten bedeutender Künstler,17 und 18 sind Beispiele von Arbeiten zum Goldenen Schnitt und zur Goldenen Spirale, die in der Mathothek entstanden sind.
Die Abbildung 19 zeigt ein Beispielset zum Thema der fünf platonischen Körper, die in der Mathothek einen breiten Raum einnehmen, 20 zeigt einen interaktiven Sternkörper.
Auf den Abbildungen 21 und 22 sind das reale Gehäuse eines Ammoniten und der Zusammenhang mit der Goldenen Spirale in künstlerischer Darstellung zu sehen.
Auf zwei interaktive Kunstobjekte, die Arbeiten aus der Konkreten Kunst von Ingrid Hornef nachempfunden sind, verweisen die Abbildungen 23 und 24.
Zum Schluss gibt es nach den “hehren Beispielen” noch ein ermutigendes Beispiel für die Verwendung des Goldenen Schnitts: Dieses kleine und in Zeitnot geschossene Foto zeigt das begehrte Objekt, den Dünsberg bei Gießen ohne den hässlichen Fernsehturm, und zwar genau im Goldenen Schnitt der Horizontlinie. Dieses Ergebnis entstand, ohne dass der “Fotograf” auch nur eine Sekunde an ihn gedacht hat.
Sich mit dem gespannten und vor allem spannenden Verhältnis zwischen der Kunst und der Mathematik auseinanderzusetzen, ist äußerst reizvoll und lohnend. Das schlägt sich auch in der Mathothek und ihren Exponaten nieder. Dass es in der Mathothek überwiegend um die bildnerische Kunst – Malerei und Architektur – und deren Bezüge zur Mathematik geht, hat viele Gründe, vor allem die bessere Chance, geeignete Exponate zu beschaffen. Aber auch in der Musik gibt es sowohl in der alten als auch in vielen modernen Werken sehr oft im Hintergrund viele mathematische Bezüge. Das gilt auch für zahlreiche poetische und prosaischer Werke. Auch wenn der Umfang der Exponate auf diesen Feldern kleiner ist, so gibt es auch für diese Beziehungen der Mathematik zu Musik und Literatur eine ganze Reihe von Beispielen in der Mathothek.