Ohne jeden Hinweis ist die oben gestellte Aufgabe kaum lösbar. Die relative Häufigkeit des Buchstaben Q in dieser vorliegenden kurzen Buchstabenfolge zur relativen Häufigkeit von Q in der deutschen Sprache und die Auffälligkeit des völligen Fehlens des am häufigsten vorkommenden Buchstabens E in dieser vorliegenden Kombination sprechen zunächst einmal für die Vermutung, dass es sich hier um eine Verschlüsselung handeln könnte.
Es gibt (leider: Es gab) in der Mathothek eine Kette mit 260 würfelförmigen Perlen. Jede dieser weißen Würfel zeigt auf vier seiner sechs Seiten ein und denselben schwarzen Großbuchstaben des deutschen Alphabets. Alle 26 Buchstaben kommen vor. Auf dieser Kette findet man unsere Buchstabenfolge, und zwar ab der dritten Perle. Auf den ersten beiden Perlen stehen C und – einmalig auf der ganzen Kette – ein herzförmiges Zeichen (nun bedauerlicherweise nur noch eine schwarze Perle).
Das Herz steht für ein Komma, die 26 Buchstaben für Ziffern. Es handelt sich hier um eine Darstellung der Zahl Pi, natürlich nicht im üblichen 10er-System, unserem vertrauten Dezimalsystem, sondern im 26er-System. Hier fungieren die 26 Buchstaben als die Zeichen für die Grundzahlen 0 bis 25. So wie die Zeichen 0 bis 9 im 10er-System funktionieren. In allen Stellenwertsystemen spielt aber der Stellenwert einer Ziffer die wesentliche Rolle. Im 10er-System bildet die Zahl 10 die Basis. So bedeutet die Zahl 5305, dass sie die Summe aus 5⋅102+3⋅102+0⋅10+5⋅1 ist. In dem hier benutzten 26er-System bedeutet daher CNAB die Zahl C⋅263+N⋅262+A⋅26+B⋅1. Da im 26er-System A=0, B=1, C=2 und N=13 bedeuten, erhalten wir CNAB=2⋅263+13⋅262+0⋅26+1=43.941.
Welche Zahl im 10er-System entspricht nun der Zahl C,DK im 26er-System? Zunächst bedeutet dort C=2, D=3 und K=10 und damit erhalten wir C,DK=2⋅260+3⋅26-1+10⋅26-2=2,130.177.515. Mit mehr Arbeit und Konzentration lässt sich auf dieselbe Weise unser C,CQRPKNKXQSQNCMKGMPSFJTCPF… ins Zehnersystem übersetzen.
Bevor Du das Umgekehrte, die Übersetzung aus dem 10er-System ins 26er-System, versuchst, solltest Du Dich intensiver mit Ziffern und Zahlenschreibweisen auseinandersetzen. Dafür gibt es in der Mathothek viele interessante und interaktive Exponate und auch zusätzlich erklärende Artikel im Katalog der Mathothek.
Vorher solltest Du zur Erholung versuchen, ein brauchbares Wort in der Darstellung von π im 26er-System zu finden. Wenn Du gute Augen hast und eine größere Chance möchtest, ein sinnvolles Wort zu finden, so benutze die gerahmte Karte, die aus dem Mathematikum in Gießen stammt, mit einer wesentlich längeren Darstellung der Zahl Pi in Buchstaben. Du kannst aber auch das Foto (unten) benutzen und dieses auch noch in der Vergrößerung betrachten.
Leider wurde irgendwann die oben abgebildete Kette zerstört. Dabei gingen einige Buchstaben verloren. Somit konnte sie nicht mehr vollständig rekonstruiert werden, d. h. sie ist etwas kürzer als die alte Kette. Diese enthielt anstatt des Komas (jetzt durch eine schwarze Perle ersetzt) ein “Herzchen”. Vielleicht ein Hinweis auf die mentale Verfassung des Täters?
Immerhin ist gegen das Ende der Kette der Aufbewahrungsort der Kette noch lesbar.
Bis heute fragen sich die Mathematiker, ob π eine normale Zahl ist, das heißt, ob sie in einem Stellenwertsystem, z.B. im 26er-System, jede mögliche endliche Zifferngruppe gleichermaßen häufig enthält. So wie es statistisch zu erwarten ist, wenn man die unendlich vielen Ziffern einer Zahl vollkommen zufällig erzeugt. Im Falle, dass π normal in diesem mathematischen Sinne ist, müssten in der unendlichen Buchstabenfolge irgendwann auch die Harry-Potter-Bücher zu finden sein.
Aber bis heute ist die Normalität der Zahl π unbewiesen, ja bislang ist nicht einmal bekannt, ob nicht ab einer bestimmten Stelle nur noch zwei Ziffern auftreten.
Für Besucher, die sich für mehr Stellen hinter dem Komma von π=3,14… interessieren, gibt es in der Mathothek eine gute Möglichkeit dazu mithilfe dieses Bildes, in dem versucht wird, die Unendlichkeit der Anzahl der Nachkommastellen von π durch das “unendlich” kleiner Werden der Ziffern zu vermitteln:
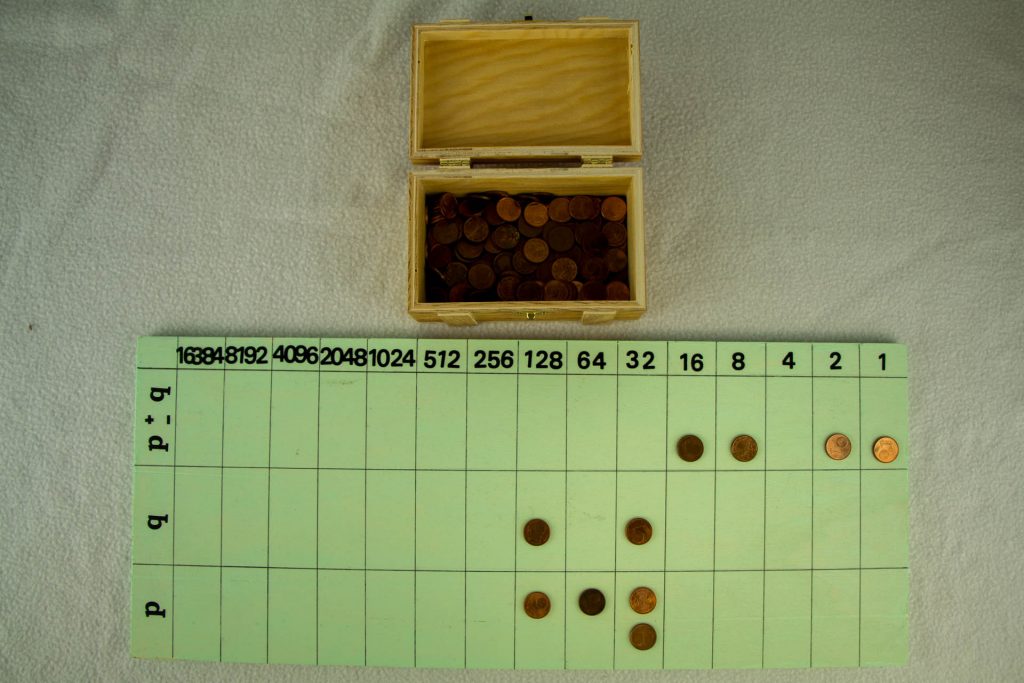
Unten findest Du einige Fotos zu verschiedenen Stellenwertsystemen (5er-, 3er- und 2er-System)