Wie können wir helfen?
Für viele Menschen ist Ordnung machen und halten nicht Top 1 auf der Skala der beliebtesten Tätigkeiten und, wenn doch, macht sich die Umwelt schon ein Mal Gedanken über einen solchen Menschen. Die oft gebrauchte Aussage: “Ich brauche das Chaos, um kreativ zu sein”, ist dann schwer zu widerlegen. Praktisch alle Schöpfungsmythen der Welt beginnen nicht mit dem Nichts, sondern mit dem Chaos – dem Tohuwabohu. Die Erschaffung unserer Welt erfolgt dann durch die ordnende Kraft eines Gottes oder mehrerer Götter. Auf jeden Fall handelt sich den Erzählungen zufolge immer um ein systematisches und Ordnung schaffendes Vorgehen.
In der Mathothek herrscht “natürlich” auch Ordnung und System. Aber die Überfülle der Exponate in dem kleinen Raum und die Begeisterung der Besucher schaffen immer wieder die Voraussetzung für Kreativität und damit das Eingreifen einer ordnenden Hand.
Einige Objekte lassen die Besucher sich interaktiv mit den Tätigkeiten: Sortieren, Ordnen, Suchen und Finden auseinandersetzen.
Zu diesem einfachen Objekt lassen sich beispielsweise die Fragen stellen:
- Welche Farbe kommt am häufigsten vor?
- Wie viele rote, gelbe oder blaue Perlen sind es jeweils?
- Wie viele Perlen sind es insgesamt?
So völlig ungeordnet ist das fast unmöglich, jedenfalls werden die Ergebnisse sehr fehleranfällig sein. Nachdem man die Perlen sortiert und geordnet hat, sind die Antworten schnell und sicher zu finden. So wie in diesem sehr einfachen Beispiel zeigt sich, dass das Sortieren und Ordnen zwar keine Selbstzwecke sind, aber die Grundlage für weiterführende Fragen und Forschungen sein können. Ohne diese Arbeiten mit größeren Datenmengen gäbe es keine Statistik und somit keine begründeten Aussagen über die Wirklichkeit.
Unsere fleißigen Helfer dabei und bei vielen verwandten Aufgaben sind die Computer, die schnell und sicher riesige Datenmengen verarbeiten. Das ist aber nur möglich, wenn der Mensch ihnen Algorithmen zur Verfügung stellt, mit denen sie diese Datenmengen sortieren, ordnen, speichern, suchen und finden können.
Bei dem nächsten Exponat der Mathothek geht es auch um Ordnung, um das Ordnen von neun Zahlen:
Dieses “analoge” Objekt zeigt, dass Ordnung nicht immer auf den ersten Blick erkennbar sein müssen. Es können ganz verschiedene Ordnungsprinzipien gewählt und genutzt werden. Oder kannst Du sagen, welche Reihenfolgen derselben neun Zahlen geordnet sind oder auch nicht? Jeder wird sofort erkennen, dass die Tabelle mit dem blauen Punkt geordnet ist, und zwar nach der Größe der Zahlen. Die übrigen drei Beispiele erscheinen ungeordnet zu sein. Aber das stimmt nicht: Alle Beispiele sind geordnet, nur sind es verschiedene Ordnungen.
In diesem Beispiel wurden für die Auflistung alle Ziffern links von der Hunderterziffer ignoriert, also nur nach der Größe der Zahlen aus den Hundertern, Zehnern und Einen geordnet, d.h. man lässt alle Ziffern bis auf die Hunderter-, Zehner- und Einerziffern weg. Weiß man das Prinzip, ist das Erkennen der Ordnung ein Kinderspiel.
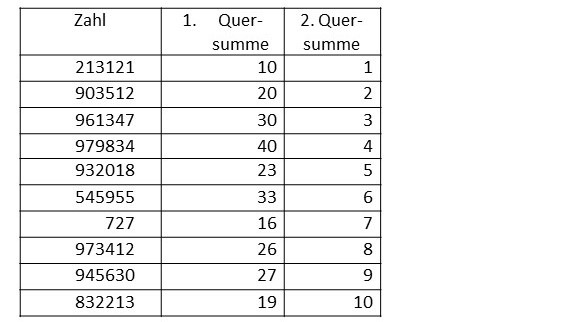
Hier ist es noch schwieriger, die Ordnung zu erkennen. Auch wenn man weiß, dass dieser die Quersummenbildung zugrunde liegt, nutzt das noch wenig. Erst, wenn man von den Ergebnissen noch einmal die Quersummen berechnet hat, erhält man die Ordnungszahl. Hier eine Tabelle mit den Ergebnissen:
Auch im letzten Fall gibt es eine zugrundeliegende Ordnung. Dieses Mal sind die Zahlen nach ihren Resten geordnet, die die Zahlen bei der Division durch 11 liefern.
Diese einfachen und wenigen Beispiele zeigen bereits, dass man Daten nach ganz verschiedenen Kriterien ordnen kann. Dabei kann es sein, dass die Art der Ordnung nicht ohne Weiteres erkennbar sein muss.
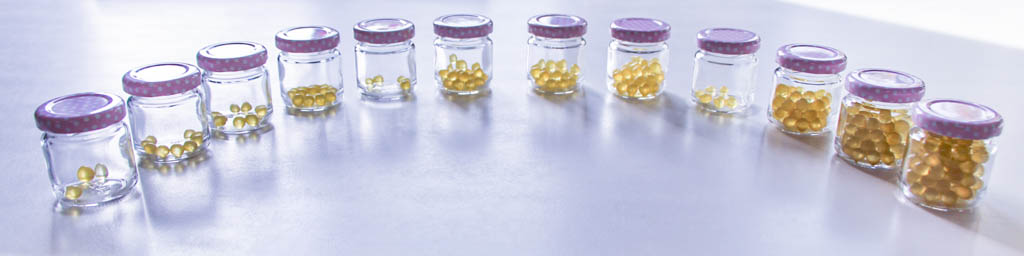
In der nächsten Aufgabe geht es darum, die 12 kleinen Gläser so zu sortieren, dass sie nach ihrer Füllmenge sortiert sind. Dazu suchen wir ein algorithmisches Vorgehen. Das Glas mit den wenigsten Perlen soll am Schluss ganz links in der Reihe stehen.
Um ein Verfahren zu finden, das dann auch in ein Programm für einen Computer übersetzt werden kann, nehmen wir zunächst nur eine Auswahl von fünf Gläsern für eine analoge und schrittweise Sortierung:
Wir stellen die fünf Gläser in eine willkürliche Reihenfolge. Dann vergleichen wir das erste mit dem zweiten Glas, stellen die richtige Reihenfolge fest und machen nichts.
Wir gehen einen Schritt nach rechts, stellen die falsche Reihenfolge fest und tauschen.
Wir gehen wieder einen Schritt nach rechts, stellen die falsche Reihenfolge fest und tauschen.
Wir gehen einen Schritt nach rechts, stellen die falsche Reihenfolge fest und tauschen. Damit haben wir den ersten Durchgang erledigt und das vollste Glas ist ganz nach rechts gewandert.
Wir machen den zweiten Durchgang. Glas eins und zwei stehen in der richtigen Reihenfolge und wir machen nichts. Wir gehen einen Schritt nach rechts, stellen die falsche Reihenfolge fest und tauschen.
Wir gehen wieder einen Schritt nach rechts, vergleichen das dritte mit dem vierten Glas, stellen die falsche Reihenfolge fest und tauschen.
Nach diesem Durchgang sind die beiden Gläser mit den größten Füllmengen ganz nach rechts auf ihre richtigen Plätze gerückt.
Wir machen nun den dritten Durchgang. Vergleichen das erste mit dem zweiten Glas, stellen die falsche Reihenfolge fest und tauschen.
Wir sind fertig. Die fünf Gläser sind nach ihrer Füllmenge geordnet.
Mit diesen Algorithmen lassen sich auch die 12 Gläser nach ihrer Füllmenge ordnen: Von rechts nach links vergleichen wir jedes Glas mit seinem rechten Nachbarn und stellen fest, ob die Reihenfolge stimmt oder nicht. Stimmt die Reihenfolge, machen wir nichts. Stimmt die Reihenfolge nicht, tauschen wir die Gläser. Bis die Gläser endgültig geordnet sind, können mehrere Durchgänge erforderlich sein.
Hier noch einige Bilder von Stationen des Sortiervorgangs der insgesamt zwölf Gläser.
Start: Die 12 Gläser werden zunächst in eine zufällige Reihenfolge gebracht.
Anschließend werden sie mit den oben beschriebenen Schritten in einem ersten Durchgang sortiert. Am Ende des ersten Durchgangs ist das Glas mit den meisten Perlen ganz nach rechts gerückt.
Auf den nächsten Bildern ist jeweils das Ergebnis nach dem 2., 3., 4., 5. und 6. Durchgang abgebildet:
Mit Abschluss des nächsten Durchgangs ( das fünfte Glas wird mit dem sechsten getauscht) ist der Sortiervorgang abgeschlossen:
Diese Art der Sortierung nennt man in der Informatik auch Bubblesort. Es gibt noch etliche andere Verfahren z.B. Election-Sort, die sich in Computersprache übertragen lassen. In der Informatik interessiert bei den verschiedenen Verfahren natürlich besonders, wie viel Zeit diese einzelnen Methoden durchschnittlich benötigen.
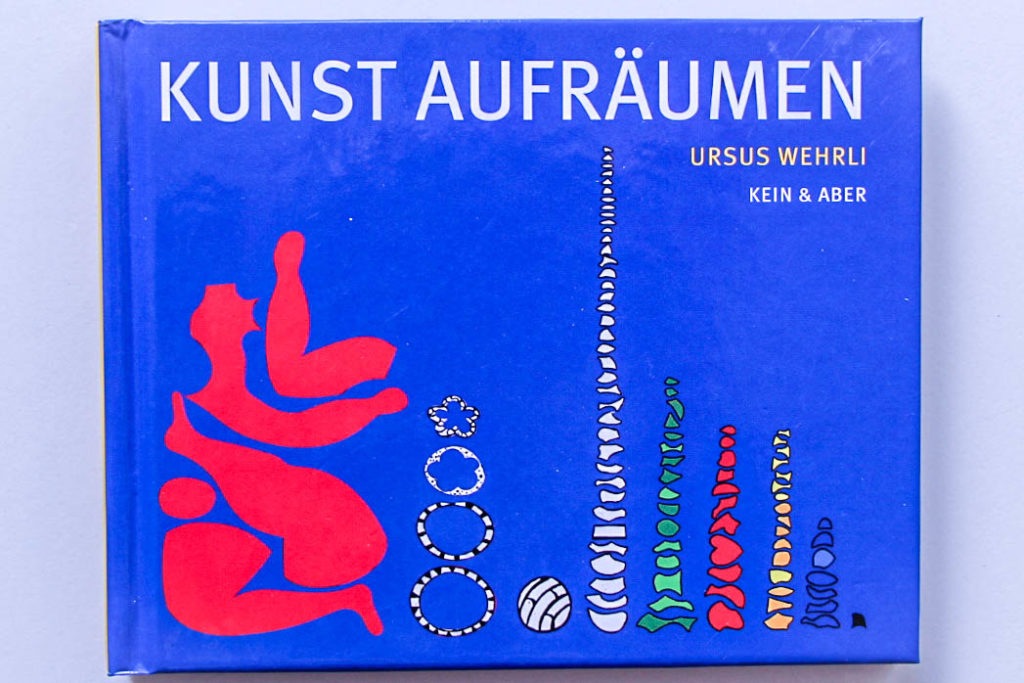
Dass man es mit der Ordnung und dem Aufräumen auch gewaltig übertreiben kann, ist nicht nur eine verbreitete Schülermeinung, das zeigen auch die Arbeiten des Schweizer Künstlers Ursus Wehrli:
Zu diesem Buch gibt es ein schönes Memory-Spiel mit Karten, die paarweise die ungeordneten und geordneten Motive zeigen. Vielen Besuchern der Mathothek macht dieses spielerische “Ordnung-Schaffen” mit den witzigen Motiven von Urusus Wehrli großen Spaß.
Der Künstler Wehrli hat sich als Kunst-Aufräumer auch an die alten Meister gemacht und sich einen Namen gemacht.
Eine wundervolle Argumentation für die Ästhetik und Kreativität einer gesunden Unordnung und gegen die übertriebene tödliche Ordnung ohne Notwendigkeit. Dieser Grundsatz herrscht natürlich auch in der Mathothek, in der die oben abgebildeten Objekte immer wieder Begeisterung auslösen.