Mathothek

In der Mathothek gibt es einige Exponate, die “unmathematisch” verspielt in kleinen szenischen Darstellungen Mathematisches verpacken. “Mit Speck fängt man Mäuse!”

Die erste Szene ist eine schon mindestens seit vielen Jahrzehnten in den Schulpausen und Freistunden immer wieder auftauchende Denksportaufgabe. Hier sind gegenüber der ursprünglichen Formulierung nur der Kohlkopf durch süße Möhrchen und die Ziege durch ein süßes Lamm ersetzt worden

• 

Eine Bäuerin hat ein Boot und möchte einen Wolf, ein junges Lamm und einen Korb mit Möhren. Alle drei möchte sie auf das gegenüberliegende Flussufer transportieren. Leider ist ihr alter Kahn nicht dazu geeignet, sie kann immer nur eines, Wolf, Lamm oder Kohlkopf in ihm mitnehmen. Nimmt sie erst den Wolf. frisst das Lamm die Möhren, nimmt sie zuerst die Möhren, dann macht der Wolf dem Lamm den Garaus. Nur wenn der Wolf mit den Möhren alleine bleibt, besteht keine Gefahr. Sie hat Zeit und findet eine Lösung.

Mit den Figuren der Firma Steiff kannst Du “spielend” selbst nach der Lösung suchen. Oder Du schaust Dir die Bildfolge an und vollziehst die Lösung der Bäuerin nach. Es gibt allerdings noch eine Zweite Lösung.

• 

• 

• 

• 

• 

• 

• 

• 

Wie man in der Folge der acht Bilder erkennt, hat es die Bäuerin in acht Schritten geschafft.  

Es gibt noch eine ähnliche Aufgabe, die sich mit weiteren Steiff-Figuren, die es zu diesem Diorama gibt, darstellen lässt, nämlich die Flussüberquerung der eifersüchtigen Ehepaare:

• 

Zwei Frauen und ihre Ehemänner kommen an einen Fluss. Am Ufer liegt ein Boot befestigt, das höchstens zwei Personen gleichzeitig befördern kann. Da jeder der beiden Ehemänner furchtbar eifersüchtig ist, will keiner seiner Frau erlauben, mit dem anderen Mann allein mit dem Boot den Fluss zu überqueren.

Gibt es trotzdem eine Möglichkeit, wie die vier Personen den Fluss überqueren können?

Ja, auch hier kommen alle heil an das andere Ufer.

• 

• 

• 

• 

• 

• 

Diese Aufgabe stammt aus einem 1612 veröffentlichten Buch des französischen Mathematikers Claude-Gaspar Bachet.

Zu diesem Exponat gibt es in der Mathothek noch weitere Paare, sodass sich die obige Aufgabe erweitern lässt.

• 

Die Graphentheorie ist als Teilgebiet der Mathematik von großer Bedeutung. Unter einem Graphen versteht man im Allgemeinen die zeichnerische Darstellung eines mathematischen Zusammenhangs. Speziell ist ein Graph eine endliche Menge von Punkten und Verbindungslinien, die je zwei Punkte verbinden. Eine Verbindungslinie kann aber auch einen Punkt mit sich selbst verbinden. Die Punkte eines Graphen bezeichnet man als Ecken und die Verbindungslinien als Kanten. Auf die Länge der Kanten und die Größe der Winkel zwischen ihnen kommt es nicht an. Es ist nur wesentlich, welche Ecken mit welchen Kanten verbunden sind. Der ungeheuer fruchtbare Mathematiker Leonhard Euler hat auch die Grundlagen für die Graphentheorie gelegt.

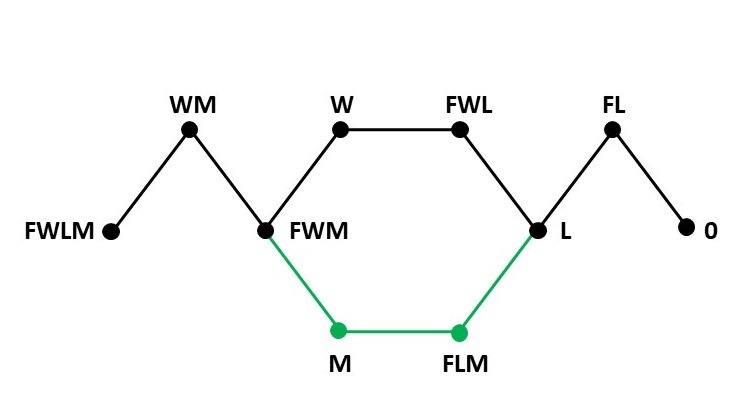
Die Aufgabe, in der die Frau (F) einen Wolf (W), ein Lamm (L) und einen Korb voller Möhren (M) unter speziellen Bedingungen mit ihrem Kahn auf das gegenüberliegende Ufer bringen muss,  lässt sich in dem folgenden Graphen darstellen:

• 

Die zehn Ecken dieses Graphen sind die zehn Situationen, die auf dem Ausgangsufer auftreten können. Zu Beginn befinden sich die Frau, der Wolf, das Lamm und die Möhren (FWLM) an diesem Ufer, dann lässt die Frau  den Wolf mit den Möhren (WM) allein zurück. Jetzt gibt es eine Alternative, sie lässt entweder den Wolf (W) oder die Möhren (M) allein zurück. Im ersten Fall bringt sie das Lamm zurück, d.h. die Frau, der Wolf und das Lamm (FWL) sind am ersten Ufer. Im zweiten Fall bringt sie die Möhren zurück, sodass sich kurz die Frau, das Lamm und die Möhren am alten Ufer befinden (FLM). In beiden Fällen nimmt sie den Wolf ins Boot und lässt das Lamm allein (L) da. Auf der letzten Überquerung befinden sich kurze Zeit die Frau und das Lamm (FL) noch einmal zusammen am alten Ufer. Schließlich nimmt sie dann das Lamm wieder mit, sodass sich keiner mehr (0) am Ausgangsufer befindet. Dieser Weg bzw. diese Lösung ist in den sieben Schritten der Bildfolge dargestellt. Der zweite Weg ist in seiner Abweichung vom ersten im Graphen grün gezeichnet.

Als Übung kannst Du nun versuchen, die Graphen zur friedlichen Überquerung des Flusses von zwei oder drei eifersüchtigen Paaren zu zeichnen.