Wie können wir helfen?
In der Mathothek gibt es ein Modell der Caesar-Scheibe und mehrere ganz verschiedene Exponate zur Verschlüsselungsverfahren aus allen Zeiten. Die Caesar-Scheibe ist eine sehr einfache Methode, um einen Text zu verschlüsseln. Deswegen ist der codierte Text recht leicht zu entschlüsseln. Kennt man die zugrundeliegende Sprache, so hilft z.B. das Wissen über die relative Häufigkeit der Buchstaben in dieser Sprache, natürlich besonders bei langen Texten. Bei der Caesar-Scheibe haben Absender und Empfänger denselben Schlüssel. Der Absender nutzt den äußeren Buchstabenkreis als Klartext und den inneren durch Zuordnung zur Codierung. Der Empfänger macht es umgekehrt, übersetzt den Geheimtext mithilfe des inneren Kreises in den Klartext. Als Schlüssel dient im Beispiel die Zuordnung A↔Q, d.h. das A des Klartextes wurde über den Schlüsselbuchstaben Q gestellt. Damit die Kommunizierenden sich so verständigen können, müssen sie diesen Schlüssel vereinbart haben. Außer A↔A ist jeder andere Buchstabe als Schlüssel geeignet. Damit ist aber auch einsichtig, dass spätestens nach 24 Versuchen, der Code geknackt ist.
Wesentlich sicherer wird die Verschlüsselung, wenn man den Schlüssel häufiger innerhalb einer Botschaft wechselt. Als Schlüssel dient dann eine Buchstabenfolge. “SHZK” beispielsweise würde bedeuten, dass man den ersten Buchstaben mit dem Schlüssel A↔S, den zweiten mit A↔H, den dritten mit A↔Z den vierten mit A↔K codiert. Wenn der Schlüssel länger als der zu verschlüsselnde Text ist, besteht keine Möglichkeit, den Code zu knacken. Um diese Verschlüsselung zu nutzen, gibt es in der Mathothek die Vigenere-Tabelle mit zwei Eingängen: einen für den Buchstaben zur Verschlüsselung und einen für den zu verschlüsselnden Buchstaben. Alle diese auf der Caesar-Scheibe basierenden Wege haben gemeinsam, dass es zum Ver- und Entschlüsseln nur einen Schlüssel für beide Beteiligten gibt. Das ist aber schon beim Briefverkehr der Post anders. Der Empfänger besitzt nur einen Schlüssel (nämlich den für seinen Briefkasten), mit dem er die erhaltene Botschaft lesen kann. Der Absender benutzt als Schlüssel einen, den tatsächlich jeder kennen kann: die Adresse des Empfängers! Auf dieser Idee baut die Möglichkeit der asymmetrischen Codierung mit öffentlichem und privatem Schlüssel auf.
In der Mathothek gibt es ein interessantes Exponat, mit dem man diese Art der verschlüsselten Kommunikation spielerisch durchführen kann. Ebenso lässt sich dabei auch noch einmal leicht das mit dem öffentlichen und privaten Schlüssel erfahrbar machen. Dieses Exponat besteht aus zwei verschiedenen Tabellen:
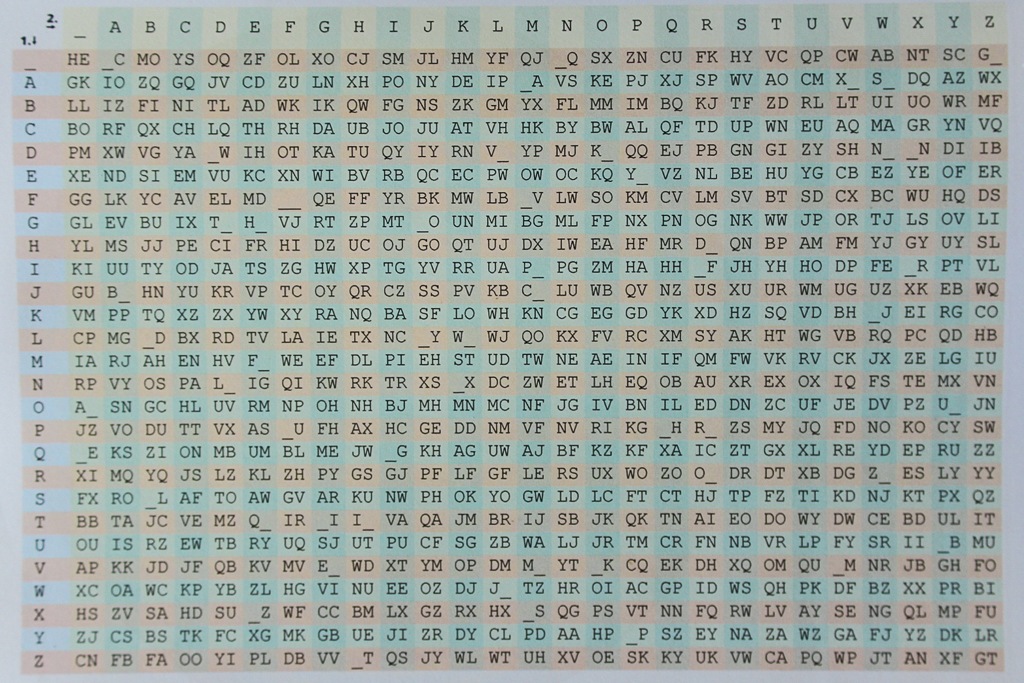
Die linke Tabelle sieht so aus wie das Bild unten zeigt. Diese Verschlüsselungstabelle verschlüsselt die Buchstaben des Alphabets und das Leerzeichen (_). Die zu codierenden Zeichen werden immer mithilfe der beiden Tabelleneingänge paarweise übersetzt. Beispiele: Du→ZY, Karl→PPGE, Heinz_→FRPGCN.
Versucht jemand, weil er irgendwie an den Schlüssel gekommen ist, die Zeichen oben mit demselben Schlüssel zu decodieren, so kommt er nicht an die Botschaft. Schlüssel und Gegenschlüssel sind bei einem asymmetrischen Verschlüsselungsverfahren immer verschieden. In unserem Beispiel erhalten wir, wenn wir es doch versuchen, aus ZY die Buchstaben XF, aus PPGE bekommen wir KGH_, aus FRPGCN ergibt sich LMFHBY. Der Empfänger muss also einen anderen Schlüssel besitzen.
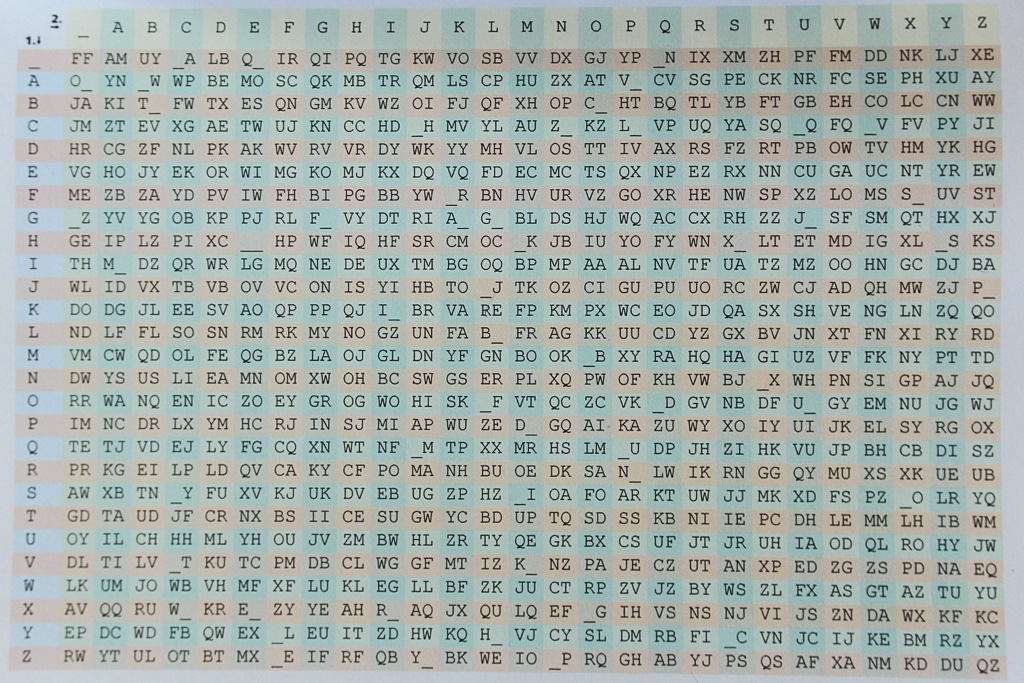
Um die Nachricht zu entschlüsseln, braucht man den unten abgebildeten asymmetrischen Gegenschlüssel. Er ist ebenfalls eine Tabelle mit zwei Eingängen für die Buchstaben des Alphabets und das Freizeichen. Es werden auch hier je zwei Zeichen paarweise verschlüsselt. “Verschlüsselt” man allerdings einen Text, der mit der ersten Tabelle aus der Klarschrift verschlüsselt wurde, so erhalten wir nun als Ergebnis unseren Klartext.
Ein kurzer Test zeigt für unser obiges Beispiel: ZY→DU, PPGE→KARL und FRPGCN→HEINZ_.
Die beiden Tabellen sollen HE-Tabelle und FF-Tabelle (entsprechend der Verschlüsselung von __) genannt werden.
Versuche jetzt, das Wort MATHOTHEK mit der HE-Tabelle zu verschlüsseln und mit der FF-Tabelle das Ergebnis wieder im Klartext zu schreiben.
In einem Rollenspiel kann man nun nachvollziehen, was ein öffentlicher bzw. ein privater Schlüssel ist und wie sich das in der Realität ausnutzen lässt.
Rollenspiel “Publik-Key”:
In einer Gruppe von Besuchern wird nur einer “E” ausgesucht, der alleine die FF-Tabelle als “Privat-Key” in die Hand bekommt, d.h. nur er kennt die Tabelle zur Entschlüsselung. Alle anderen Teilnehmer “A” erhalten die HE-Tabelle als “Publik-Key”, um ihre Nachrichten zu verschlüsseln. Jeder von den Teilnehmern “E” mit dem öffentlichen Schlüssel, kann jetzt an “A” eine verschlüsselte Nachricht schicken, ohne dass ein anderer diese dechiffrieren könnte, falls er sie in die Finger bekäme. Nur der Besitzer “A” ist dazu mit seinem nur ihm bekannten privaten Schlüssel dazu in der Lage.
RJI-ZCFRVMRJI-OWAORRMOOGRBYCSPRJUBOC
Versuche als Kenner des persönlichen Schlüssels die obige Botschaft, die mit dem öffentlichen HE-Schlüssel codiert wurde, in Klartext zu übersetzen. Dazu hast Du hier noch einmal den privaten FF-Schlüssel:
Natürlich kann “E” eine mit seinem privaten Schlüssel verschlüsselte Nachricht senden, die jeder Besitzer des öffentlichen Schlüssels dechiffrieren kann, aber nicht verändern. Dazu benötigte er den privaten Schlüssel von “E”.
Versuche mit dem öffentlichen Schlüssel die unten stehende Nachricht zu entschlüsseln, die von “E” mit ihrem privaten Schlüssel codiert wurde:
_WMCNXYHPRMPVZOECKBG
Dieses Beispiel stammt aus dem schönen Buch Abenteuer Informatik von Jens Gallenbacher. In dem Du eine Menge “Informatik zum Anfassen” und damit auch über asymmetrische Verschlüsselung usw. erfahren kannst.
Das hier gewählte Beispiel ist eine gute Veranschaulichung auch für das Verfahren von öffentlichem und privatem Schlüssel. Tatsächlich sind die heute benutzten asymmetrischen Schlüssel viel schwieriger zu knacken. Man benutzt dazu viel Mathematik und sehr große Primzahlen!
Die Mathothek kann mit vielen interaktiven und anschaulichen Exponaten zum Thema Verschlüsselungsverfahren und anderen Gebieten der Informatik spielerisch experimentierend Erfahrungen zu Algorithmen und typischen Problemen dieses Fachgebiets ermöglichen.