Der geniale schottische Mathematiker John Napier (1550 – 1617), der sich mit Logarithmen und logarithmischem Rechnen beschäftigt hat, fand einen genialen Ansatz für seinen Chessboard Calculator, indem er die Eindeutigkeit der Darstellung der natürlichen Zahlen als Dualzahlen ausnutzte. Als Hardware kann man ein Schachbrett und irgendwelche Chips verwenden. In der Mathothek gibt es ein eigenes 8×8-Brett, gelbe Chips und kleine Messingringe.
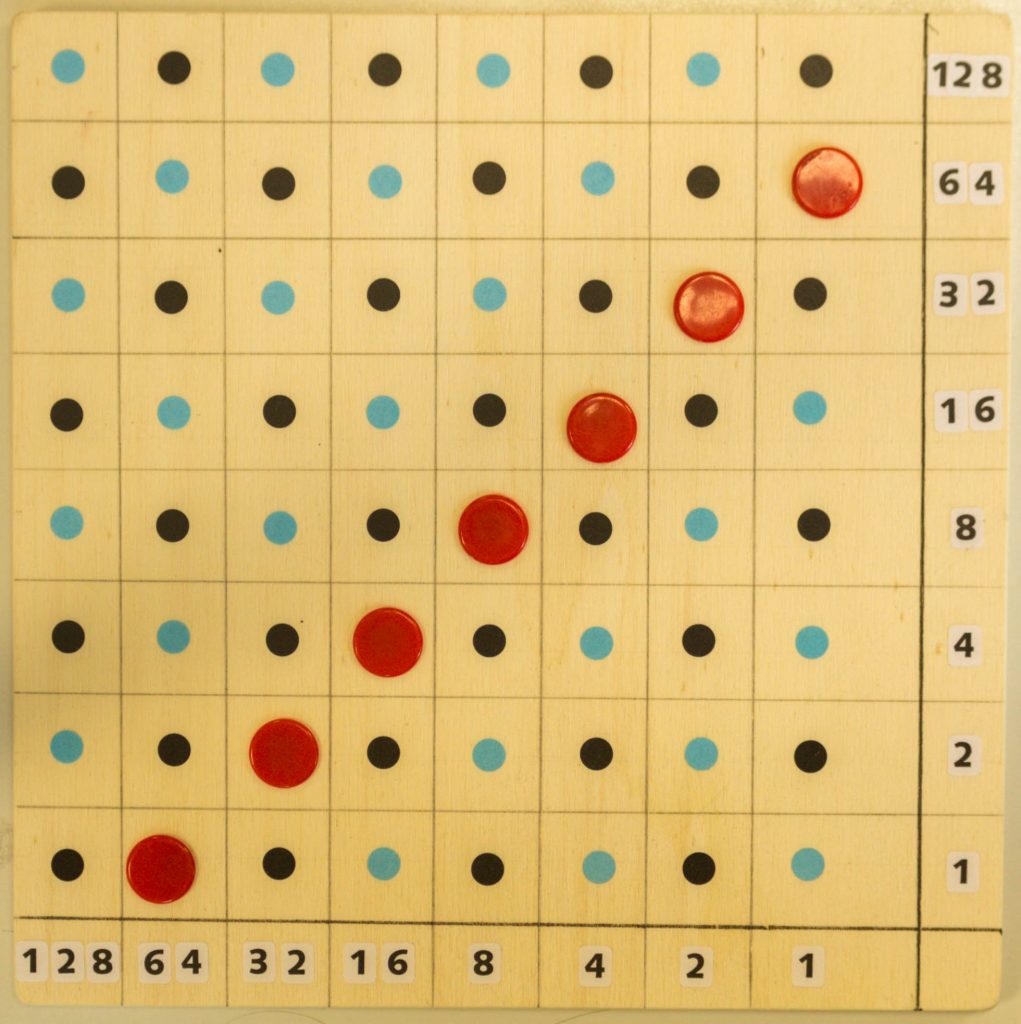
Am Rand unten von rechts nach links und rechts von unten nach oben sind die Zweierpotenzen 20=1, 21=2, 22=4, 23=8, 24=16, 25=32, 26=64 und 27=128 eingetragen. Die blauen und schwarzen Punkte sollen, wie bei einem Schachbrett auch, die Diagonalen besser erkennbar machen. Auf jeder Diagonalen, die von unten links nach oben rechts verläuft sind jeweils alle aus zwei binären Faktoren möglichen gleichen Produkte zu finden. Im folgenden Beispiel sind alle möglichen Kombinationen zweier binärer Faktoren mit roten Chips belegt, die das Produkt 64 ergeben: 1⋅64, 2⋅32, 4⋅16, 8⋅8, 16⋅4, 32⋅2 und 64⋅1.
Als Erstes ein Beispiel ohne weitere Erklärungen. Wir berechnen mit Napier’s Calculator das Produkt 10⋅19=190.
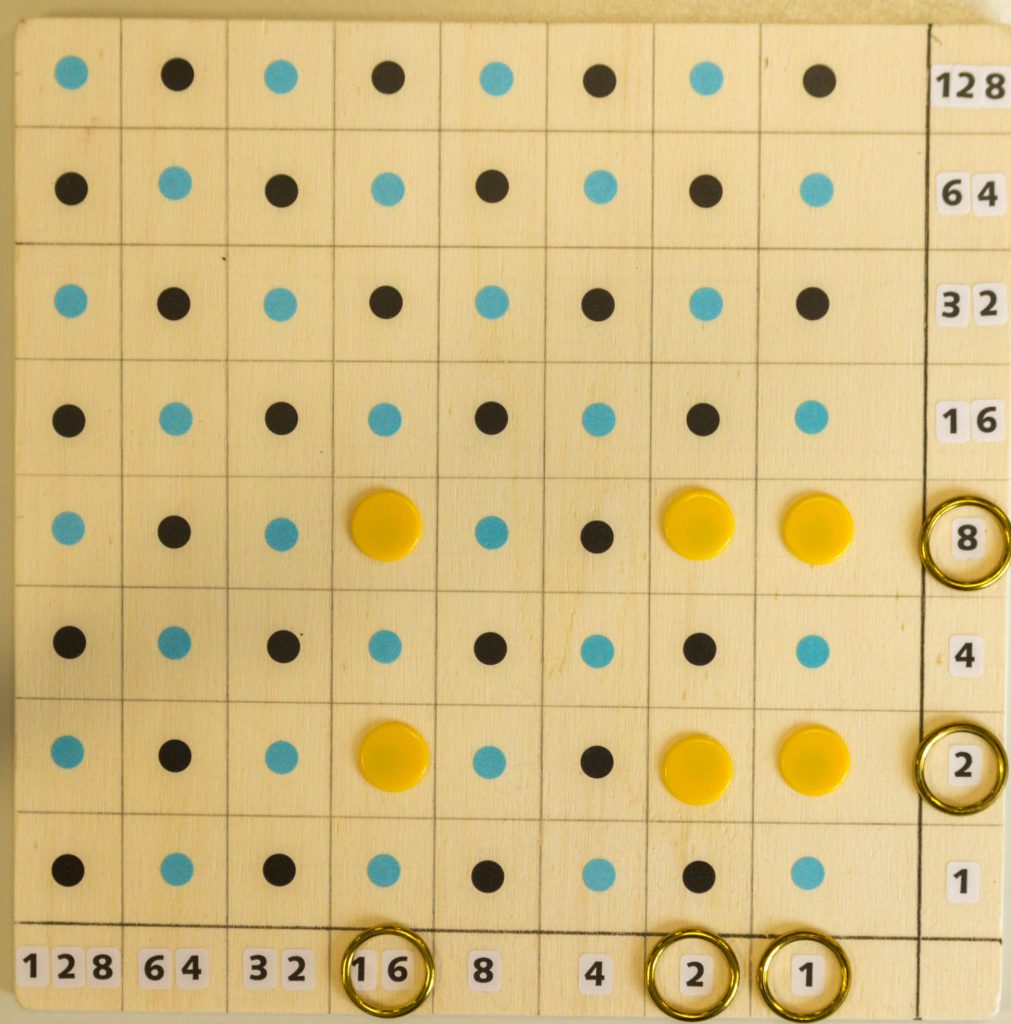
Nun eine zweites Beispiel mit Erklärungen. Es soll das Produkt 22⋅10 berechnet werden. Zunächst zerlegen wir die Zahlen 22 in die Summe der Dualzahlen 16+4+2 und 10 in 8+2. Anschließend markieren wir mit den gelben Chips alle Teilprodukte 2⋅2, 2⋅8, 4⋅2, 4⋅8, 16⋅2 und 16⋅8, deren Summe ist das gesuchte Produkt 22⋅10. Um diese Addition zu erleichtern, verschieben wir alle gelben Chips diagonal nach oben in die letzte rechte Spalte. Die beiden 32er wandeln wir noch in einen 64er um. Die Summe 128+64+16+8+4 ist mit 220 das gewünschte Ergebnis.
Bei dem dritten Beispiel geht es um die Berechnung von 112=11⋅11:
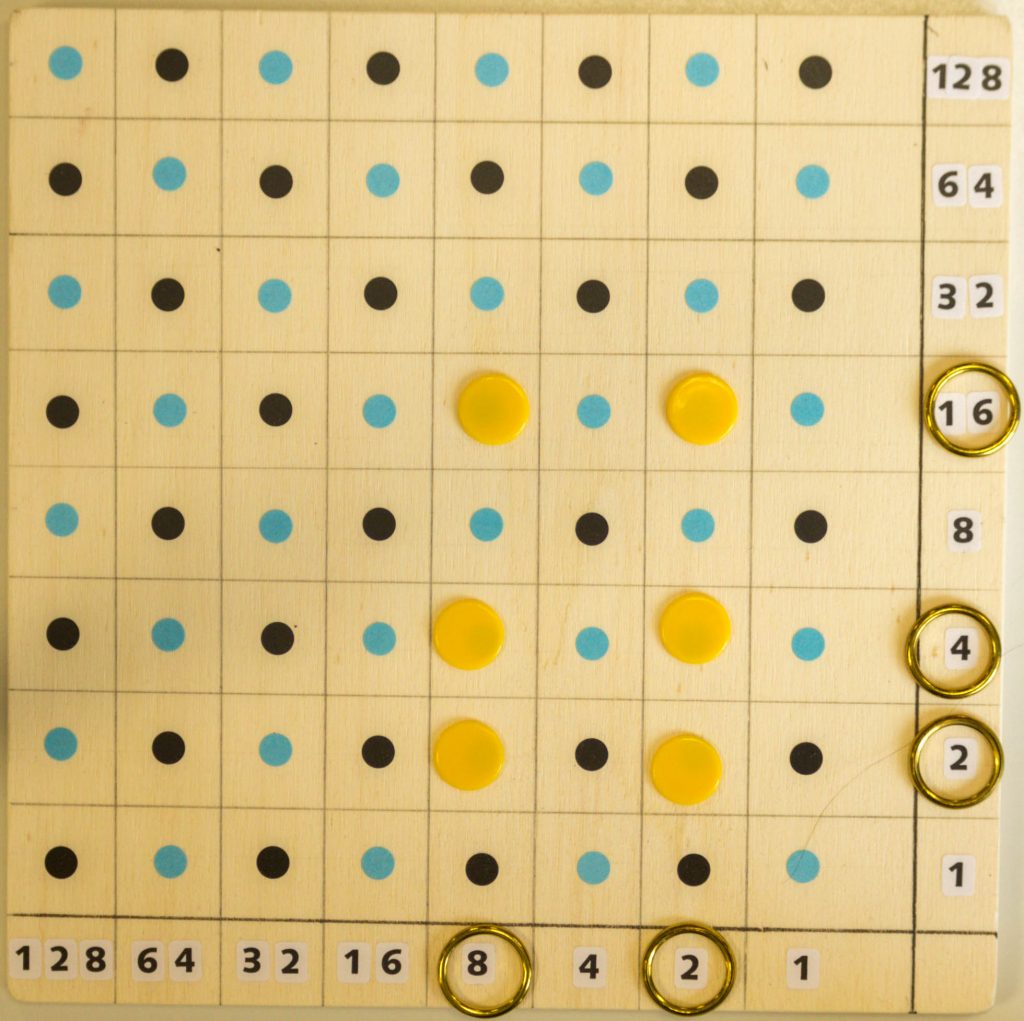
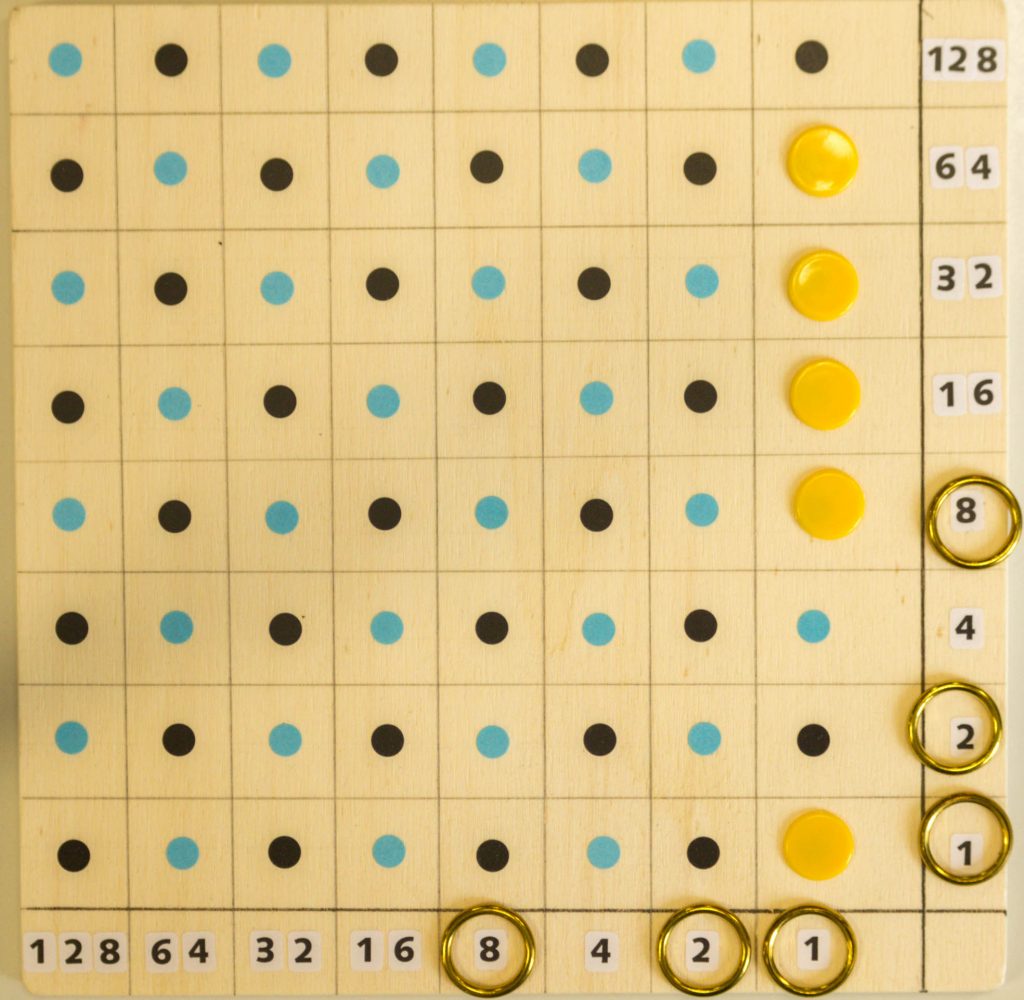
Für die Berechnung von 112=11⋅11 schreiben wir wieder die Zahl 11 als Summe von Dualzahlen, nämlich 8+2+1. Diese Summanden markieren wir jeweils mit einem Messingring auf beiden Achsen. Mit kleinen gelben Chips belegen wir alle notwendigen Produkte 1⋅1, 1⋅2, 1⋅8, 2⋅1, 2⋅2, 2⋅8, 8⋅1, 8⋅2 und 8⋅8. Danach verschieben wir noch die gelben Chips auf ihren Diagonalen nach oben rechts. Damit haben wir alle diese Produkte ausgerechnet und müssen sie nur noch addieren, um das Ergebnis 32+16+8+1=121 der Multiplikation zu erhalten. Dort, wo nach dem Verschieben mehr als ein Chip auf einem Feld der rechten Spalte liegt, müssen wir noch entsprechend dem Binärsystem Ordnung machen, was hier einige Schritte notwendig macht.