Wie können wir helfen?
Im Zusammenhang mit dem Binärsystem gibt es in der Mathothek verschieden lange Teile eines runden Holzstabes, mit denen sich beispielsweise Schüler im Binärsystem messen können. Das ist deswegen möglich, weil die Stäbe bestimmte Längen besitzen.
Die Längen – in cm – der roten und blauen Stäbe sind die Potenzen von 2: 20=1, 21=2, 22=4, 23=8, 24=16, 25=32, 26=64 und 27=128. Das sind die ersten acht Stufenzahlen des Binärsystems. Es sind aber auch die ersten acht Folgenglieder der geometrischen Reihe n→2n für n=0, 1, 2, 3, 4, 5, 6 und 7. Betrachtet man diese Zuordnung x → 2x, wobei man für x jede reelle Zahl einsetzen darf, so erhält man eine Exponentialfunktion. Die entstehende Kurve verbindet dann die ganzzahligen Werte, also die Zweierpotenzen.

Dieses Exponat veranschaulicht ein Beispiel von exponentiellem Wachstum. Von links nach rechts verdoppeln sich die Längen der Stäbe.
Ein Beispiel für exponentielles Abnehmen liefert das Würfelspiel “Blau raus!”

Dieses Spiel kombiniert Wahrscheinlichkeit und potenzielles Abnehmen (negatives exponentielles Wachstum). Zu Beginn würfelt man mit 62 besonderen Holzwürfel, die nur auf zwei ihrer sechs Seiten einen blauen Punkt besitzen. Anschließend legt man die blauen Würfel in das erste Fach. Die zu erwartende Anzahl blauer Würfel beträgt ca. 62⋅1/3, somit verbleiben für die nächste Runde ca. 62⋅2/3 der anfänglichen Würfel. Man wiederholt dieses Vorgehen mit diesen restlichen Würfeln und legt die blauen Würfel in das zweite Fach usw. In dieser zweiten Runde ist zu erwarten, dass ca. 62⋅2/3⋅1/3 blaue Würfel auftreten und ca. 62⋅2/3⋅2/3 Würfel für die dritte Runde zur Verfügung stehen. Dieser Prozess geht so lange weiter, bis kein Würfel mehr zur Verfügung steht. Das Bild oben zeigt zunächst, dass die Stapel Würfel sehr schnell abnehmen. Es fällt auch auf, dass das Stapelende in der Nähe des roten Punktes liegt, der in jedem Fach zu finden ist. Diese Folge roter Punkte entspricht wieder den Gliedern einer geometrischen Folge, nämlich den exakten mathematischen Erwartungswerten. Im ersten Fach ist die Anzahl der blauen Würfel 62⋅1/3, im zweiten Fach sind es 62⋅2/3⋅1/3, im dritten Fach sind es dann 62⋅2/3⋅2/3⋅1/3 usw. Im n-ten Fach liegen also 62⋅1/3⋅(2/3)n-1 blaue Würfel. Durch Vereinfachung erhält man 31⋅2/3⋅(2/3)n-1=31⋅(2/3)n. Diese roten Punkte liegen auf dem Graphen der Exponentialfunktion x→31⋅(2/3)x, wobei x jede reelle Zahl sein kann.
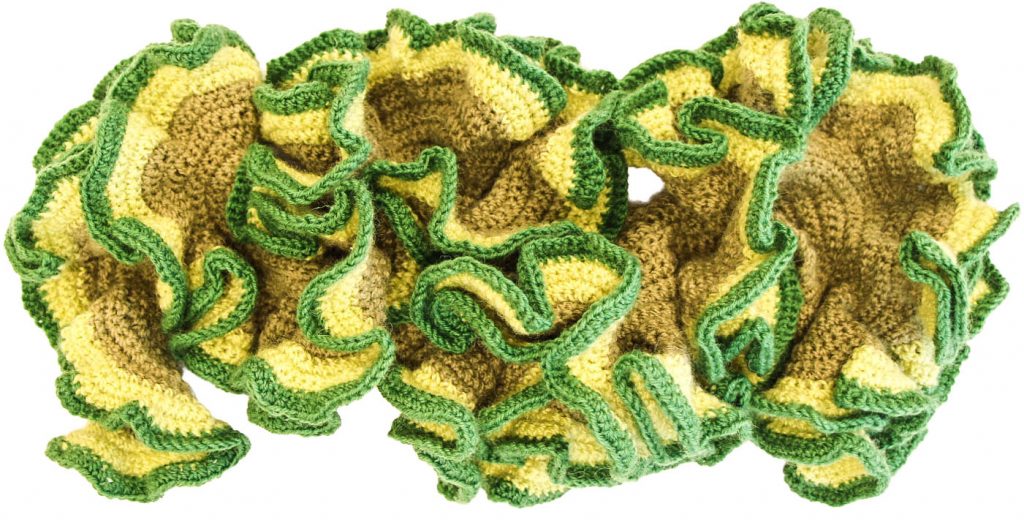
Die nächsten Objekte zum Thema exponentielles Wachstum bestehen aus Häkelgarn und sind “echte Handarbeiten”. Sie erinnern aber auf den ersten Blick auch an untermeerische Korallenbänke.
Alle folgenden Häkelarbeiten begannen mit einer Anzahl von Luftmaschen. Bei jeder weiteren Häkelreihe wurde ein bestimmter gleichbleibender Prozentsatz Maschen zusätzlich aufgenommen. Die überwältigende Zunahme des exponentiellen Wachstums wird bei diesen gehäkelten Objekten “begreifbar” klar.
Im ersten Beispiel wurden mit einem Ring von 15 Luftmaschen begonnen. Auf zwei feste Maschen wurde dann regelmäßig eine Masche neu dazugenommen, also betrug das Wachstum pro Runde ca. 33 %. Eine finnische Mathematikerin hatte diese Idee für die Veranschaulichung einer nicht-euklidischen Ebene, weil Versuche, diese Darstellungen mit Papier herzustellen, misslungen waren. Bei diesem blauen Beispiel ist die Wachstumsrate recht hoch, aber die Anzahl der Runden eher gering, was die Anschaulichkeit einer hyperbolischen Ebene verbessert.
Im zweiten Beispiel waren es anfangs 20 Maschen und es kam nach jeder achten Masche eine neue hinzu, d.h. die Zunahme betrug hier 12.5 % je Reihe
Im dritten Beispiel betrug die Zunahme 20 % in jeder Reihe.
Im letzten Beispiel kam in jeder Reihe nach jeder Masche eine zusätzliche, in jeder neuen Reihe verdoppelte sich also die Anzahl der Maschen, d.h. in jeder Reihe wuchs die Anzahl der Maschen um 100 %. Der Effekt dieses exponentiellen Wachstums führte relativ schnell zum Abbruch der Häkelei.
Wie 0 % Wachstum aussieht, kann man an dem folgenden Teil sehen. Dabei handelt es sich um eine (eigentlich unnötige) Veranschaulichung eines Ausschnitts aus der euklidischen Ebene.
In der Mathothek ist jede Technik gerade recht, um Mathematik begreifbar zu machen. Allerdings ist das Häkeln nicht nur zur Veranschaulichung geeignet, sondern ist auch besondere Technik, die aus einem linearen Faden eine zweidimensionale Fläche schafft, selbst mathematisch durchaus interessant.
Als Beispiel für lineares Wachstum soll ein Exponat der Mathothek gezeigt werden, das zur Veranschaulichung des Hooke’schen Gesetzes dient. Das Objekt besteht aus fünf Stahlfedern und 10 Metallringen, in denen je ein Plastikvogel sitzt. An der ersten Feder hängt kein solcher Ring, an der zweiten Feder hängt ein Ring mit Vogel, an der dritten zwei Ringe mit je einem Vogel, an der vierten sind es drei und an der fünften Feder hängen schließlich vier Ringe mit je einem Vogel.
Der Mathotheksbesucher kann nun erkennen, das jeder weitere Ring die Feder um das gleiche Stück verlängert. Die erste Feder, an der praktisch kein Gewicht hängt, hat die Ausgangslänge. Dann kommt beim ersten Ring durch die Belastung der Feder die typische Zuwachslänge hinzu. Mit jedem weiteren Ring als einwirkende Belastung dehnt sich die Feder ein weiteres Mal um die gleiche Zusatzlänge aus.
Die Folge der Längen ist ein Beispiel für lineares Wachstum: Zu einer Anfangslänge a kommt mit jeder weiteren Belastung eine Zuwachslänge b dazu. Also sehen die Folgeglieder dieser Folge so aus: Das erste Glied ist b, das zweite b+1a. das dritte lautet b+2a und b+3a, b+4a usw. Sie sind die nächsten Glieder dieser arithmetischen Folge: a+n⋅b, wobei n jede natürliche Zahl sein kann. Diese Folgenglieder liegen dann auf der Geraden y=a⋅x+b.
Allgemein beschreibt das Hooke’sche Gesetz die elastische Verformung von Metallen und Festkörpern, wenn deren Verformung proportional zur einwirkenden Belastung ist: z.B. doppelte Belastung ↔ doppelte Verlängerung, zehnfache Belastung ↔ zehnfache Verlängerung, halbe Belastung ↔ halbe Verlängerung usw.
Im Zusammenhang mit Wachstum und Abnahme interessieren sich viele Wissenschaften für mathematische Modelle und Funktionen, um realistische Voraussagen machen zu können. Im Hinblick auf die problematische Umweltentwicklung alarmiert besonders das exponentielle Wachstum. Die Aggressivität dieser Form des Wachstums – in einer Welt mit begrenzten Ressourcen – schafft eine riesige Gefahr für die Umwelt des Menschen.
Eine kleine stachlige Pflanze am Fenster der Mathothek hat eine frappierende Ähnlichkeit zu einer der Häkelarbeiten. Es handelt sich um eine Opuntie, und zwar um eine Opuntia cristata: