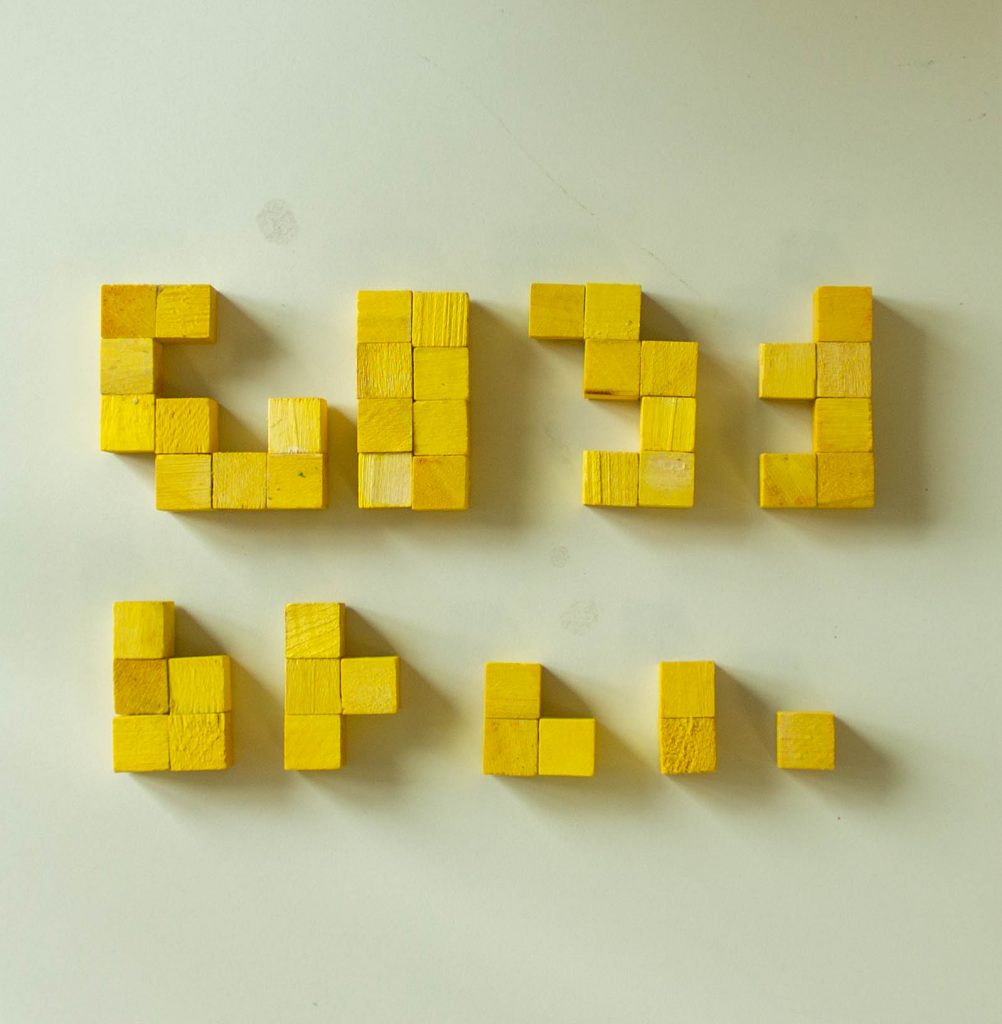Das kleinste magische Quadrat hat die Ordnung 3, d.h. die Zahlen 1, 2, 3, 4, 5, 6, 7, 8, 9 müssen so in ein Schema aus drei Zeilen und drei Spalten angeordnet werden, dass die Summen der drei Zahlen in jeder Reihe, Spalte und jeder der beiden Diagonalen dieselbe Zahl ergeben. In unserem Fall ergibt sich diese magische Konstante aus der Rechnung (1+2+…+9):3=45:3=15.
Bis auf Spiegelungen und Drehungen gibt es nur eine Lösung. In allen Lösungen muss in der Mitte die Fünf stehen. Der Legende nach stieg vor 3000 Jahren in China eine Schildkröte aus einem Fluss. Das magische Quadrat mit den neun Zahlen befand sich auf ihrem Rückenpanzer.
Bei den folgenden vier Varianten der geometrischen Interpretation des kleinsten magischen Quadrates liegt natürlich auch das „Schildkröten-Quadrat“ zugrunde. Allerdings ist die Lösung dadurch erschwert, dass man die Zahlen durch kleine Holzwürfelchen ersetzen muss und die auch noch zu bestimmten Teilfiguren zusammengeklebt sind. Die drei Teile in jeder Zeile, Spalte und Diagonalen müssen zusammen nicht nur immer dieselbe Summe ergeben, sondern durch das richtige Zusammenfügen der drei Teilstücke auch jeweils dieselbe Gesamtfigur bilden.
In der Mathothek gibt es vier Varianten solcher geomagischer Quadrate. Bei den Varianten I und II sind die Teile jeweils zu einem Rechteck aus 3*5 Würfelchen zusammenzusetzen. Bei den Varianten III und IV geht es jeweils um ein 4*4-Quadrat. Da natürlich keine 16 Würfelchen zur Verfügung stehen, sondern nur 15, haben diese beiden letzteren Varianten als Lösung nur ein 4*4-Quadrat mit einem „Loch“. Dieser 16. kleine Würfel fehlt allerdings immer an derselben Stelle des Quadrates. Dazu darf man aber allerdings das Ergebnis drehen und spiegeln.
Variante I
Variante II
Durch Spiegelungen und Drehungen hängen diese mit den weiteren Lösungen zusammen.
Variante IV
Für die Lösung des geomagischen Quadrates ist es bei allen vier Varianten sinnvoll, sich zunächst eine Lösung für die Zahlen 1 bis 9 zu überlegen und dann zu versuchen die drei Teilstücke in jeder Reihe, Spalte und Diagonalen entsprechend der gewünschten Zielfigur zusammenzusetzen.
Hier folgen für jede Variante jeweils eine Lösung:
Übrigens sind die Teile aller vier Varianten naturfarben oder mit natürlichen Farben ( Variante I mit Rote Bete, Variante II mit schwarzem Tee und Variante IV mit Safran) gefärbt.