In allen Fällen handelt es sich um ein 13-Eck, das nicht konvex ist und nach dem von Mathematikern lange gesucht wurde. Es ist aber weder ein Kleidungsstück noch hat es einen Bezug zu dem genialen Physiker Albert Einstein. Es handelt sich hier um eine Kachel oder Fliese, also eine mathematische Form, mit der sich die unendliche Ebene lückenlos und ohne Überlappung bedecken lässt.

Die besondere mathematische Eigenschaft dieser von dem pensionierten Druckanlagentechniker David Smith (USA) 2022 gefundenen Kachel ist es, dass das entstehende Muster nie periodisch wird, egal wie man es zusammensetzt. Diese Vermutung von Smith und die Bestärkung durch den Informatiker Craig Kaplan, der das Potenzial der „Hut-Form“ sofort erkannte, führte dann im Frühjahr 2023 mithilfe weiterer Mathematiker zum Beweis der Vermutung, dass diese Kachel und ihr Spiegelbild tatsächlich zur lückenlosen und nicht überschneidenden Parkettierung der unendlichen Ebene ohne periodische Wiederholung des Musters geeignet ist – im Gegensatz zum Rapport einer Tapete, bei der sich dieser regelmäßig wiederholt.
Hier ist das Bild eines Ausschnitts, der mit „Ein-Stein-Kacheln“ aperiodisch ausgelegten Ebene:

Dass man zu dieser Kachelung nicht nur eine einzige Form benutzen muss, sondern auch ihr Spiegelbild, ließ manche strengeren Mathematiker ein wenig unbefriedigt. Neben den sehr schönen, in der Mathothek hergestellten Shirt-Kacheln mit Holzoptik gibt es inzwischen auch entsprechende mithilfe eines 3D-Druckers hergestellte kleinere Einstein-Kacheln. Hier sind die beiden spiegelbildlichen Formen „in Schwarz und Weiß“ deutlich zu erkennen.

Nur etwa zwei Monate nach der Entwicklung seiner ersten aperiodischen Parkettierung mit nur einer Kachel präsentierte Smith seine „Vampirkachel“. Sie benötigt kein „Spiegel“-Bild, um die Ebene vollständig und aperiodisch zu parkettieren. Allerdings besitzt sie eine Kante mehr. Ihren Namen bekam das 14-Eck, weil ja bekanntlich auch Vampire kein Spiegelbild haben.

Damit war die Suche nach der „Einstein-Kachel“ erfolgreich beendet.
In der Mathothek gibt es auch zwei Mengen von Vampir-Kacheln aus dem D-Drucker, und zwar einmal in einheitlicher gelber Farbe und einmal mit einer gelben und einer grünen Seite:



In gewisser Weise lassen sich aus Smiths erster Entdeckung durch kontinuierliche Verformung weitere, ja unendlich viele weitere „Einstein-Kacheln“ entwickeln. Dazu finden sich in der Mathothek einige Fotos und Hinweise.
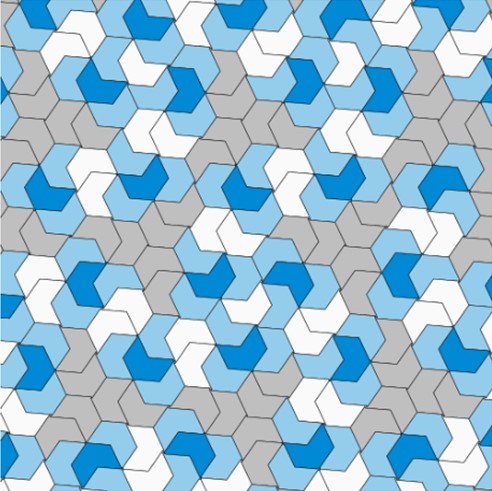
Zu der Parkettierung auf dem oberen Bild gibt es inzwischen in der Mathothek ein weiteres Experiment mit entsprechenden Kacheln aus Sperrholz, die aus v-förmig zusammengesetzten Rauten bestehen. Die Innenwinkel dieser Rauten, Rhomben oder Karos betragen 30° und 60°.

Hält man hier gewisse Legeregeln ein, so lassen sich auch hier aperiodische Kachelungen erzeugen. Das Prinzip des aperiodischen Kachelns wird durch die verwendeten drei Farben gut erkennbar. Andererseits ist die Verwendung der ungefärbten „V-Kacheln“ von großem Reiz im Hinblick auf unsere Fähigkeit, räumliche Strukturen zu erkennen:

Im Falle der V-Kachel ist die Zerlegung in geometrische Teilformen leicht zu erkennen, weil ja jede aus zwei Rauten besteht, deren Gegenwinkel 60° bzw. 30° betragen. Jede Raute wiederum lässt sich wiederum in zwei kongruente gleichseitige Dreiecke zerlegen.

Aber auch die „Shirt-Kachel“ lässt sich aus einfachen geometrischen Formen zusammensetzen:
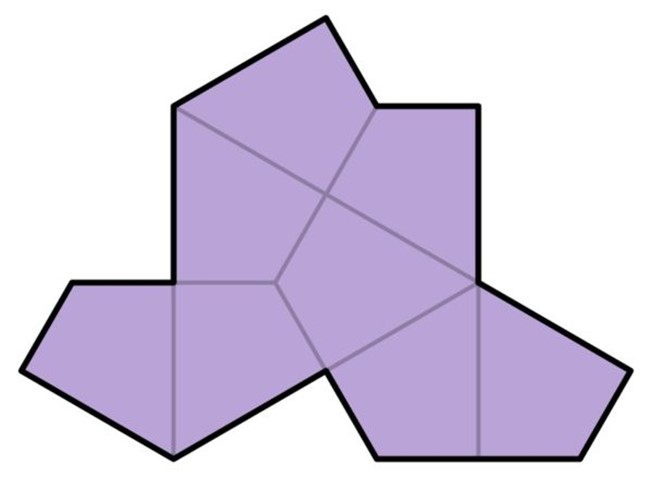

Zunächst kann man die Kachel in kongruente Drachenvierecke zerlegen, die zwei gegenüberliegende Winkel mit 90° und zwei weitere mit 120° bzw. 60° besitzen. Aus diesen Drachenvierecken lassen sich auch gleichseitige Dreiecke und regelmäßige Sechsecke bilden. Teilt man die Drachen entlang der großen Diagonalen, erhält man zwei rechtwinklige Dreiecke, deren zwei weiteren Winkel 60° bzw. 30°. Auch hierzu gibt es entsprechende Legesteine aus Holz für kleine Experimente:



Ein Beweis für die Aperiodizität der „Shirt-Kachelung“ bedient sich nicht direkt der ursprünglichen Ein-Stein-Kachel, sondern vierer verschiedener Cluster, die aus einer Kachel (Dreieck), zwei Kacheln (Viereck und Fünfeck) und vier Kacheln (Sechseck) bestehen. Dazu kommen passende Regeln, wie man diese vier Cluster-Polygone aneinanderlegen darf.
Für die Konstruktion der vier Cluster gibt es in der Mathothek drei Vorlagen:
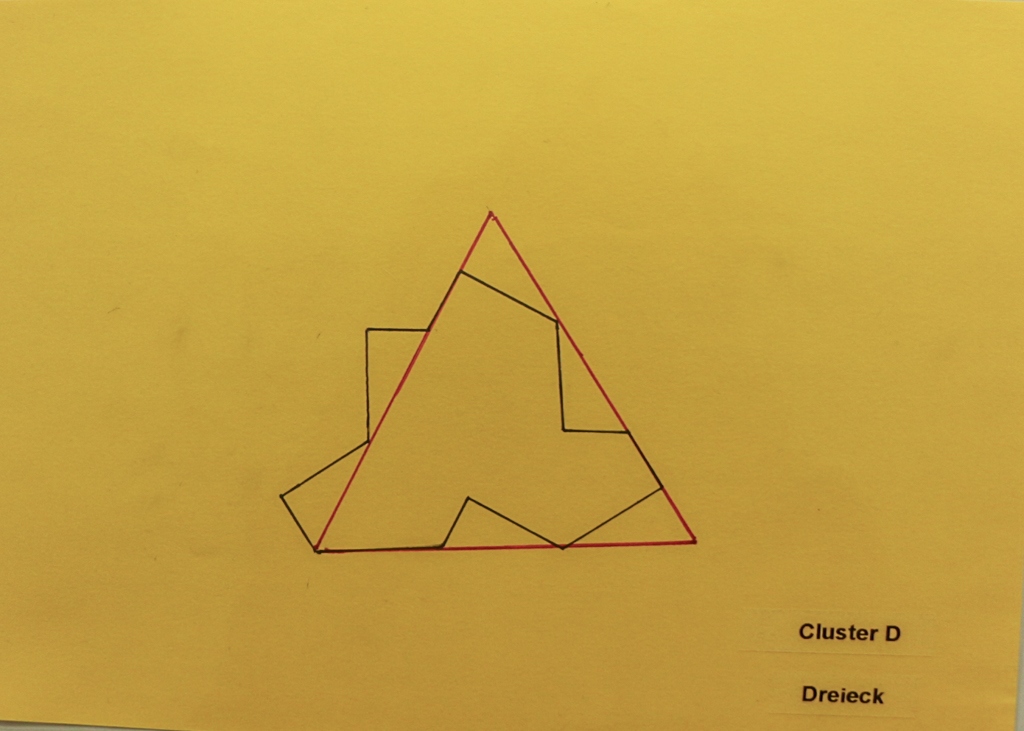
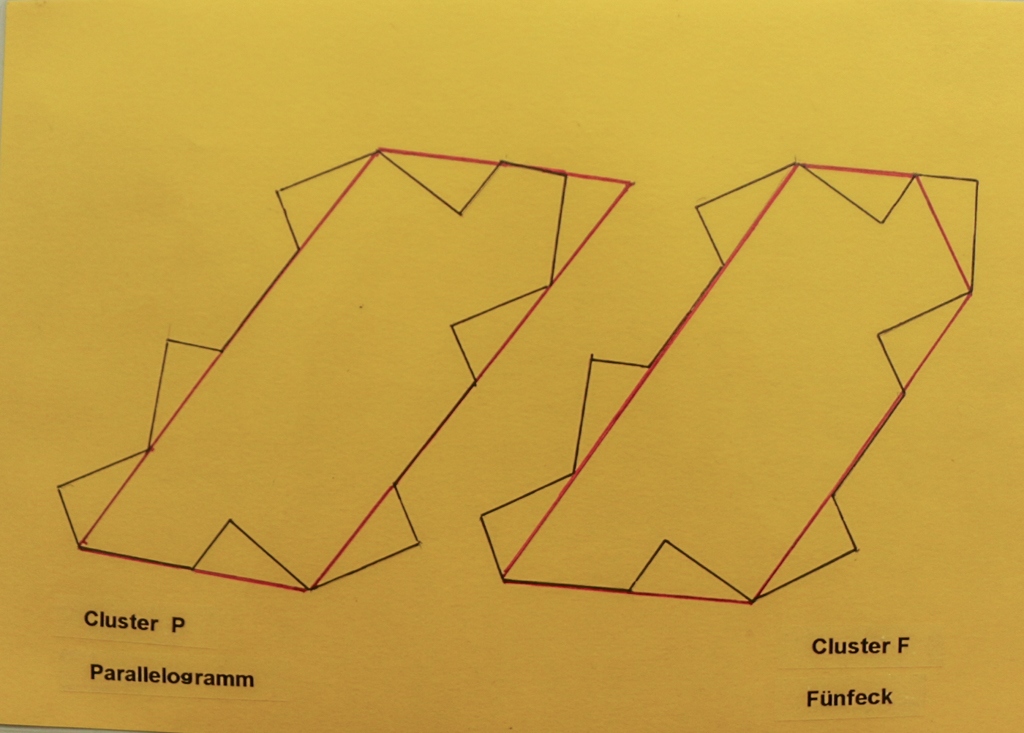

Belegt mit Shirt-Kacheln sehen die Vorlagen dann so aus:



Mithilfe von Kombinationen der vier Cluster entstehen daraus wieder die vier Polygone. Dabei ist diese größere Struktur einzigartig, weil sie nur aus einer einzigen Anordnung der kleineren Cluster-Polygone entstehen kann. Auf der nächsten Stufe kann man die neuen großen Polygone wieder miteinander kombinieren und es entstehen wieder ein Sechseck, ein Fünf-, Vier- oder Dreieck. Auch diese setzen sich aus einer eindeutigen Anordnung der kleineren Polygone zusammen. Das kann man unendlich oft wiederholen und eine hierarchische Struktur erzeugen. Damit und ziemlich viel Computerarbeit konnte dann die Periodizität des erzeugten Musters ausgeschlossen werden. Es gibt aber inzwischen auch einen weiteren Beweis – ohne aufwendigen Computereinsatz.
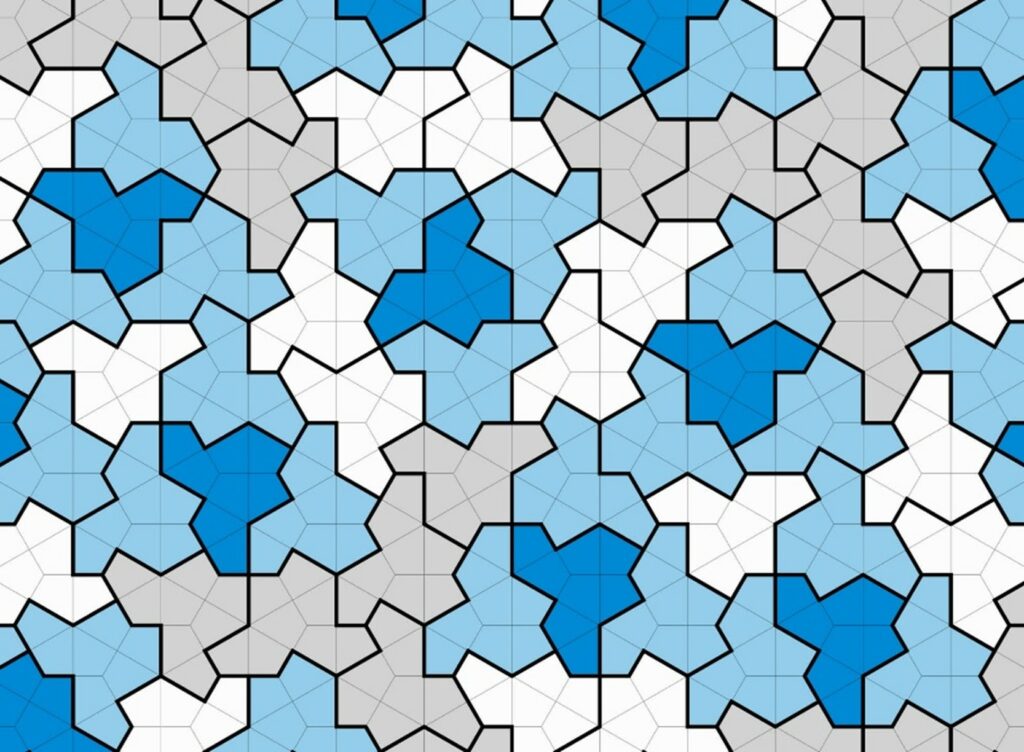
Auf dem folgenden Bild der mit Einstein-Kacheln belegten Ebene ist ein Cluster S mit hell- und dunkelblauer Farbe besonders hervorgehoben:
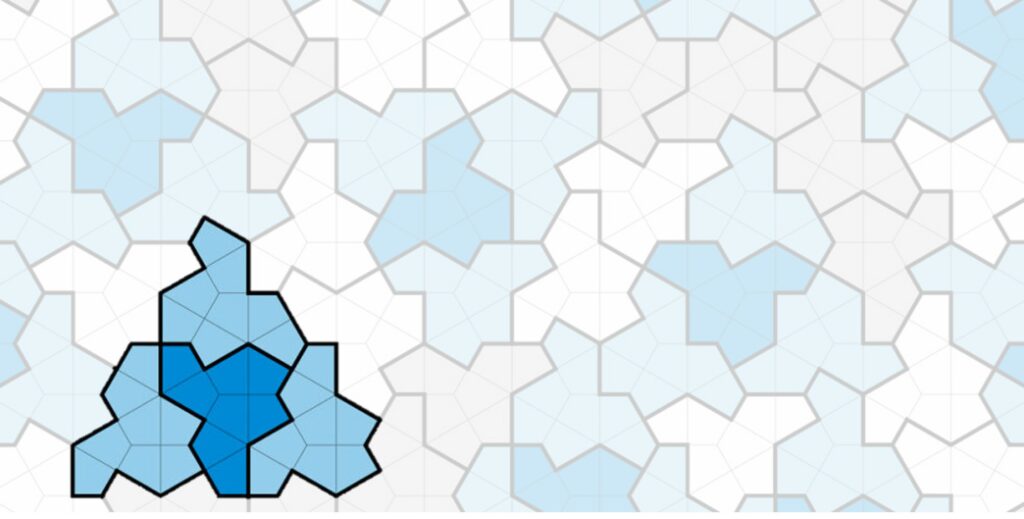
Die nicht-periodische Parkettierung mit der Einstein-Kachel lässt sich gut anhand des folgenden Ausschnitts vermuten:
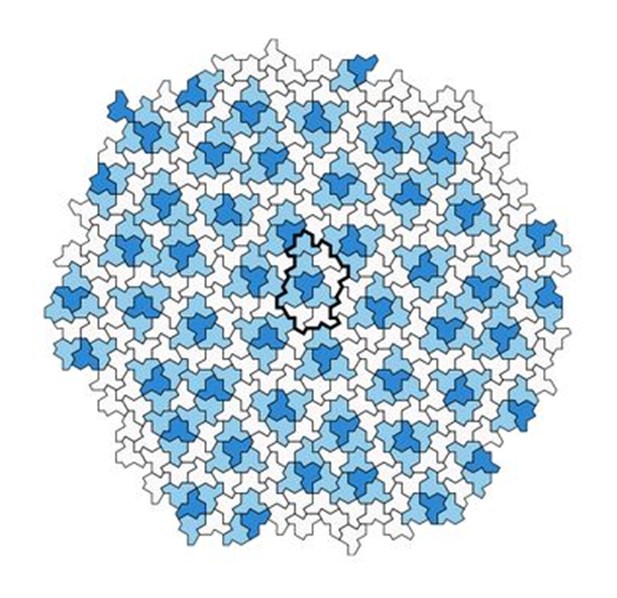
Auch die Cluster P (Parallelogramm) und Cluster F (Fünfeck) sind auf dem folgenden Ausschnitt hervorgehoben:
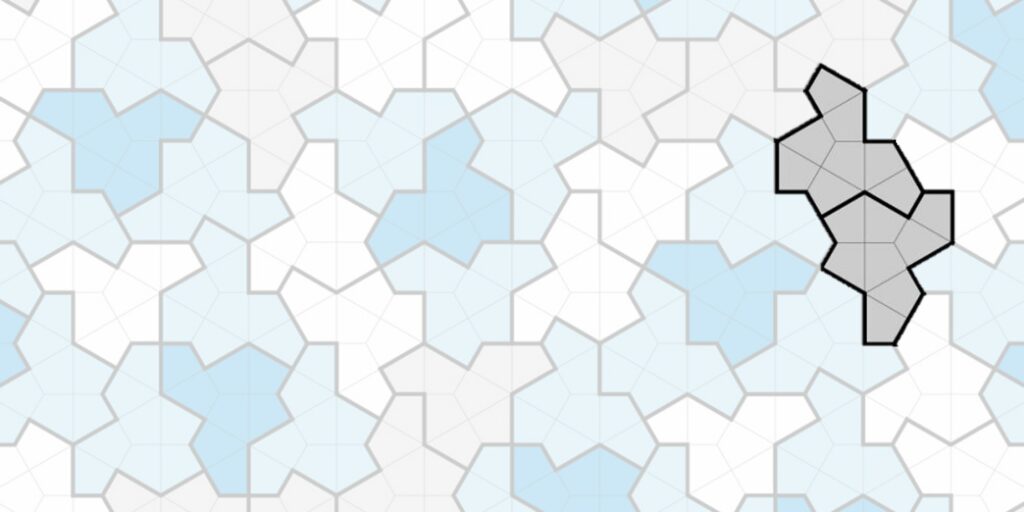
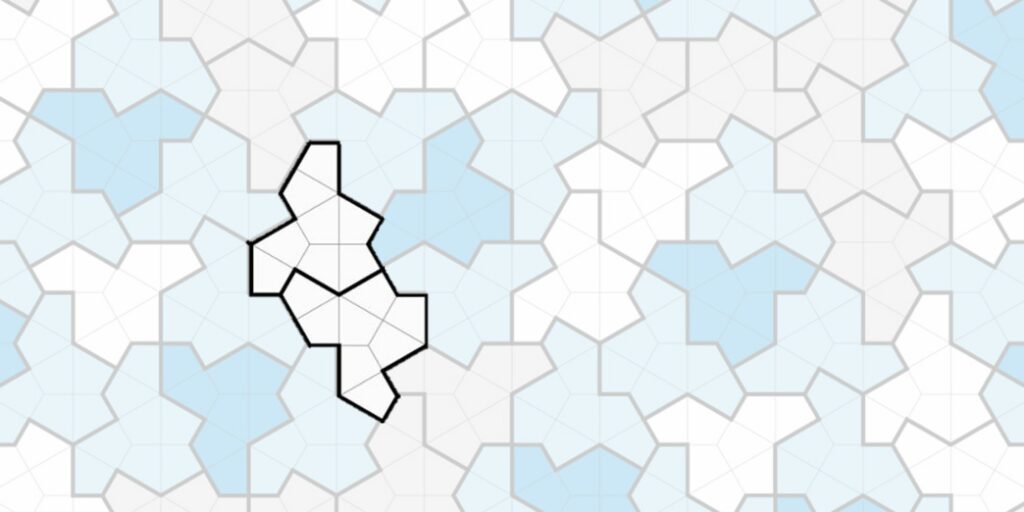
Hier ist nun auch das Cluster D (Dreieck) erkennbar und die Nicht-Periodizität der Einstein-Kachelung zu spüren:
Die „Spectre-Kachel“ ist eine Entwicklung aus der Vampirkachel zu einer mehr organisch anmutenden Einstein-Kachel. Spectre meint in der englischen Sprache „Gespenst“. Diese Kachel ist wie die Vampirkachel dazu geeignet, die gesamte Ebene aperiodisch zu parkettieren, ohne ihr Spiegelbild benutzen zu müssen. Auf dem Boden des Kästchens ist neben einer konkreten Spectre-Kachel (gelb) ein Ausschnitt des aperiodischen Musters zu sehen, das damit parkettiert wurde:

Weniger farbig ist das folgende Bild eines mit „Spectre-Kacheln“ gefüllten Ebenenausschnitts:

Seit es die „Einstein-Kacheln“ in der Mathothek gibt, überrascht immer wieder die Beobachtung, dass gerade das „Einstein-Shirt“ eine ganz große Aufmerksamkeit auf sich zieht. Sobald einige wenige Kacheln aneinandergefügt sind, wächst das Interesse daran, immer weiterzumachen, und auch die Anzahl der Interessenten. Offensichtlich reizt gerade die etwas bizarre Form der Kachel dazu, Merkmale an ihr zu beobachten, die zunehmend Erfolge versprechen.
Symmetrien, Formen und Muster, Strukturen usw. sind durch viele verschiedenartige Exponate und Experimente in der Mathothek sehr stark vertreten. Und sie sind bei jungen und alten Besuchern und Besucherinnen sehr gefragt. So gibt es insgesamt eine sehr große Zahl von „Legespielen“ mit den verschiedensten Bezügen zur Mathematik, aber auch zur Kunst und Natur.
Geometrisch sind da zunächst die sehr regelmäßigen drei platonischen Parkettierungen aus regelmäßigen Dreiecken, Quadraten und Sechsecken:



Dann die zahlreicheren periodischen Parkettierungen mit mehreren regelmäßigen Vielecken, wie die folgenden Beispiele:





Aber auch die aperiodischen Parkettierungen von Penrose mit zwei Kacheltypen sind in der Mathothek vertreten:


Ein paar wenige weitere Beispiele:












