Wie können wir helfen?
Nim-Spiele sind Spiele für zwei Personen, die abwechselnd eine Anzahl von Dingen wegnehmen, beispielsweise Streichhölzer, Münzen oder Spielmarken. Bei den meisten dieser Spiele gewinnt derjenige Spieler, der das letzte Objekt nehmen kann. Dagegen verliert bei der Misère-Variante derjenige, der das letzte Objekt nehmen muss. Natürlich lassen sich diese Spiele entsprechend abwandeln, dass ausgelegte Gegenstände nicht entfernt werden, sondern abgelegt werden: Es werden dann vorgesehene freie Plätze “weggenommen”, indem sie mit entsprechenden Dingen belegt werden. Gewonnen hat dann derjenige, der den letzten freien Platz belegen kann oder – bei der Mísère-Variante – den letzten Platz belegen muss. Diese strategischen Spiele sind von der Spieltheorie bestens erforscht und sichere Gewinnstrategien für den ersten oder zweiten Spieler bekannt. Das besagt, dass derjenige Spieler jedes solche Spiel mit Sicherheit gewinnt, wenn er nach dieser Strategie spielt und keinen Fehler macht. Deswegen wurden diese Spiele schon sehr früh Computern einprogrammiert. Der unaufgeklärte menschliche Spieler hat dann keine Chance mehr zu gewinnen.
Als ein besonders berühmtes Beispiel für ein solches Nim-Spiel ist das Marienbad-Spiel. Es ist eine Variante des Misère-Spiels, die durch den Film Letztes Jahr in Marienbad von Alain Resnais aus dem Jahr 1961 bekannt wurde. Üblicherweise wird dieses Spiel mit 16 Streichhölzern gespielt. In der Mathothek gibt es ein leicht verändertes solches Marienbad-Spiel: Statt Streichhölzer zu entfernen, werden Chips von der roten auf die grüne Seite gedreht. Ansonsten sind die Regeln natürlich dieselben wie beim klassischen Marienbad-Spiel.
Spielregeln:
Die beiden Spieler drehen abwechselnd Chips von der roten Seite auf die grüne, allerdings geht das jeweils nur in einer einzigen Reihe. Dabei kann der Spieler eine beliebige Anzahl Chips umdrehen, mindestens einen, aber auch alle. Wer den letzten roten Chip umdrehen muss, hat das Spiel verloren.
Gewinnstrategie für den nachziehenden Spieler:
Start des Spiels:
Für die Erklärung der sicheren Gewinnstrategie ist die binäre oder duale Schreibweise von Zahlen hilfreich. Daher folgende einfache Verabredung:
1 = (0 0 1)2 ↔ 0 0 1
3 = (0 1 1)2 ↔ 0 1 1
5 = (1 0 1)2 ↔ 1 0 1
7 = (1 1 1)2 ↔ 1 1 1
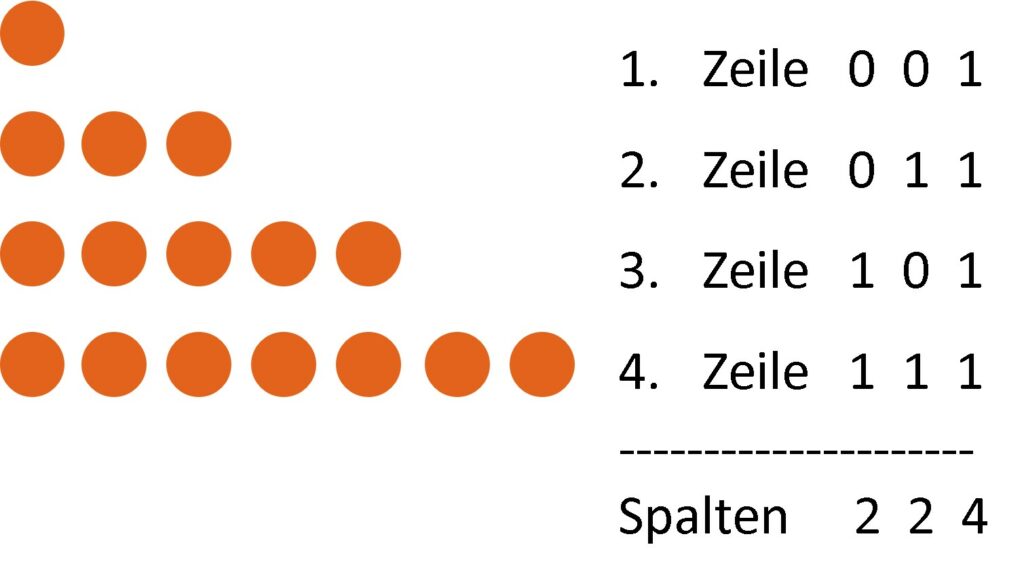
Hier zunächst eine Darstellung der Ausgangsstellung:
Rechts vom Bild des Spielfelds beim Start sind die Anzahl der roten Chips der jeweiligen Reihe in binärer Form angegeben. Unter dem Strich sind Spaltensummen notiert, d.h. in dem obigen Fall ist die erste Spaltensumme 2, ebenso in der zweiten Spalte und 4 ist die Summe aller Einsen in der dritten Spalte, ergibt 2 2 4. Zu Beginn des Spiels sind alle Spaltensummen immer gerade.
Der zweite Spieler muss nun, um das Spiel unbedingt zu gewinnen, folgende zwei Strategien – Anfangs- und Endstrategie – nacheinander beachten:
Anfangsstrategie:
Man lässt den Gegner beginnen. Je nachdem, wie dieser gezogen hat, muss der nachziehende Spieler genau so viele Chips regelgerecht umdrehen, dass danach wieder alle Spaltensummen gerade sind.
Als erster Spieler lässt sich der Sieg nicht erzwingen, ganz gewiss nicht, falls der zweite Spieler die Gewinnstrategie kennt und keinen Fehler macht. Kennt der Gegner die Strategie nicht, muss der erste Spieler auf einen “Fehler” des zweiten hoffen, durch den er bei seinem nächsten Zug so viele Chips entfernen kann, dass danach wieder alle Spaltensummen gerade sind.
Ein Beispiel:
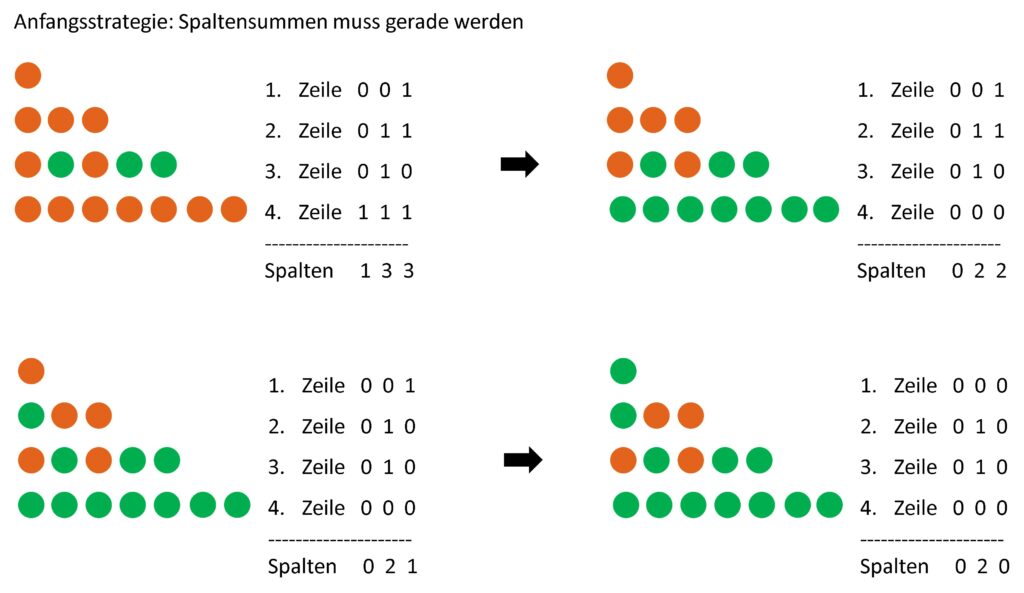
Anfangsstrategie:
Erster Spieler: Zweiter Spieler:
Links in der Darstellung ist der Spielstand nach dem Zug des jeweiligen Spielers und rechts davon die “strategische” Darstellung zu sehen. Dabei ist die Anzahl der roten (noch nicht gedrehten Chips) für jede Zeile als binäre Zahl angegeben. Unter dem Strich stehen die Spaltensummen, d.h. die Anzahl der Einsen in jeder Spalte. Die Strategie des zweiten Spielers besteht nun darin, dass er nun rote Spielsteine so umdreht, dass alle Spaltensummen wieder gerade sind.
Diese Art des Vorgehens setzt der Zweite so lange fort, bis es zu einer Stellung kommt, in der man durch einen Zug nur Reihen mit je einem roten Chip erhalten kann. – Das ist der Augenblick, von dem an man nur noch auf die Anzahl der roten Chips und die Anzahl der Reihen achtet, aber nicht mehr auf die binären Summen.
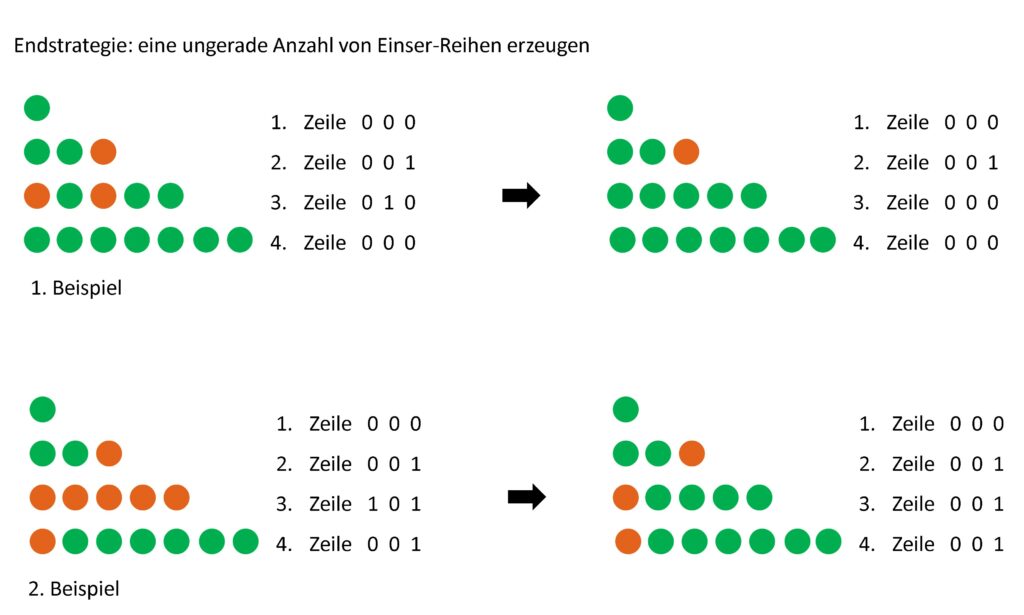
Endstrategie:
Der zweite Spieler zieht nun so, dass sich eine ungerade Zahl von Reihen mit je einem roten Chip ergibt. Dann kann der zweite Spieler erzwingen, dass ersterer den letzten roten Chip umdrehen muss.
Beispiele :
Aus Sicherheitsgründen werden in der Mathothek keine Streichhölzer verwendet, aber es gibt genügend Stäbchen als Ersatz, um das Marienbad-Spiel auch originalgetreu zu spielen.
Interessant in diesem Zusammenhang ist ein weiteres Experiment in der Mathothek: Mit ihm lässt sich elementar nachvollziehen, wie ein “Computer” eine sichere Gewinnstrategie erlernen kann, um in einem Nim-Spiel mit fünf “Streichhölzern” gegen den menschlichen Gegner schließlich immer zu gewinnen.