Tag der offenen Mathothek
Am Samstag, dem 7. März 2020 wird die Mathothek wieder von 11:00 Uhr bis 17:00 Uhr wieder für alle Interessierten geöffnet sein. Eintritt: nur ein wenig Neugierde, Aufgeschlossenheit und Spieltrieb.
Besonderes Angebot: Es besteht dieses Mal die Gelegenheit, einen besonders interessanten Kegelschnitt in seinen Eigenschaften und seinem vielseitigen Auftreten auf sehr anschauliche Weise genauer kennenzulernen. Es geht um die Parabel.
Tatsächlich stehen Euch aber alle über 1000 Exponate zum Anfassen und Experimentieren zur Verfügung. Einen Teil dieser Objekte könnt Ihr schon im Vorfeld kennenlernen, indem Ihr unseren Katalog auf der Website der Mathothek (mathothek.de) besucht.
Mithilfe dieses Exponates kann man zunächst einiges über Kegelschnitte im Allgemeinen erfahren und über die Parabel im Besonderen.
Ein Foto mit sieben Springbrunnen zeigt sieben verschiedene Parabeln aus Wasser. Vielleicht ist dem einen oder anderen bisher noch nicht so aufgefallen, dass es sich hierbei tatsächlich um Mathematik handelt.
Aber dass es auch Parabeln aus Beton gibt, lässt sich oft bei Brücken beobachten. Beim Bau der Heilig-Geist-Kirche in Wiesbaden, ganz in der Nähe unserer Schule, hat der Architekt eine Fülle von Parabelbögen als tragende Elemente seiner Konstruktion eingesetzt. Symbolisch weist die Parabel traditionell aber auch auf das Himmelsgewölbe hin und damit auf die geistliche Seite des Gebäudes.
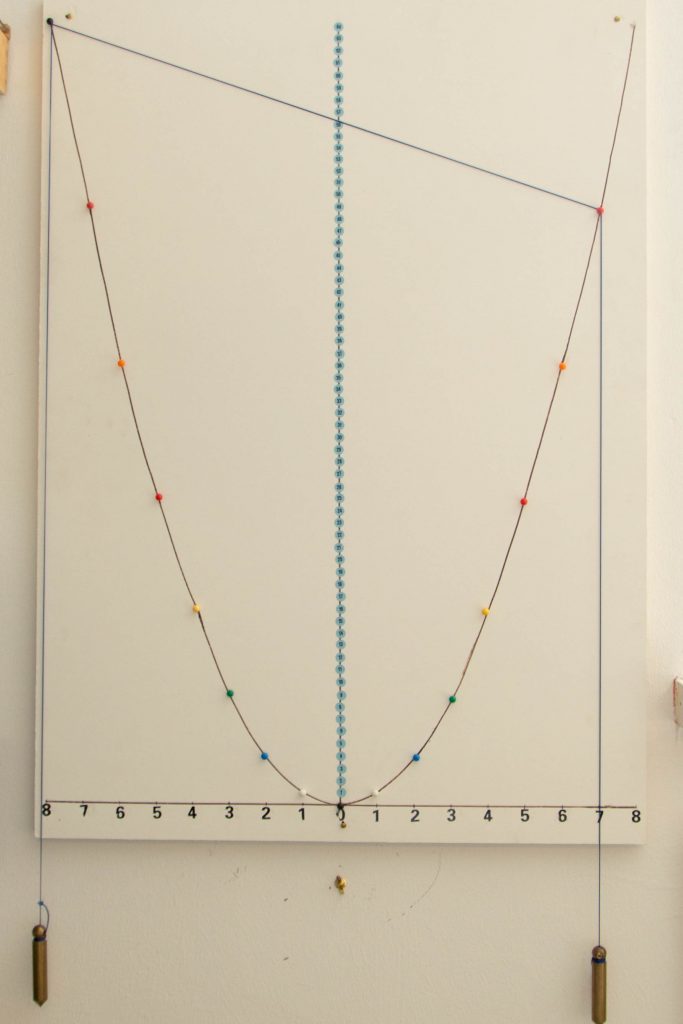
Im Zeitalter von Taschenrechner und Computer ist ein Parabelrechner nicht mehr für das praktische Rechnen von Nutzen, aber mathematisch nicht uninteressant.
Der Konstruktion liegt eine Normalparabel (y=x2) zugrunde. Auf ihr werden die beiden Faktoren markiert. Die senkrechte Achse ist ein Zahlenstrahl mit den nicht-negativen Zahlen. Mit einem beschwerten Faden werden die Faktoren verbunden und das Ergebnis der Multiplikation auf dem Zahlenstrahl abgelesen. Unsere beiden Beispiele zeigen die Rechnungen 8⋅7=56 und 6⋅7=42.
Auch viele Mathematiker wissen nicht, dass die Bezeichnung Parabel aus der Germanistik stammt, ebenso wie Ellipse und Hyperbel. In der Dichtkunst entspricht das erzählte Gleichnis spiegelbildlich der gemeinten Wirklichkeit, ebenso wie der eine Ast der Parabel symmetrisch zum anderen ist.
Eine besondere Herausforderung ist es, das Bild Kreidefelsen auf Rügen mit den Augen eines “romantischen Mathematikers” zu sehen.
2020 – 20 Jahre Mathothek