Es gibt in der Mathematik immer wieder und auf den verschiedensten Ebenen paradoxe Ergebnisse auf oft sehr vernünftige Fragestellungen. Obwohl keinerlei Fehler in der Rechnung und keine logisch falsche Folgerung zu entdecken sind, widerspricht doch das Ergebnis insgesamt unserer Erwartung und Intuition. Die erhaltene Antwort widerspricht anscheinend dem gesunden Menschenverstand.
Eine solche Erfahrung kann jeder Mittelstufenschüler machen, sobald er die Formel zur Berechnung des Kreisumfangs kennengelernt hat:
U=2rπ,
d.h. die Länge des Kreisumfanges ergibt sich aus der Multiplikation des doppelten Radius (= Kreisdurchmesser) mit der Kreiszahl Pi.
In der interessanten Aufgabe wird folgende Frage gestellt: Man stelle sich vor, dass um den Äquator der Erdkugel ein Seil oder eine Kette gelegt wird (ohne Spielraum). Wenn man jetzt diese Kette oder dieses Seil um einen (!) Meter verlängerte und nun diese verlängerte Kette vom Äquator an jeder Stelle gleich weit entfernen würde, reichte dieser Abstand dann aus, damit an jeder Stelle eine Maus über den Äquator und unter der Kette bzw. unter dem Seil hindurch huschen könnte?
Natürlich ist diese Aufgabe nur in der menschlichen Vorstellung möglich und weit entfernt von jeder Realisierung. Aber schnell glaubt man auch über die Antwort sicher zu sein. Einen Meter können wir uns leicht vorstellen, und wir wissen auch noch, dass der Äquator sehr groß ist: etwa 40.000.000 m. Bei diesen Dimensionen scheint eine Verlängerung um den einen Meter so gut wie keine Rolle zu spielen. Die nördliche Maus bleibt also auf der nördlichen, und die südliche Maus bleibt auf der südlichen Halbkugel.
Das folgende Exponat der Mathothek kann uns auf das überraschende und eigentlich nicht zu erwartende Ergebnis vorbereiten.


Die silberfarbige Kette ist 1m lang. Sie wird zur Äquatorlänge in den verschiedenen Modellen hinzugefügt, so wie zum Äquator der „richtigen“ Erde, entsprechend der obigen Aufgabe. Die dunklen Ketten entsprechen den Radien der drei Modellerden.
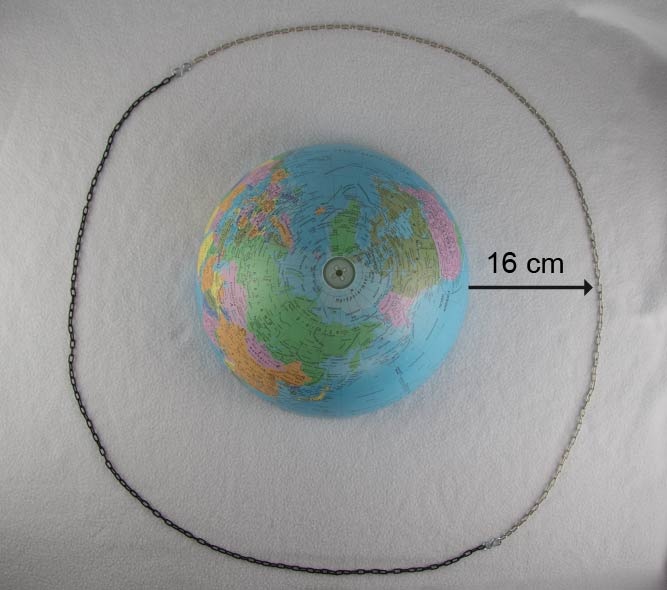
Auf diesen drei Bildern ist jedes der drei Erdmodelle mit seinem um 1m verlängerten Äquator entsprechend der gestellten Aufgabe abgebildet. Achtung: Die vergrößerten Kreise erscheinen nur gleich groß! Aber beim Nachmessen der Abstände erhält bei aller Ungenauigkeit immer ca. 16cm.
Sollte das vielleicht auch bei der realen Erde und ihrem um einen Meter vergrößerten Äquator so sein?
Und jetzt die knallharte Mathematik:
Länge des Erdäquators: π·2R, mit R=Äquatorradius,
Länge des um l verlängerten Seils oder der Kette: π·2R +l,
mit h als Höhe oder Abstand der verlängerten Kette vom Äquator ergibt sich als Länge der Kette π·2(R+h) und damit π·2R+l=π·2(R+h).
Wegen π·2(R+h)=π·2R+π·2h, ergibt sich dann π·2R+π·2h=π·2R+l und daraus erhalten wir π·2h=l und schlussendlich h=l/2π.
Mit 3,14 für π und 100cm für l ergibt sich somit ein Abstand von ca. 16cm. Den Mäusen steht also die Welt offen!
Die obige Argumentation zeigt, dass der Radius R, bzw. seine Länge gar keine Rolle spielt. In jedem Fall bewirkt die Verlängerung um einen Meter denselben Abstand. Das gilt auch in dem Fall, dass der Radius R=0 ist.