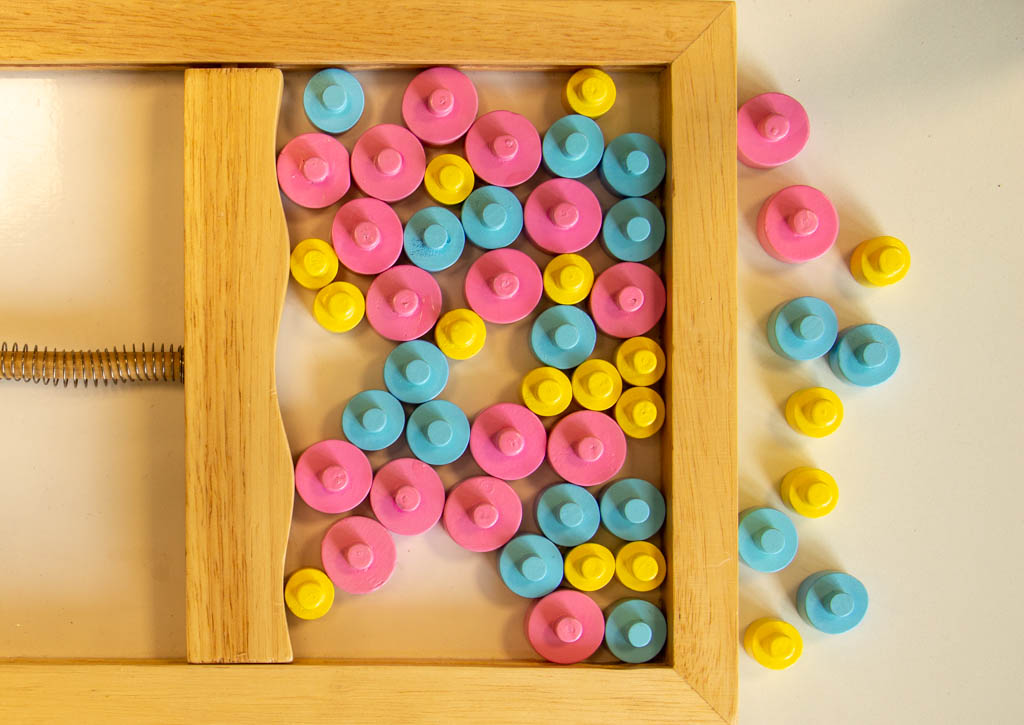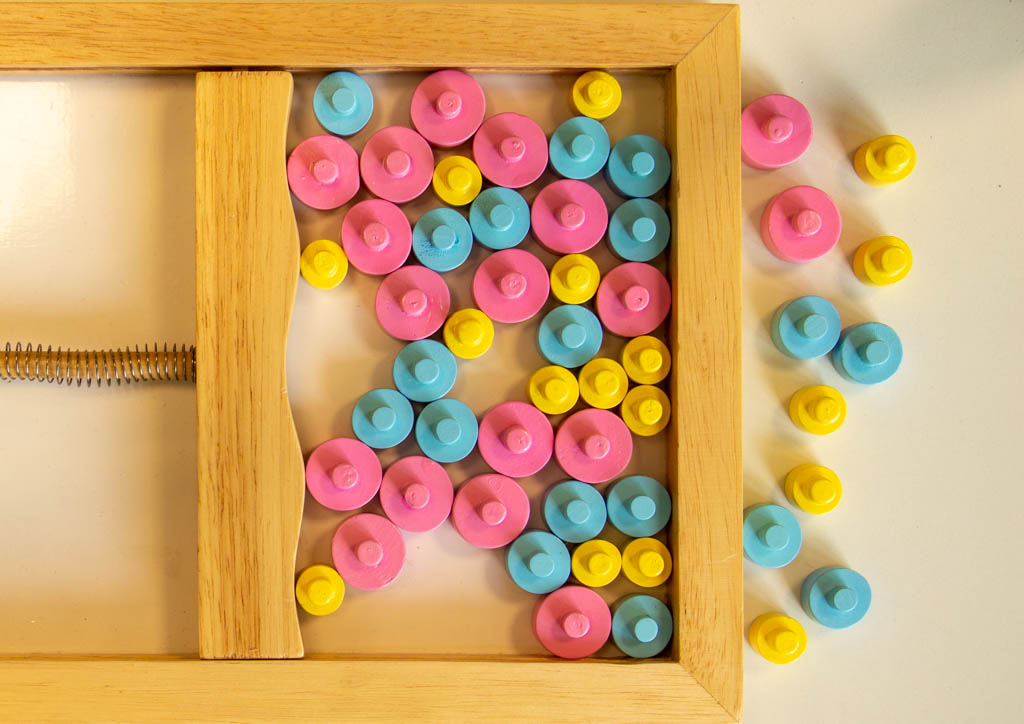Mikado mit Stäbchen ist ein weltweit bekanntes und verbreitetes Geschicklichkeitsspiel. Es besteht meist aus Holzstäbchen, die zufällig auf eine ebenen Fläche zu einem wirren Haufen geworfen werden. Die Spieler versuchen dann reihum, möglichst viele Stäbchen zu entfernen, ohne dass sich der gesamte Stapel bewegt. In diesem Fall kommt der nächste Spieler seine Chance. In der Mathothek gibt es zwar auch Mikadostäbchen, die aber zur Veranschaulichung eines geometrischen und in der Technik geschätzten Körpers, dem einschaligen Hyperboloid, dient.
Ein Scheibenmikado ist ein bei den Besuchern beliebtes und mit dem „Stäbchenmikado“ verwandtes Spiel. Statt der gespitzten und farbig unterschiedlich gestalteten Stäbchen gibt es bei diesem Mikadospiel drei Arten von Scheiben aus Holz, und zwar sind die kleinen Scheiben gelb, die mittleren blau und die großen rosa. Zum Beginn eines Spiels werden alle Scheiben willkürlich zwischen Rahmen und beweglichem Querriegel verteilt. Beim Loslassen dieses Schiebers drückt die Spiralfeder die Scheiben so weit zusammen, bis die Scheiben sich vom Druck der Feder nicht weiter zusammenschieben lassen. Der erste Spieler beginnt mit der Entnahme einer Scheibe. Dabei dürfen sich die anderen Scheiben nicht bewegen, ganz analog zum gewöhnlichen Mikado. Sobald das Gefüge der Scheiben bei dem Entnehmen einer Scheibe sich bewegt, ist der nächste Spieler an der Reihe. Das Spiel endet, wenn alle Scheiben entfernt sind oder nach einer vereinbarten Anzahl Runden. Gewonnen hat, wer die meisten Punkte erzielt hat. Dabei zählt eine gelbe Scheibe einen Punkt, eine blaue zwei und eine rosa Scheibe drei Punkte.
Hier eine Bilderserie mit schrittweiser Entfernung von Scheiben, und zwar bis sich die verbliebenen Scheiben bewegten.
Zunächst wurden die Scheiben vom Druck der Feder mit dem Schieber zusammengeschoben, und zwar bis zu einem stabilen Gefüge:
Ohne Störung der Lage der anderen Scheiben wurden nun Scheiben entfernt, und zwar so lange sich die restlichen Scheiben nicht bewegten:
Das Foto zeigt sehr deutlich, dass nicht jede Scheibe zur Stabilität der Anordnung beiträgt, dass der Druck zur Minimierung des leeren Zwischenraums nur von einem Teil der Scheiben abgefangen wird. Aber beim Entfernen einer bestimmten blauen Scheibe (rechts oben wurde die mittlere der drei blauen Scheiben entfernt) ging es genau um eine solche Scheibe mit Stützfunktion:
Diese Variante des alten Mikadospiels ist bei den Besuchern recht beliebt und hat den Vorteil, dass es hier nicht wie beim klassischen Mikado um die besonders ruhigen Hand- und Fingerbewegungen geht, sondern wesentlich auf das Erkennen, ob die Scheibe eine Stützfunktion im Gesamtgefüge der Scheiben hat oder nicht. Hier ist der Zuwachs an intuitiver Erfahrung schon nach wenigen Spielen erstaunlich.
Auch die Holzperlen, die durch einen Faden zu einer lockeren Kette verbunden wurden, vermitteln eine erstaunliche Erfahrung mit statischer Stabilität: Zuerst bildet man einen hängenden Bogen, dann spannt man den Faden fest an und dreht den Bogen nach oben:
Aus der frei fallenden Kettenlinie entsteht ein optimal stabiler Bogen, weil hier die Kräfte sehr gut – tangential zur Kurve – nach unten abgeleitet werden.
Ohne die zunehmenden Erfahrungen und Erkenntnisse über diese Kraftlinien, die Wirkung von Zug- und Druckkräften hätte es keine stabilen Bögen, Gewölbe oder Brücken gegeben. Die himmelwärts strebenden Kirchen des Mittelalters wären ohne die Erfahrung und das Wissen über Ableitmöglichkeiten dieser Kräfte nicht geschaffen worden.
Die drei ersten Bilder zeigen den Dom von Limburg (spätromanisch, frühgotisch), den Kölner Dom (hochgotisch) und die Heiliggeistkirche in Wiesbaden (modern), mit ihrer Anwendung der Parabel, bzw. Kettenlinie):
In der Mathothek gibt es noch mehrere Experimente zu diesem Thema. So zum Beispiel verschiedene Brücken
und Anordnungen von Kreisen und Kugeln: