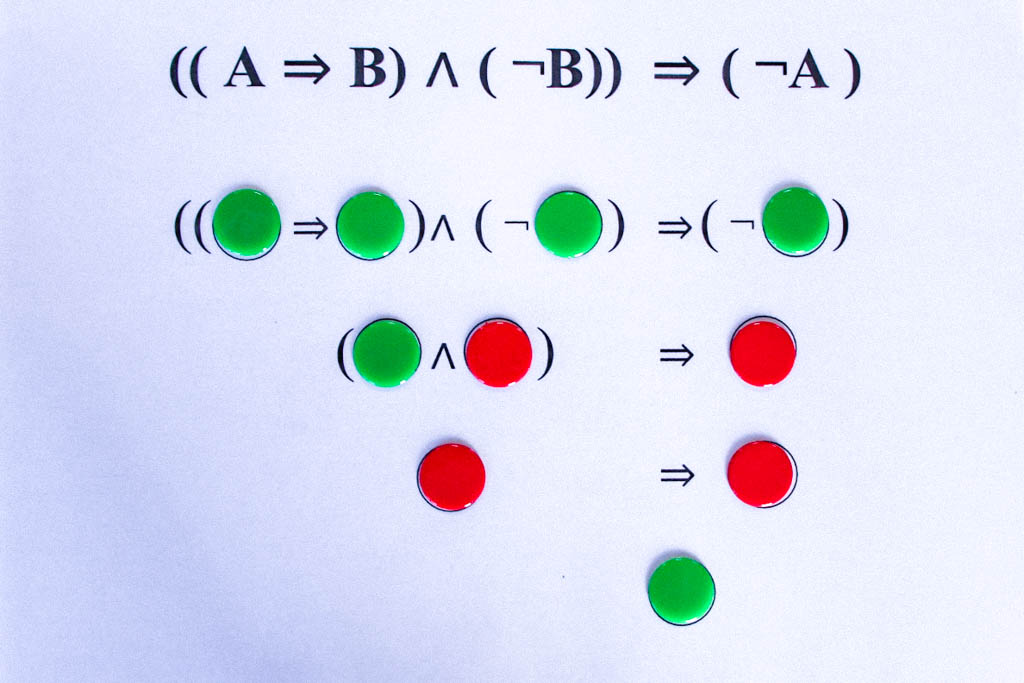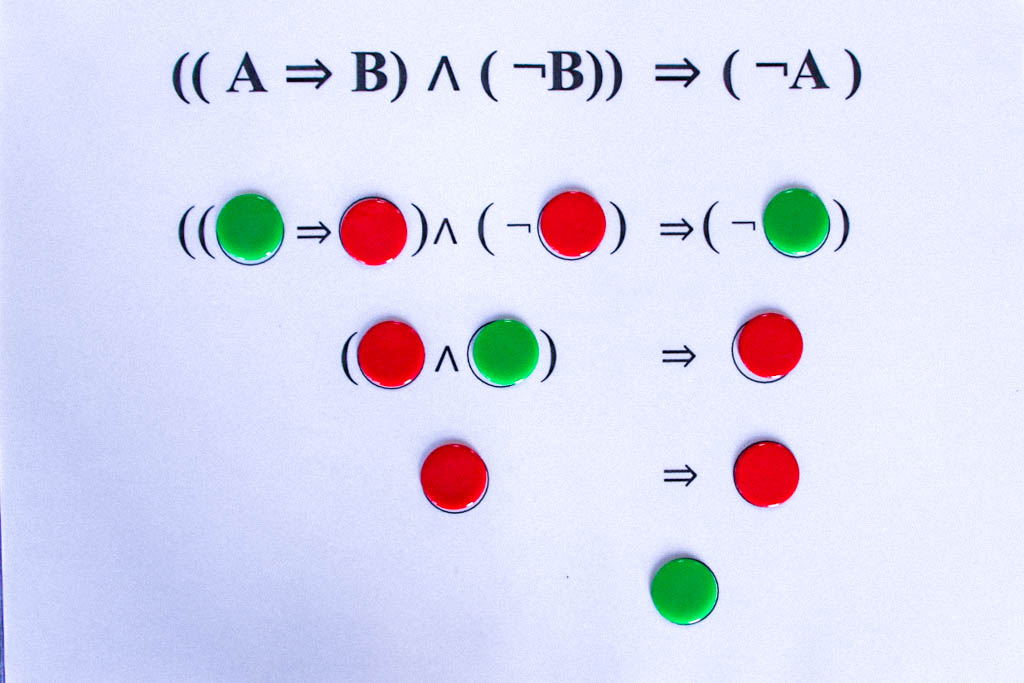Wie können wir helfen?
So friedlich kann es nur im Paradies zugehen: Alle Tiere leben einträchtig miteinander. In unserem Exponat wurden die paradiesischen Zustände mithilfe der schönen Tiere der Firma Schleich hergestellt. Es gibt ein grün umzäuntes Gehege links und ein weiß eingezäuntes Gehege rechts. Die beiden Gehege umschließen auch einen gemeinsamen Bereich. Die grün umzäunte Menge enthält alle vorhandenen gefiederten Tiere, alle zur Verfügung stehenden Haustiere befinden sich in der weiß gekennzeichneten Menge. In der Schnittmenge – { gefiederte Tiere }∩{ Haustiere } – sind diejenigen Figuren, die sowohl Haustiere sind als auch Federn haben. Alle anderen zur Verfügung stehenden Tierfiguren gehören weder zur Menge A={ gefiederte Tiere } noch zur Menge B={ Haustiere }, sie gehören zur Restmenge und befinden sich außerhalb von jeder der beiden Mengen.
Natürlich kann es auch vorkommen, dass die Schnittmenge zweier Mengen A und B leer ist. Sortieren wir z.B. die vorhandenen Tiere entsprechend so ein, dass A={ Federtiere } und B={ Säugetiere } gilt, dann gibt es kein Element in der Schnittmenge, die Schnittmenge ist damit leer: A∩B={ }:
Unten steht der intelligente Linus grübelnd vor der schwarzen Schultafel, auf der weiß auf schwarz schematisch die sieben möglichen Schnittmengen von drei Mengen A, B und C dargestellt sind:
Diejenigen, die in den Genuss “der Mengenlehre” in ihrer Schulzeit gekommen sind, erkennen hier ein Diagramm für zwei Mengen A und B. Die Elemente sind hier die verschiedenen Tiere. Die Menge A besteht aus allen gefiederten Tieren und die Menge B aus allen Haustieren. Die gefiederten Tiere befinden sich im grünen Gehege und die Haustiere im weißen Gehege. Logisch befinden sich dann alle gefiederten Haustiere im dem Bereich des Geheges, der sowohl zum grünen als auch zum weißen Gehege gehört: Diesen Sektor nennt man die Schnittmenge A und B, symbolisch mit A∩B. Sie enthält alle Elemente, die sowohl zur Menge A als auch zur Menge B, d.h. die zur Menge A und zur Menge B gehören. Die Vereinigungsmenge A∪B enthält alle Elemente, die sich im gesamten Gehege befinden, d.h. im Beispiel alle Tiere, die gefiedert oder Haustiere sind. Wie immer in der Mathematik ist das “Oder” hier nicht im ausschließenden Sinne von dem “Entweder-oder” gemeint. Die anderen Tiere bilden die Restmenge – sie befinden sich in keinem der beiden Gehege. Alle Tiere, die insgesamt für dieses Experiment zur Verfügung stehen, bilden die Grundmenge an Tieren.
Mit der Neuen Mathematik bezeichnet man eine internationale Strömung, mit der eine Reformierung des mathematischen Unterrichts in den 1960er und 1970er in Gang gesetzt wurde. Sie lief in den USA unter dem Namen New Math. Ziel war es, den traditionellen Rechenunterricht in der Schule durch die Beschäftigung mit abstrakten Strukturen zu lehren. Die Neue Mathematik sollte die Entwicklung in der wissenschaftlichen Mathematik nachvollziehen, die dort in den Jahrzehnten um 1900 mit der Hinwendung zu axiomatischer Grundlegung und mengentheoretischer Formulierung der Mathematik erfolgte. Parole “Nieder mit Euklid – Tod den Dreiecken!” Eines der Motive war sicher auch der sog. Sputnik-Schock, der auf einen großen Nachholbedarf im Westen hinzuweisen schien. In der Bundesrepublik war von einem “Bildungsnotstand” die Rede.
Es regte sich aber auch zunehmend Kritik an der grundlegenden Reform (=Revolution?). Erwartete Erfolge blieben aus, Widerstände wuchsen und so schrieb beispielsweise 1973 Morris Kline sein erfolgreiches Buch Why Johnny can’t add. The failure of the New Math.
Genauso ratlos und wenig begeistert – wie oben Linus – reagierten auch viele Schüler und Lehrer, insbesondere aber auch viele Eltern auf die große revolutionäre Erneuerung des Mathematikunterrichts. Sicher hat diese Reformbewegung auch zu Verbesserungen des Mathematikunterrichts geführt, aber auch zu viel Frust und Rückschlägen.
Da verführen die bei Kindern so beliebten kleinen Plastiktierchen schon eher zu begrifflichen Mengenbildungen, wie dieses Experiment der Mathothek zeigt. Dazu kommt, dass hier fächerverbindend begriffliches Denken spielerisch mit Wissen aus der Biologie verknüpft werden kann.
Es gibt weitere Kärtchen mit Vorschlägen für weitere Mengenbildungen, z.B. Pflanzenfresser und Wildtiere, Huftiere und Nutztiere, Vögel und Pflanzenfresser usw. Natürlich kann sich jeder auch selbst geeignete Kategorien ausdenken.
Zum Thema Mengenlehre und dem Versuch, mit der Bewegung von NEW MATH den Mathematikunterricht zu reformieren, gibt es einige weitere Exponate in der Mathothek, z.B. ein Taschenbuch aus dem Jahr 1970, das vom Rowohlt Verlag veröffentlicht wurde. Sein Titel lautete Revolution im Rechenbuch – Die Mathematik verliert ihre Schrecken. Die Formulierung des Titels sagt viel über die großen Erwartungen dieser Reformversuche aus.
Entsprechende Unterrichtsmaterialien für die Schüler wurden von den Schulen angeschafft, beispielsweise das vom Schrödel-Verlag herausgegebene Begriffsspiel matema, bei dem es um die Merkmale Form, Farbe und Größe geht.
Ein Beispiel für den Versuch, einen stärker spielerischen Zugang zur Mengenlehre zu bieten, war das inzwischen vom Flohmarkt stammende Spiel Lustige Mengenlehre:
Solche Angebote kamen wohl besonders gut bei vielen Eltern an. Da für sie die “moderne Mathematik” meist auch Neuland war, versuchten sie durch solche und ähnliche Angebote ihre Kinder – ohne die eigenen entsprechenden Kenntnisse zu haben – zu unterstützen. Vielleicht können Euch diese Kartenbilder bereits gewisse Vorstellungen zu diesem Mengenlehre-Spiel vermitteln.
Diese beiden Karten sind ein Beispiel für zwei Karten, bei denen die linke Karte eine Beschreibung in vier Merkmalen ist und die rechte Karte die entsprechende Konstellation umkehrbar eindeutig darstellt. Die folgenden acht rechten Karten zeigen weitere Beispiele für mögliche Konstellationen von jeweils vier Merkmalen:
Jahre nach dem Höhepunkt der Neuen Mathematik erlebte ich Schülergruppen, die mit einer großer Begeisterung ein Kartenspiel mit dem Namen SET! spielten. Auf den ersten Blick erschien es mir, dass es dabei auf schnelle Reaktionsfähigkeit ankomme. Aber nach entsprechender “Einweihung” erkannte ich, dass auch hier eine “Mengenlehre-Spiel-Struktur” vorlag.
Dieses Kartenspiel besteht aus 81 Karten, die alle verschieden sind. Sie unterscheiden sich in den abgebildeten Symbolen, und zwar in der Menge (1, 2 oder 3), Farbe (rot, violett oder türkis), Form (Oval, Rechteck oder Welle) und der Füllung (leer, halb oder voll). Das Spiel beginnt mit einem gut gemischten Stapel der 81 Karten. Es werden dann die obersten 12 zu einem 4×3-Rechteck ausgelegt. Alle Spieler suchen dann gleichzeitig nach einem Set und nehmen dieses an sich. Wer ein Set erkannt zu haben glaubt, sagt dies laut und – wenn es richtig ist – nimmt er es an sich. Im anderen Falle muss er solange aussetzen, bis ein anderer ein richtiges Set gefunden hat. Die gewonnen Sets stapelt man verdeckt bis zum Spielende. Die als gewonnenen Sets entfernten Karten werden von einem beliebigen Spieler durch die nächsten drei Karten vom Stapel ergänzt. Gibt es unter den 12 ausgelegten Karten kein Set, so werden zum Weiterspielen einfach drei Karten vom Stapel ausgelegt. Es gewinnt, wer die meisten Karten gesammelt hat. Ein Set besteht immer aus drei Karten und zeichnet sich dadurch aus, dass jede der vier Eigenschaften – jeweils für sich betrachtet – entweder genau gleich oder völlig verschieden ist.
Beispiele für Sets:
Zwei weitere Beispiele, wobei das linke kein Set und das rechte ein weiteres Beispiel für ein Set ist:
Vielleicht ist hier im Zusammenhang mit Set! ein weiteres Objekt der Mathothek interessant, nämlich das Dopple-Spiel und seine Beziehung zur projektiven Ebene.
Ein weiteres Objekt, das mit Mengenlehre und Verknüpfungstafel zu tun hat, ist in der Mathothek entstanden:
Neben diesen mehr spielerischen Exponaten zur “Mengensprechweise” gibt es in der Mathothek eine reiche und anspruchsvolle Reihe von Objekten, die einige der u.a. von Cantor wesentlichen Erkenntnisse zur eigentlichen Mengentheorie und anderen Grundlagenfragen gut zugänglich machen können.
Verschiedene Kategorien des Unendlichen, wie z.B. die Abzählbarkeit der Menge der natürlichen und der rationalen Zahlen, der Überabzählbarkeit der reellen Zahlen, aber auch den logischen Problemen der eigentlichen Mengentheorie:
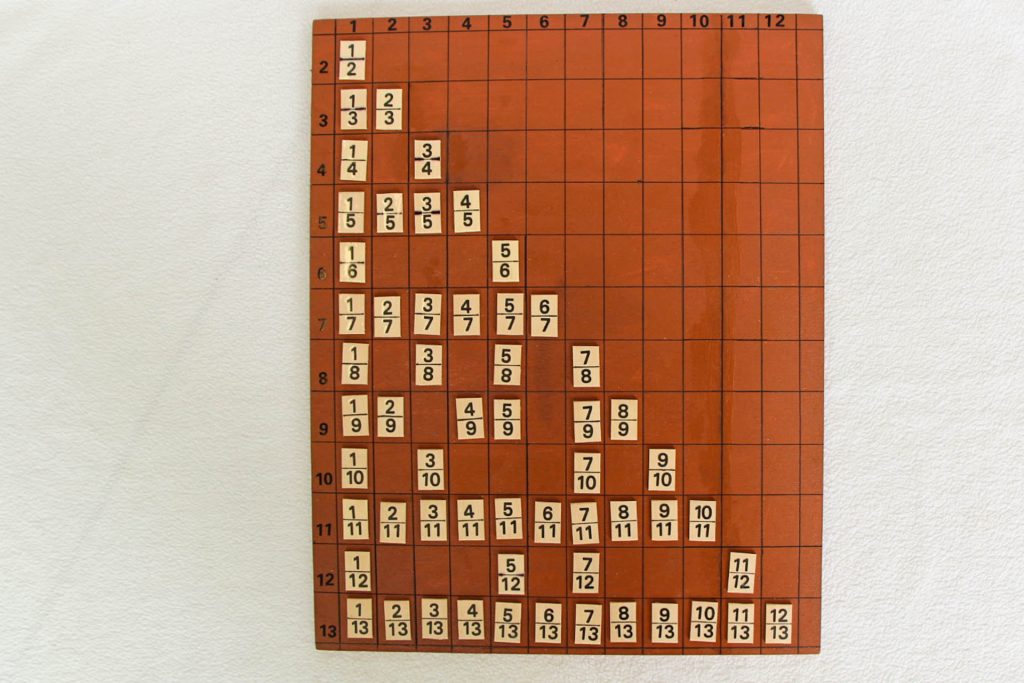
Aber auch viele logische Probleme im Zusammenhang mit der Mengentheorie sind durch geeignete Experimente in der Mathothek erfahrbar, so das Dilemma der Menge, die alle Mengen enthält, die sich nicht selbst als Teilmenge enthalten, das berühmte Barbierproblem:
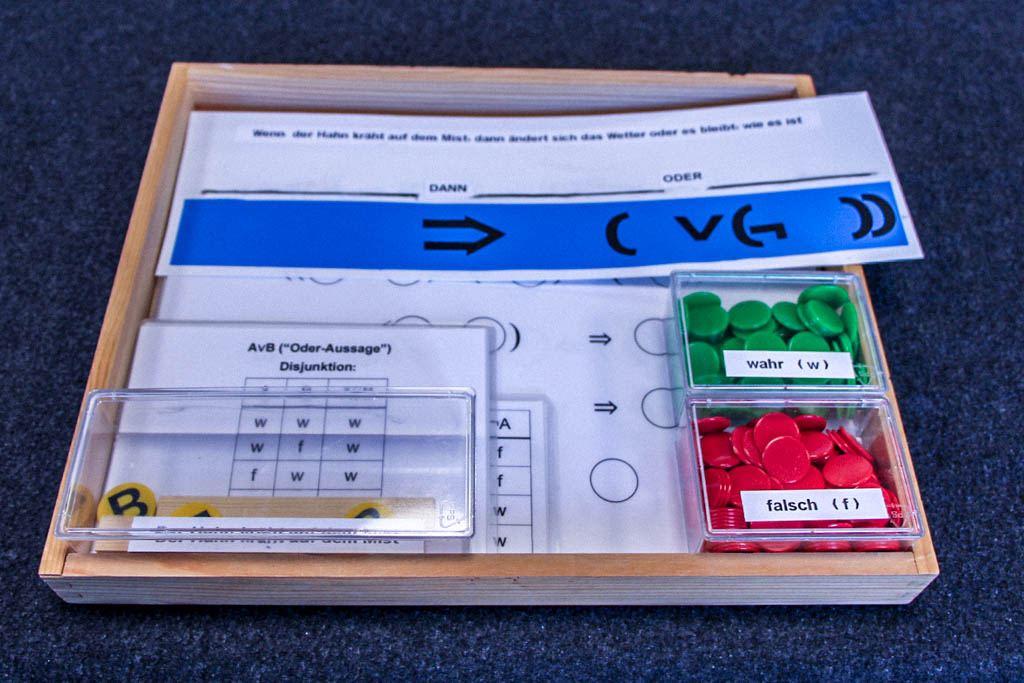
Natürlich sind die logischen Operationen, die mit dieser “Mengenlehre” eng verbunden sind, heute im Zeitalter des Computers besonders interessant und grundlegend, z.B. die formalisierte Junktorenlogik, d.h. der klar geregelte Umgang mit den Junktoren “und”, “oder”, “wenn-dann”, “nicht” usw. Hierzu gibt es ein interaktives Exponat in der Mathothek:
