Mathothek

168 = 169  

Ein Zaubertrick?

Oder muss die Mathematik Insolvenz anmelden?

Läge hier kein “fauler Zauber” vor, würde das gesamte Gebäude der Mathematik zusammenstürzen. Wäre diese falsche Aussage ableitbar, ließe nach den Gesetzen der Logik jede Aussage herleiten. Mit der Aufhebung der Widerspruchsfreiheit wäre das Ende der Mathematik gekommen.
Wenn ein Quadrat der Seitenlänge 13 – wie oben abgebildet – zerschnitten wird, und dann die Teile zu einem Rechteck der Seitenlängen 8 mal 21 zusammengesetzt werden, stellt man Folgendes fest:
Der Flächeninhalt ergibt für das Quadrat A = 13 · 13 = 169,
für das Rechteck allerdings nur A = 8 · 21 = 168. Zauberei?

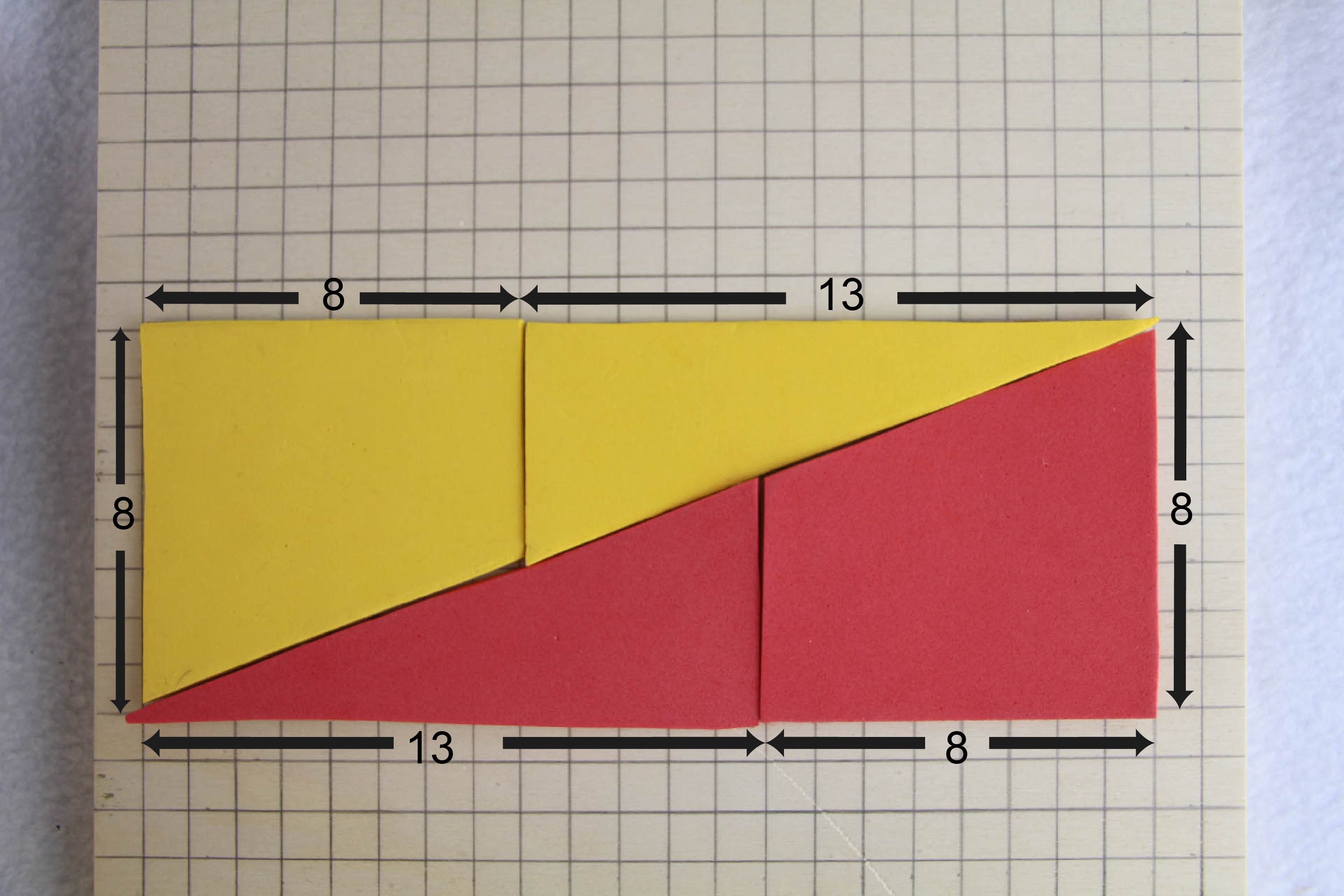
Die Erklärung liegt darin, dass die “Diagonale” des Rechtecks keine Gerade ist. Berechne dazu die Steigungen der einzelnen Diagonalenstücke. ( m₁ = 5/13 und m₂ = 3/8).    

Das Kunststück funktioniert auch mit jedem anderen Quadrat, dessen Seitenlänge eine Fibonacci-Zahl (f_n = 1, 1, 2, 3, 5, 8, 13, 21, …) ist, die größer als zwei ist. Da f_n = f_n−2 + f_n−1, können wir das Quadrat wie angegeben aufteilen und wieder zu einem Rechteck zusammensetzen.

Bei zu kleinen Fibonacci-Zahlen “riecht man den Braten” zu schnell.

Dieses Exponat hat mit vielen anderen in der Mathothek die Aufgabe, den Besucher auf die Gefahren einer nur auf Anschauung beruhender Vermutung zu warnen. Erst durch die rationale Analyse und logische Überprüfung kommt man zur gesicherten Erkenntnis.