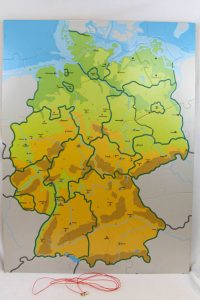
Bei diesem Exponat gibt es eine relativ große physikalische Karte der Bundesrepublik Deutschland. In den eingetragenen Städten sind kleine Ringschrauben eingedreht worden. So sind auch alle 16 Hauptstädte der Bundesländer zu finden. Außerdem ist noch eine rote Kordel vorhanden, die am Anfang und am Ende einen kleinen Ring hat. Daraus ergibt sich die Aufgabe: Versuche eine Rundreise durch die 16 Länderhauptstädte zu machen und finde mit den Luftlinienverbindungen zwischen den Städten den kürzesten Streckenzug heraus. Nimm ruhig Wiesbaden als Anfangs- und Endpunkt der Reise. Die rote Kordel muss reichen. Du merkst sehr bald, dass die Strategie, immer zu der am nächsten gelegenen Hauptstadt zu gehen, nicht zur kürzesten Rundreise führt.
Nimm an, Du würdest alle Entfernungen zwischen den einzelnen Städten (Tabelle) wissen und Du rechnetest für alle möglichen Kombinationen die Länge der Rundreisen aus, so wären das bereits 650 Mrd. Ergebnisse, d.h. so viele Rundreisen durch die 16 Hauptstädte wären insgesamt möglich. Um diese 650 Mrd. Längen zu berechnen und zu vergleichen, da hätte auch ein moderner Computer ein paar Jahre Rechenarbeit!
Du kannst das obige Experiment natürlich auch mit mehr oder weniger Städte Deiner Wahl versuchen. Das Problem wächst überwältigend an, je mehr Städte auf der Rundreise liegen.
Es handelt sich hier um ein kombinatorisches Optimierungsproblem. Es gibt bisher keine Formel, was angesichts der Komplexität des Problems auch nicht zu erwarten ist, sondern nur Lösungsverfahren – Algorithmen – die schrittweise recht gute Näherungsergebnisse liefern. Solche Optimierungen sind wirtschaftlich hoch interessant. Aus diesem Grund ist das Travelling Salesman-Problem das am intensivsten untersuchte kombinatorische Optimierungsproblem und nach wie vor eine große Herausforderung:
→ Zur Lösung
Bei einer Lösung erwarte ich neben der grafischen Lösung noch die Länger der Strecke. Na gut, habs gemacht. Mich hat interessiert, wie lang die kürzesteste Menschenkette durch alle Bundesländer wäre. Mit dem Kompromiß, dass die Kette durch die Hauptstädt der Bundesländer geht kann ich leben. Bei Google Maps ergibt die oben dargestellte Strecke zu Fuß und ohne Fähren eine Länge von 2434 km. Wenn man jetzt eine Menschenkette bilden würde nach dem Vorbild der Kette von Ulm nach Stuttgart 1983, dann braucht man bei 1m pro Mensch schlappe 2 Millionen Vierhundertvierunddreißigtausend Menschen. Wer berechnet das Ganze jetzt unter der Bedingung, dass nur jedes Bundesland verbunden sein muss, ohne dass die Hauptstadt beteiligt ist?