Wie können wir helfen?
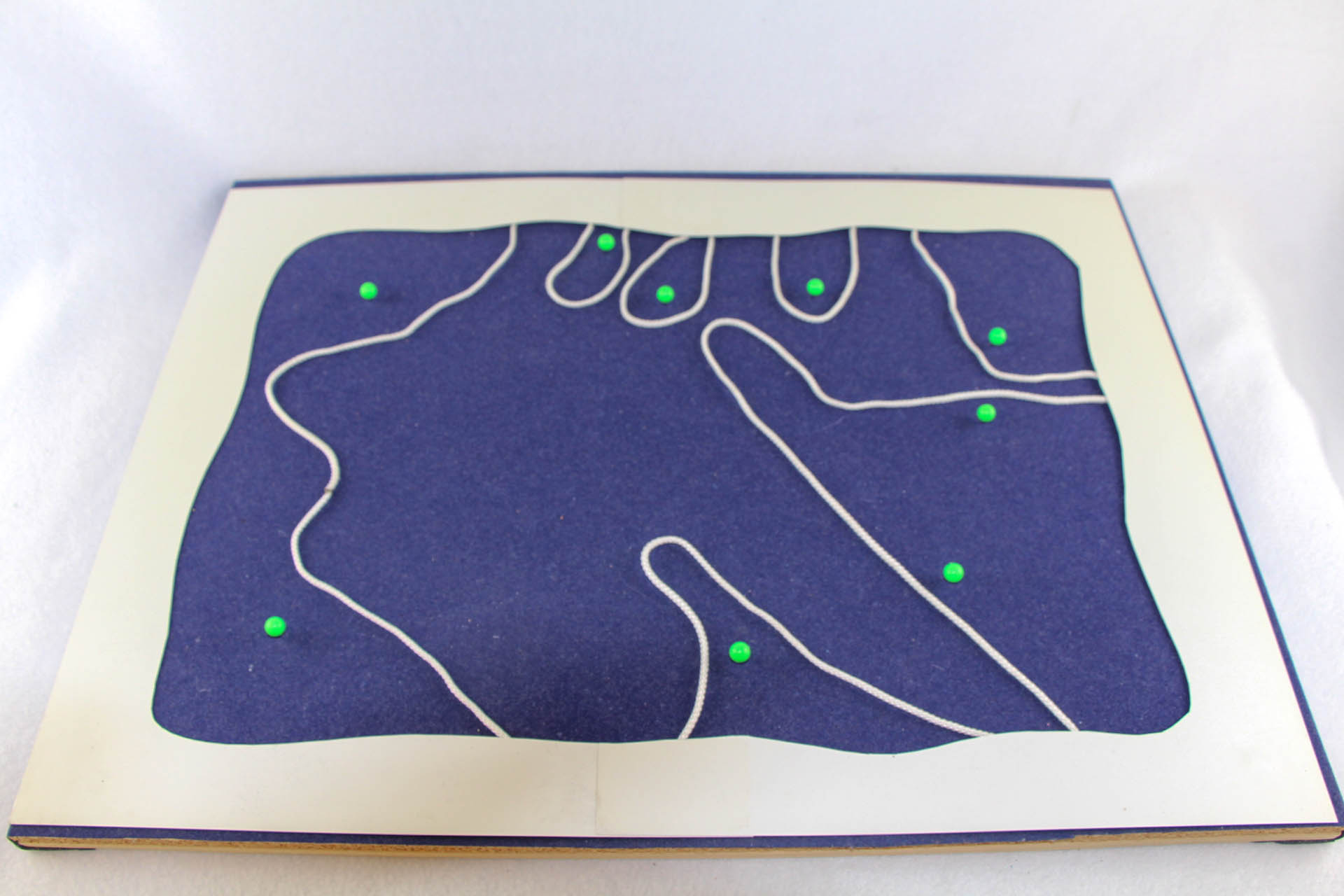
Dieses Exponat der Mathothek besteht aus einer Korkplatte, die mit einer blauen gerauten Folie überzogen wurde, einer geschlossenen weißen Kunststoffkordel und einigen farbigen Pinnadeln. Es dient dazu, den Inhalt des folgenden Satzes auf interessante Art und Weise begreifbar zu machen:
Jede einfache, geschlossene, ebene Kurve, Jordan’sche Kurve (hier die weiße, zusammengeklebte Kordel), zerlegt die Ebene in zwei disjunkte Gebiete, die von ihr getrennt werden. Die Vereinigung der beiden Gebiete und der Kurve ergibt die gesamte Ebene.
Das Exponat in der Mathothek lässt diesen Sachverhalt auf folgende Weise erfahrbar machen: Steckt man die vorhandenen Nadeln so in die blaue Fläche, dass zwei Nadeln auf ihrer geraden Verbindungsstrecke immer durch eine gerade Anzahl weißer Kordelstücke getrennt sind, dann stecken die Nadeln alle in einem Gebiet. Durch den weißen Kunststoffrahmen ist die Vorführung für den Zuschauer besonders spannend, weil beim Wegziehen der Kordel entweder alle Nadeln innerhalb der Kordel hängen bleiben, oder die Kordel sich widerstandslos herausziehen lässt.
Hier ist ein Beispiel für eine solche Vorführung: