In der Mathothek gibt es zwei Exponate, die auf den ersten Blick wie lateinische Quadrate aussehen, aber dann doch keine sind. Praktisch in jeder Zeile und Spalte findet man Zahlen oder Symbole, die mehrfach vorkommen. Das widerspricht der Forderung, dass bei einem lateinischen Quadrat mit n Zeilen und n Spalten in jeder Zeile und jeder Spalte alle n Symbole genau einmal auftreten dürfen. In der Mathothek gibt es sehr viele Exponate zum Thema solcher lateinischen Quadrate mit den verschiedensten Zusatzbedingungen. Hier ein einfaches Beispiel für ein lateinisches Quadrat:
Jede der acht Farben kommt in jeder Zeile und jeder Spalte mindestens einmal vor, es tritt aber auch keine Farbe mehrfach auf. Bei unserem 8×8-Quadrat sind beide Bedingungen verletzt: Zahlen treten in Zeilen und Spalten mehrfach auf, aber es kommen dann auch nicht alle acht Zahlen in diesen Zeilen und Spalten vor.
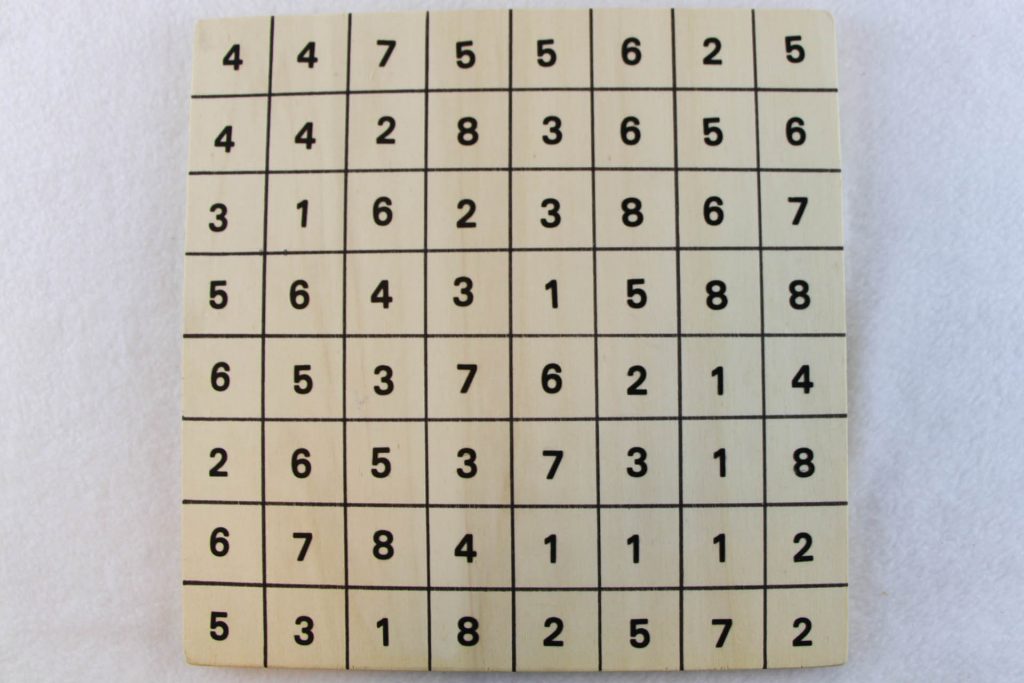
Die 8×8-Matrix mit den Zahlen 1, 2, 3, 4, 5, 6, 7, 8 sieht so aus:
Die Aufgabe besteht nun nicht darin, daraus ein lateinisches 8×8-Quadrat zu machen, sondern die „Doppelgänger“ zu beseitigen, sodass in jeder Zeile und jeder Spalte jede der acht Zahlen höchstens einmal vorkommt. Dabei soll die Anzahl der entfernten Zahlen minimal sein.
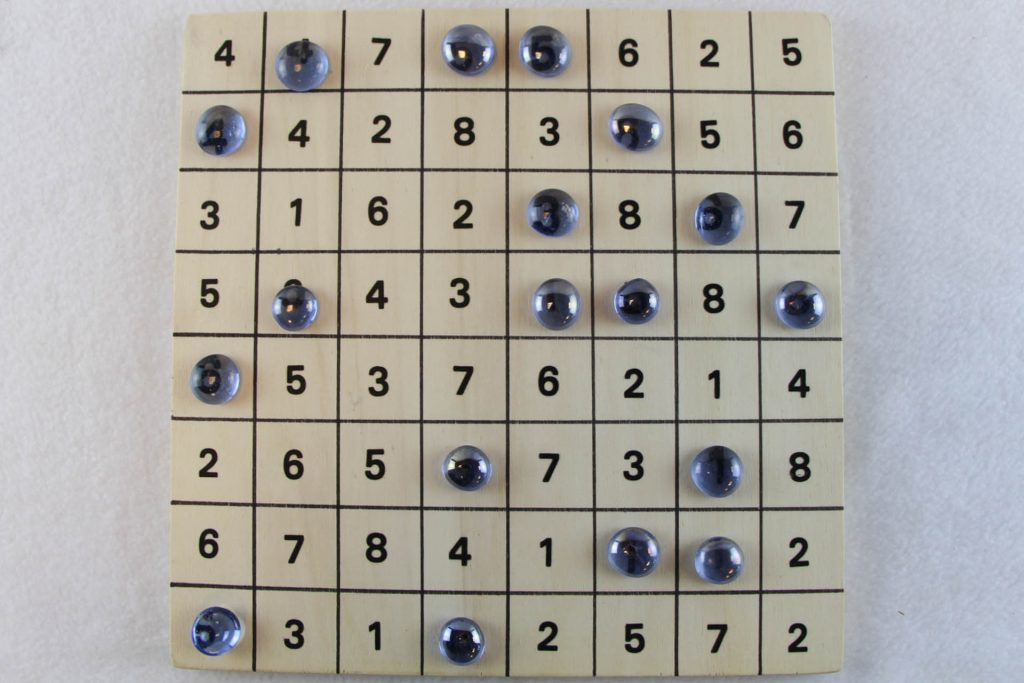
Die blauen Glasnuggets dienen dazu, diejenigen Zahlen zu markieren, die man entfernen möchte.
Bei der zweiten Logelei geht es nicht um Zahlen, sondern um Symbole für Drei- und Vierecke: rechtwinkliges Dreieck, gleichseitiges Dreieck, Parallelogramm, Raute oder Rhombus, Rechteck, Quadrat und Trapez.
Auch hier handelt es sich um ein „fehlerhaftes“ lateinisches Quadrat, denn es kommen in allen Zeilen und Spalten die sieben geometrischen Formen nicht alle vor, weil in jeder Zeile und jeder Spalte manche mehrfach vorkommen. Die Aufgabe besteht auch hier darin, die „Doppelgänger“ bis auf ein Individuum zu „schwärzen“, d.h. mit einem schwarzen Chip zu belegen. Allerdings gilt nicht nur die Regel, möglichst wenige Felder zu schwärzen, sondern zusätzlich darauf zu achten, dass keine orthogonal benachbarten Felder geschwärzt werden und dass die nicht geschwärzten Felder zusammenhängen.
Die Lösungen erhältst Du durch Vergrößerung der Fotos: