(Link öffnet in neuem Tab/Fenster)
Der Zusammenhang der Anzahl der Flächen, Kanten und Ecken eines Körpers sind nicht willkürlich. Allerdings muss es hier ein Körper sein, der ein Polyeder mit gewissen Eigenschaften ist. Das hat nun noch gar nichts mit planaren Graphen zu tun. Folge der Umleitung – und wie so oft bei Umleitungen erfährt man auf diese Weise mehr als auf dem direkten Weg.
Ein Polyeder (Vielflächner) ist ein geometrischer Körper, der allseits von ebenen Flächen (Polygonen, Vielecken) begrenzt ist. Die Seitenflächen schneiden sich in den Kanten, diese stoßen in den Ecken zusammen.
Ein Polyeder ist konvex, wenn folgendes wahr ist: Gehören die Punkte A und B zum Polyeder, dann gehört auch immer deren Verbindungsstrecke zu dem Polyeder. Beschränkt ist ein Polyeder, wenn seine Ecken alle innerhalb einer Kugel mit endlichem Radius liegen.
Für jedes beschränkte und konvexe Polyeder gilt folgende Behauptung: „Die Anzahl der Flächen F plus die Anzahl der Ecken E ist gleich der Anzahl der Kanten K plus 2“, als Formel: F+E=K+2. Dieser mathematische Satz heißt nach dem berühmten Mathematiker Leonhard Euler Euler’scher Polyedersatz. 1750 erwähnte Euler diese Erkenntnis zuerst in einem Brief an den Mathematiker Goldbach und 1758 veröffentlichte er einen Beweis. Inzwischen gibt es viele verschiedene Beweise.
Beispielhaft seien hier die platonischen Körper betrachtet:
Dodekaeder F=12, E=20, K=30
Hexaeder F=6, E=8, K=12
Tetraeder F=4, E=4, K=6
Oktaeder F=8, E=6, K=12
Ikosaeder F=20, E=12, K=30
Für jeden der fünf platonischen Körper bestätigt sich der Euler’sche Polyedersatz: F+E=K+2.
In der Mathothek stehen sehr, sehr viele beschränkte, konvexe Polyeder zum Experimentieren zur Verfügung. Man kann Flächen, Ecken und Kanten abzählen und das Ergebnis überprüfen, oder man zählt zwei Kategorien und berechnet mit der eulerschen Formel die dritte.
_____________________________________________
Zu jedem beschränkten und konvexen Polyeder mit einem zusammenhängenden Inneren ohne Löcher gibt es einen entsprechenden planaren Graphen, durch den die Beziehungen seiner Flächen, Kanten und Ecken dargestellt werden können. Dabei ist ein planarer Graph ein ebenes, zusammenhängendes Netz, dessen Kanten einander nicht schneiden.
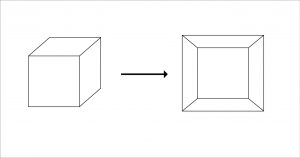
Dies kann man sich wie folgt am Beispiel eines Würfels veranschaulichen
Oben sieht man (im Schrägbild) einen Würfel, dann rechts davon die Projektion des Würfels in die Ebene. Der Bodenfläche des Würfels entspricht nun das große Quadrat. Diese zweite Figur ist dann aber kein planarer Graph. Das wird erst einer, wenn wir die gesamte Fläche außerhalb des großen Quadrats als weitere Fläche für den planaren Graphen des Würfels dazu nehmen. Jetzt hat der entstandene Graph wie der Würfel sechs Flächen, 12 Kanten und acht Ecken. An jeder Ecke treffen drei Kanten zusammen usw. Außerdem sind die Beziehungen zwischen den Flächen, Kanten und Ecken erhalten geblieben, vor allem auch F+E=K+2!
_______________________________________
Euler’scher Polyedersatz für planare Graphen.
Dieses Exponat besteht aus einer blau überzogenen Korkplatte, einer weißen geschlossenen Kordel und drei Kästchen mit gelben, roten und blauen Pinnadeln. Mit einer weißen Kordel lässt sich ein planarer Graph legen. Mit den gelben Pinnadeln werden die Flächen, mit den roten die Ecken und mit den blauen die Kanten markiert. Hat man keinen Fehler gemacht, wird die Euler’sche Polyederformel
F+E=K+2
wiedermal bestätigt, bzw. umgekehrt: Wenn das Ergebnis unseres Experiments die Gleichung erfüllt, haben wir keinen Fehler gemacht. Hier ein Beispiel.
Schritt für Schritt:
Man muss wahrlich kein Algebra-Champion sein, um den Euler’schen Polyedersatz umzuformen, z.B. in F+E-K=2, K=F+E-2, F=K-E+2 oder E=K-F+2. Die letzten drei Formeln können dazu dienen, die Anzahl der Kanten, Flächen oder Ecken zu berechnen, wenn die beiden anderen Anzahlen bekannt sind.
Die Mathothek ist ein Schlemmertempel mit mathematischen Köstlichkeiten und keine Kantine mit Standardmenue.
.