Mathothek

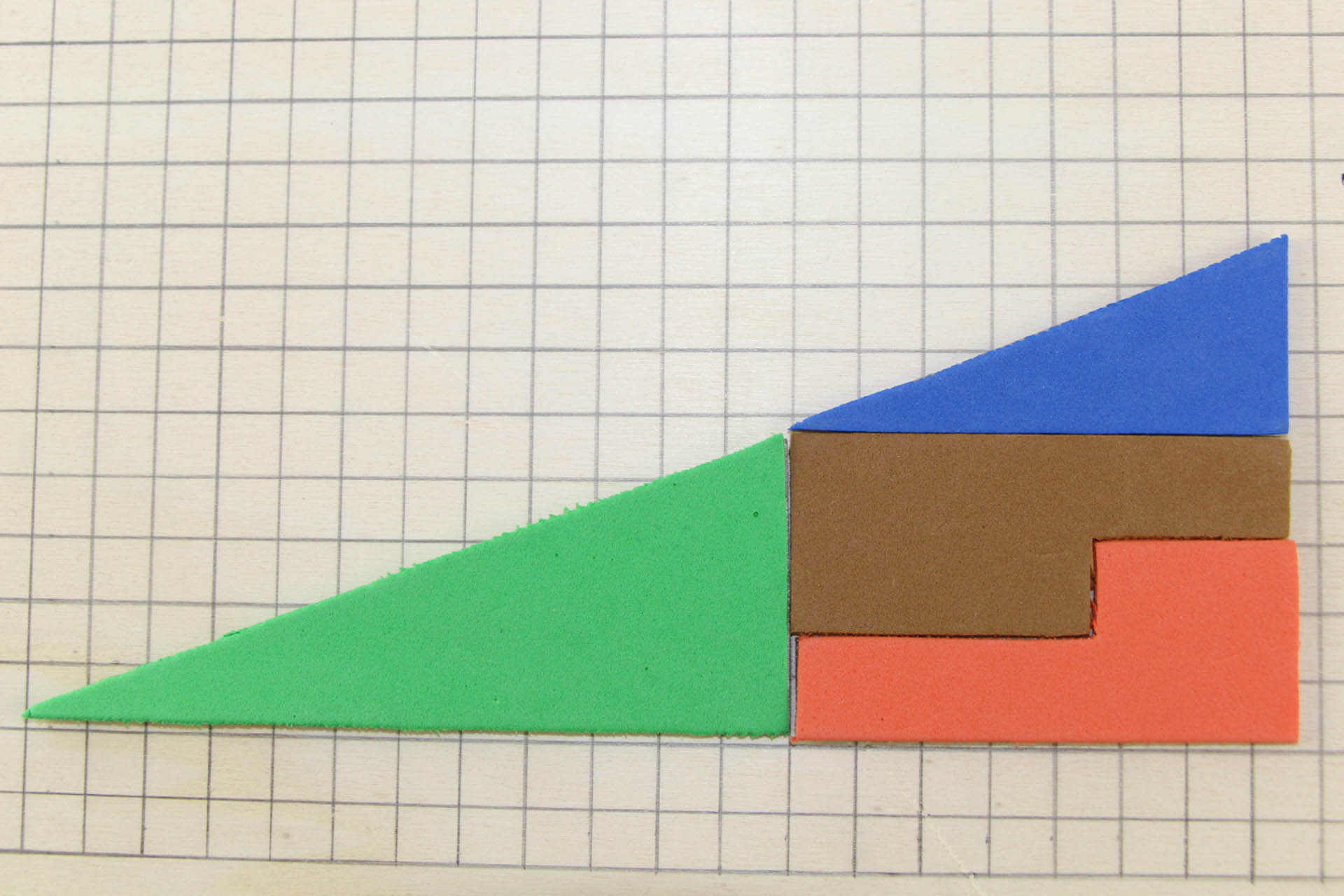
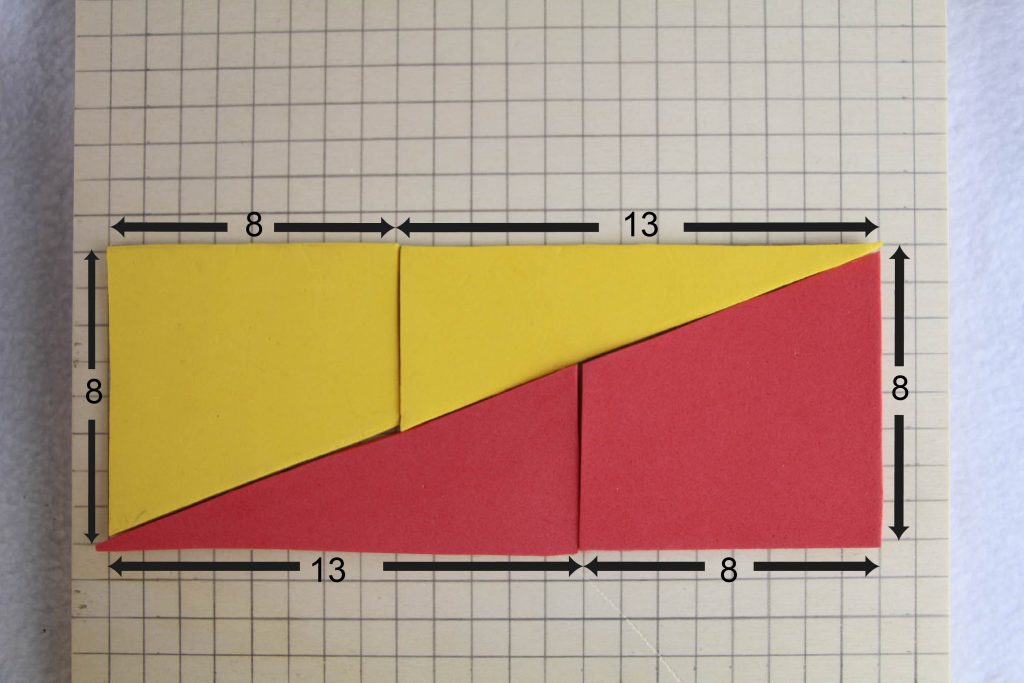
“Das verschwundene Quadrat”-Rätsel ist eine optische Täuschung aus der Geometrie. Es scheint so, als ob die Fläche des Dreiecks unterschiedlich groß sei, je nachdem, wie man die einzelnen Teilflächen anordnet. Dabei sind die vier Teildreiecke paarweise deckungsgleich. Das Rätsel stammt vermutlich von dem amerikanischen Amateurzauberer Paul Curry (1953).

Läge hier kein “fauler Zauber” vor, würde das gesamte Gebäude der Mathematik zusammenstürzen. Wäre diese falsche Aussage ableitbar, ließe nach den Gesetzen der Logik jede Aussage herleiten. Mit der Aufhebung der Widerspruchsfreiheit wäre das Ende der Mathematik gekommen.

Die Erklärung liegt darin, dass das blaue und das grüne Dreieck nicht ähnlich sind und die Steigungen des blauen und des grünen Dreiecks somit nicht gleich sind, nämlich blau 3/7 und grün 5/12). Also ist die Verbindung der beiden spitzen Ecken des großen “Dreiecks” in beiden Fällen keine Gerade. Bei dem größeren (linken) Pseudodreieck vergrößert der “Knick” die Dreiecksfläche, bei dem kleineren “Dreieck” verringert der “Knick” den Flächeninhalt.

Dieses Exponat hat mit vielen anderen in der Mathothek die Aufgabe, den Besucher auf die Gefahren einer nur auf Anschauung beruhender Vermutung zu warnen. Erst durch die rationale Analyse und logische Überprüfung kommt man zur gesicherten Erkenntnis.

Weitere Experimente findest Du unter “Einer geht noch”.