

Was haben „die sieben Brücken in Königsberg“, das „Haus des Nikolaus“ und eine Führung durch das Fundament eines neuen Hauses miteinander zu tun?
Mit dem Brückenproblem hat es angefangen. Dem großen Mathematiker Leonhard Euler, der viele Jahre am Hofe der russischen Zarin Katharina der Großen in St. Petersburg wirkte, wurde die Frage gestellt, ob man einen Spaziergang so machen könne, dass man genau einmal über jede der sieben Brücken über den Pregel gehen könne und wieder auf dem Festland ankomme. Euler verneinte diese Frage und wurde zum Begründer der Graphentheorie, aber nicht nur das.
Beim Haus des Nikolaus geht es darum, die fünf kleinen Nägel mit einem Faden in einem Zug zu verbinden. Dabei ist es entscheidend, dass dies so erfolgt, dass keine Verbindung mehr als einmal benutzt wird. (Natürlich kann man das auch mit Papier und Bleistift machen, wäre aber in der Mathothek uncool.) Die Meisten erinnern sich, dass es relativ leicht möglich ist, zumal wenn man auch noch die Silben des bekannten Reimes „Das ist das Haus vom Ni-ko-laus“ dabei murmelt.
Im dritten Fall baut eine junge Familie ein Eigenheim. Allerdings sind gerade mal die Grundmauern zu sehen. Der stolze Bauherr will Besuchern nun das neue Haus vorführen. Dazu möchte er alle Räume zeigen und dabei durch jede Tür – auch durch die Haustür und die Terrassentüren – genau einmal schreiten. So kommen wir „dem Kern des Pudels“ schon ein großes Stück näher. Wir haben in jedem der drei Fälle Wege oder Verbindungen und Punkte oder Landflächen oder Räume. In der Graphentheorie nennt man die Ersteren „Kanten“ und die Letzteren „Ecken“. Die drei gestellten Aufgaben lassen sich dann übersichtlich als Graphen darstellen und die Fragen bzw. Aufgaben leicht beantworten bzw. lösen.
Analysieren wir exemplarisch das Königsberger Brückenproblem:
Die Frage lautete: „Kann man einen Rundgang über alle sieben Brücken machen, dabei über jede Brücke genau einmal gehen und wieder am Ufer ankommen?

Leonard Euler hat die Frage verneint. Auch Du wirst keinen solchen Weg finden – egal welchen Weg Du versuchst. Entweder Du bleibst auf einer Insel hängen, oder Du kannst die Brücke zwischen den Inseln vergessen.
Hier ist der Graph zu dem Brückenbild:
Die linke Ecke (=Punkt) entspricht der linken Insel, die rechte Ecke der rechten Insel. Die beiden anderen Ecken entsprechen den beiden Ufern, die Kanten (= Verbindungslinien) sind die Brückenwege.
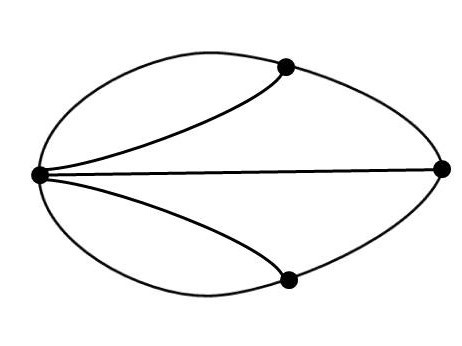
Was dabei auffällt ist, dass an einer Ecke fünf Kanten ankommen und an den anderen drei Ecken jeweils drei Kanten enden. An allen Ecken endet eine ungerade Anzahl Kanten. In dem Falle ist der Graph kein Eulerkreis. Es gibt keinen solchen gewünschten Rundweg. Überlege Dir z.B., willst Du auf eine Insel und wieder herunter – ohne eine Brücke zweimal zu benutzen – so benötigst Du eine gerade Anzahl von Brücken.

Hier haben wir eine Hilfsbrücke zwischen den beiden Inseln zur Verfügung. Jetzt können wir jedenfalls nicht mehr auf einer Insel hängen bleiben. Allerdings endet unser einmalige Spaziergang über jede Brücke nun auf der anderen Seite des Pregels. Unten ist der dazugehörige Graph. Der neuen Verbindungsbrücke entspricht die blaue Kante. Dieser Graph besitzt nur zwei Ecken, an denen eine ungerade Anzahl Kanten endet. Das ist dieselbe Situation wie beim „Haus vom Nikolaus“. In beiden Fällen spricht man einem nicht-geschlossenen Eulerkreis.
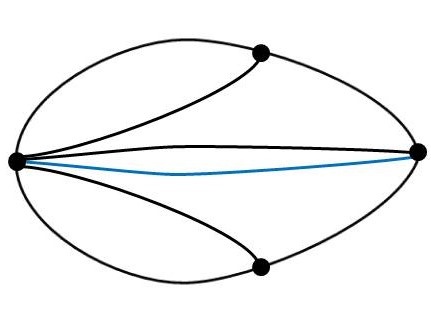

In diesem Fall haben wir zwei Belfsbrücken für unsere Königsberger Flaneure errichtet. Jetzt können sie – falls kein Hochwasser die Trittsteine wegschwemmt – ihren gewünschten Rundgang machen und am Startufer wieder ankommen. Der dazugehörige Graph sieht diesmal so aus:
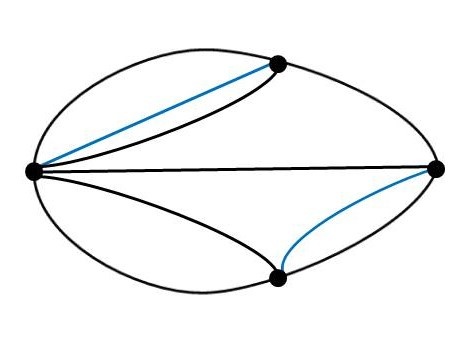
Jede Ecke besitzt nun eine gerade Anzahl Kanten, und zwar sechs oder vier. Es handelt sich um einen geschlossenen Eulerkreis. Ein geschlossener Eulerkreis lässt sich „in einem Zug zeichnen“ bzw. „durchwandern“.
Für den Neubaurundgang kann man nachprüfen, dass der zugehörige Graph ein geschlossener Eulerkreis ist, d.h. dass alle Ecken (Räume und die Außenfläche) eine gerade Anzahl Kanten, d.h. Türen haben. Damit kann der stolze Hausbauer seine Präsentation planen.

Es gibt eine Gruppe von Figuren, bei denen es interessant ist, ob sie sich mit einem Zug durchgehend zeichnen oder mit einem Faden zwischen Nägeln spannen lassen oder nicht d.h. ob es sich um geschlossene Eulerkreise handelt oder nicht. Bekannt und beliebt ist hier das Pentagramm, wohl gleich nach dem Nikolauseigenheim.
Es handelt sich um regelmäßige Vielecke, bei denen jede Ecke mit jeder anderen Ecke durch eine Kante verbunden wird. Beim Quadrat gelingt es schon einmal nicht. Vergisst man eine Diagonale, dann erhält man nur einen offenen Eulerkreis. Aber das Pentagramm im regelmäßigen Pentagon ist ein geschlossener Eulerkreis. Ebenso ist das Siebeneck ein solcher. In der Mathothek gibt es eine weitere Anzahl solcher Objekte als Herausforderung:
Neben diesen „Sternen“ gibt es in der Mathothek noch einige solcher Fadenbilder. Dabei zeigt sich das befriedigende Gefühl, nun mit dem Wissen über Eulerkreise und ohne Herumprobieren und Scheitern – vielleicht aus eigenem Unvermögen – eine sichere Antwort auf solche Fragen geben zu können.
Es gibt in der Mathothek noch weitere solcher Faden-Bilder:

Was passiert, wenn Du dem „Haus des Nikolaus“ noch zwei Kanten von den beiden unteren Ecken zur obersten Ecke (Dachspitze) hinzufügst?
… und noch was:







