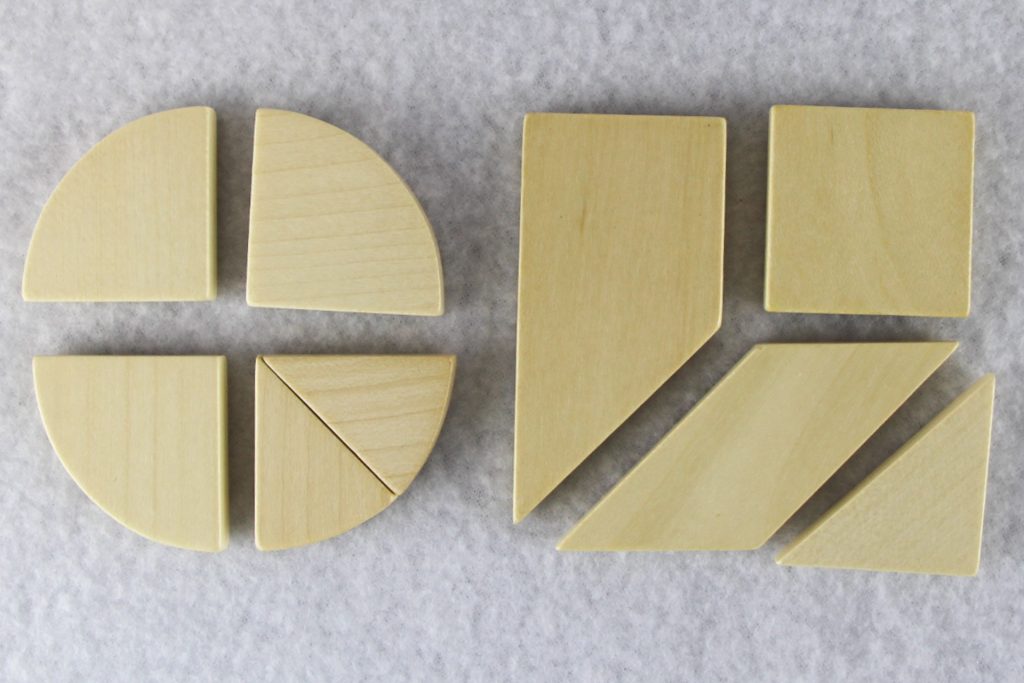Mancher Mensch leidet an einem “gebrochenen Herzen”. Ist die Ursache für dieses Leiden nicht zu beseitigen, so kann auch Ablenkung die Not lindern, vorzüglich mit Mathematik und logischen Herausforderungen. Beides steckt oft in hübschen Puzzles, z.B. in den beiden fast gleichen Legespielen, Gebrochenes Herz I und II:
Die Teile von Herz-Puzzle I setzen sich aus vier Viertelkreisen, zwei Quadraten, einem Parallelogramm und zwei Dreiecken, die beide rechtwinklig und gleichschenklig sind, zusammen. Bei II ist einer der vier Viertelkreise durch zwei Achtelkreise und ein Dreieck mit einem Quadrat durch ein entsprechendes Trapez ersetzt worden. Beide Male ließen sich die fünf bzw. vier Polygone (eckigen Teile) in acht kongruente Dreiecke zerlegen. In beiden Fällen besteht die Aufgabe darin, aus den jeweiligen Teilen ein Herz zu legen. Lösung am Ende des Artikels.
Mit den gleichen geometrischen Flächenformen, wie das Gebrochene Herz, Legespiel II enthält, lässt sich auch ein Quadrat mit an zwei Seiten angehängten Halbkreisen legen:
Auch diese Lösung erfolgt gegebenenfalls als “Erlösung” aus vergeblichem Bemühen ganz am Ende.
Aus den türkisen Teilen, bei denen viele nicht so bekannte und benannte geometrische Formen besitzen, lässt sich eine eiförmige Form mit dickem und spitzem Ende legen:
Es könnte sich natürlich auch um das Ei des Kolumbus handeln, das man jedenfalls mit den geformten steinernen Legesteinen des Anker-Puzzles in 2D-Format bauen kann:
Es gibt in der Mathothek noch weitere solche nostalgisch anmutende Stein-Puzzles. Die beiden folgenden geometrischen Legespiele sind sehr einfach zu lösen, wenn man weiß, dass ein Kreis und eine Raute gesucht werden.
Alle Neune: Die Legesteine bestehen aus sieben verschiedenen Dreiecken und zwei gleichen Trapezen, aus denen sich – ähnlich wie beim Tangram – verschiedene Figuren legen kann.
Auch Der Zornbrecher ist ein solches Steinpuzzle. Es besteht aus einem in drei Dreiecke und vier Fünfecke zerlegten regelmäßigen Achteck:
Auch aus der Zerlegung eines regelmäßigen Achtecks stammen die sieben Legesteine eines weiteren blauen Steinpuzzles, das dem klassischen Tangram in vieler Hinsicht ähnlich ist. Dieses Legespiel besteht auch aus sieben Bausteinen, die besondere Vielecke sind und zusammen zwar kein Quadrat, sondern ein regelmäßiges Achteck ergeben.
Ehe jetzt die Lösungen gelüftet werden, folgt noch ein völlig aus der Reihe tanzendes und eher biologisch-organisch wirkendes Legespiel:
Das “Unwiderstehlich Puzzle”:
… und hier die – hoffentlich auch selbst gefundenen – Lösungen der Reihe nach:
Die gebrochenen Herzen:
Eiförmige Form:
Ei des Columbus:
Blauer Kreis und rote Raute:
Mit Ausnahme des letzten Puzzles sind alle bisherigen gezeigten Beispiele für Legespiele aus einer größeren, meist mathematischen Form in kleinere geometrische Legeteile geschnitten worden. Auch das bekannteste so konstruierte Legespiel, der Klassiker auf diesem Gebiet, das Tangram ist in der Mathothek mehrfach vorhanden und findet sich in einem gesondertem Artikel dargestellt.
Beim Tangram gibt es genau sieben Grundfiguren, ein Quadrat, ein Parallelogramm, zwei kleine, zwei große, kongruente gleichschenklige Dreiecke und ein mittleres gleichschenkliges Dreieck. Das Verhältnis der Dreiecke beträgt 1:2 und 1:4, d.h. die zwei kleineren ergeben das mittlere Dreieck, das große Dreieck erhält man aus zwei mittleren oder acht kleinen Dreiecken. Alle sieben Grundbausteine zusammen ergeben ein Quadrat, das sich aus 64 kleinen Dreiecken ergibt.
Tangram ist der westliche Name für ein sehr altes Lege- und Geduldsspiel, das vermutlich bereits zwischen dem achten und dem vierten Jahrhundert vor Christus in China entstand.
In der Mathothek gibt es ein weiteres “Tangram”. Das Ägyptische Tangram besitzt nur zwei Formen, ein rechtwinkliges Trapez und ein rechtwinkliges Dreieck, die jeweils zusammen ein Quadrat ergeben.
Mit diesen fünf Trapezen und fünf Dreiecken lassen sich mithilfe von Vorbildern oder der eigenen Phantasie viele Figuren legen, die trotz ihrer “Eckigkeit” an reale Dinge erinnern. Hier ein Beispiel:
Es stammt aus dem anregenden Buch: Geduldspiele der Welt von Jack Botermans und Jerry Slocum.
Auch die Anregung zum Nachbau des “Ägyptischen Tangrams” kam aus diesem Buch.
Das ebenfalls in der Mathothek nachempfundene “Tangram” und nach dem griechischen Mathematiker Archimedes benannte, LOCULUS ARCHIMEDUS oder STOMACHION DES ARCHIMEDES, besteht aus 14 Legeteilen, und zwar aus elf Dreiecken, zwei Vierecken und einem Fünfeck , die zusammen ohne Überlappung oder Lücken ein Quadrat ergeben.
Dieses Quadrat wieder zusammenzufügen, ist bereits eine herausfordernde Aufgabe. Aber auch hier gibt es Vorlagen zum Nachlegen vieler klassischer Figuren. Aber auch die eigene Phantasie kann wunderbare neue Figuren hervorbringen.
Während dieses archimedische Stomachion eine ziemlich differenzierte Zerlegung eines Quadrates ist, bei dem recht verschiedene Formen, vor allem Dreiecke entstehen, ist die nächste Quadratzerlegung in vier kongruente Trapeze sehr einfach, aber für Anfänger nicht nutzlos:
Aber Legeaufgaben mit nur Teilen. die alle dieselbe Form haben, kann sehr wenig herausfordernd sein, aber uns im Alltag oft begegnen.
Aber sobald man die Elemente mischt, also Parkette entwirft, entstehen geometrische Herausforderungen:
Zu solchen Parkettierungen gibt es in der Mathothek sehr viele und die geometrischen Erfahrungen bereichernde Experimente auch in der Form von Legespielen.
Aber auch Legespiele mit – genau genommen – nur einer Grundform können zu interessanten Herausforderungen werden, wenn aus diesen kleinsten Elemente größere Bauteile zusammengesetzt werden. Das wird in der Mathothek nicht nur am Beispiel der Hexominos erlebbar. Dabei sind Hexominos alle Formen, die durch das Zusammenkleben von sechs kongruenten, gleichseitigen Dreiecken entstehen.
Auch die konkaven Vierecke und ihre möglichen Zerlegungen, die ihre Flächenberechnungen und Formeln dafür erfahrbar machen, bietet die Mathothek in Form von “Legespielen” an, z.B.
Die Freude am freien und kreativen Spiel, das offene und gezielte Experimentieren und die analytische und logische Durchdringung sind die Wege zum Verstehen der Welt.