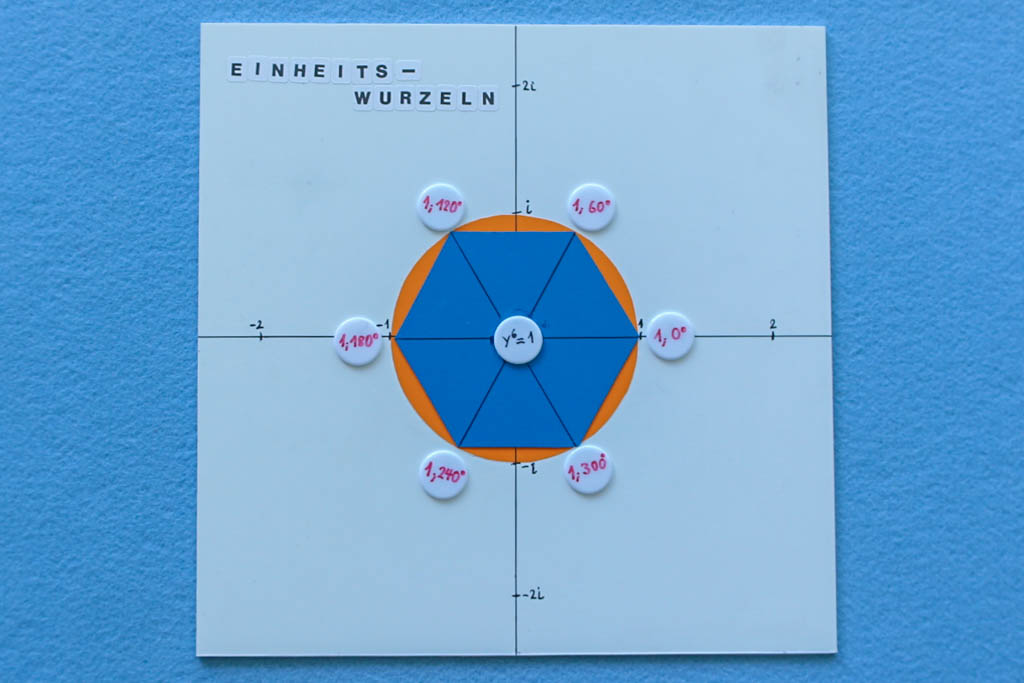
Dieses robuste Exponat wird bei seiner Benutzung meistens im Flur aufgebaut, und zwar nicht weil es unangenehm riecht oder riesengroß ist, sondern ziemlich viel Lärm machen kann, wenn es nicht gelingt. Allerdings kann es dadurch auch beim Schulfest oder am…
Was passiert, wenn ein Frauchen, ihr Hund, eine Katze und eine Maus ganz zufällig so platziert sind, dass diese vier die vier Ecken eines Quadrates bilden, die Frau auf den Hund zuläuft, der Hund dann nach der Katze rennt, die…
Bei allen Zahlenbereichen, die aus den “gottgegebenen” natürlichen Zahlen bis zu den reellen Zahlen durch Erweiterungen konstruiert wurden, geschah dies so, dass neue Anwendungen und Lösungen für weitere Probleme geschaffen wurden, dass aber diese Erweiterungen so erfolgten, dass das Bisherige…
In diesem Artikel werden vier klassische Fraktale vorgestellt, ihre Konstruktion gezeigt, besondere Grenzwerte untersucht und versucht, ihre “gebrochene” Dimensionen zu erklären. Als erstes Beispiel betrachten wir “Cantors Staub”: Dieses Objekt veranschaulicht die ersten fünf Schritte zur Konstruktion des “Cantor-Staub” genannten…
Dieses farbig und flächenhaft gestaltete Bild in der Mathothek ist eine besonders ansprechende Darstellung der Koch’schen Schneeflockenkurve. Wie der Name schon sagt, ist das dahinterstehende Gebilde nur eindimensional. Es handelt sich bei der Schneeflockenkurve eigentlich nur um den Rand. Ursprünglich…
Dieses Bild des “Apfelmännchen in schwarz-weiß” lässt noch nichts von der Faszination dieser legendären fraktalen Figur erkennen. Aber dafür wird die Bezeichnung besonders einleuchtend. Deutlich erkennbar ist auch die Selbstähnlichkeit der Figur: Regelmäßig tauchen neue “Apfelmännchen” in entsprechenden Verkleinerungen auf.…
In der Mathothek gibt es sehr viele Exponate, wovon die meisten interaktiv zu nutzen sind, mit denen man verstehend erfahren kann, wie die Menschen im Laufe der Geschichte Zahlen und das Rechnen mit ihnen bis zum heutigen Rechner entwickelt haben.…
Im Zusammenhang mit dem Binärsystem gibt es in der Mathothek verschieden lange Teile eines runden Holzstabes, mit denen sich beispielsweise Schüler im Binärsystem messen können. Das ist deswegen möglich, weil die Stäbe bestimmte Längen besitzen. Die Längen – in cm…
Das cavalierische Prinzip ist ein sehr hilfreiches Mittel, um bei einer Vielzahl von Körpern das Volumen (=Rauminhalt) zu bestimmen. Wenn wir uns diesen Flakon anschauen, so scheint die Berechnung des Volumens eines solchen geschwungenen Körpers keine einfache Sache zu sein.…
Das Unendliche und seine “Zähmung” ist der Mathematik ureigenstes Thema. Besonders im 19. und in der ersten Hälfte des 20. Jahrhunderts wurden die Begriffe des “unendlich Großen und unendlich Kleinen” grundlegend definiert und die Analysis auf ein tragfähiges Fundament…