Eine natürliche Zahl heißt Primzahl, wenn sie genau zwei Teiler hat. Oft sagt man auch, Primzahlen sind natürliche Zahlen, die nur durch sich und 1 teilbar sind. In diesem Fall muss allerdings dazugesagt werden, dass 1 keine Primzahl ist. Auf dem unten abgebildeten Zahlenstrahl sind die ersten Primzahlen mit einem roten Ring versehen:
Ein Beispiel für ein recht einfach zu beweisendes Muster in der Menge der Primzahlen ist die Eigenschaft, dass das Quadrat jeder Primzahl, die größer als 3 ist, minus 1 ein Vielfaches von 24 ist: 52-1=24, 72-1=48, 112-1=120, 132-1=138, 172-1=288, … Jetzt kann man ewig so weitermachen und wird nie zu einem Ende kommen. Um einzusehen, dass das so ist, müssen wir die Wahrheit der Behauptung, dass das Quadrat jeder Primzahl um 1 vermindert ein ganzes Vielfaches von 24 ist, logisch beweisen. Dafür formalisieren wir die Behauptung ein wenig:
Für alle Primzahlen n≥5 gibt es eine natürliche Zahl k, sodass gilt: n2-1=k⋅24.
Beweis: Für jede natürliche Zahl n gilt n2-1=(n-1)⋅(n+1). Dann muss von den drei Zahlen n-1, n und n+1 mindestens eine gerade Zahl sein. Da in unserem Fall n eine Primzahl ≥5 ist, müssen ihr Vorgänger n-1 und Nachfolger n+1 beide gerade Zahlen sein. Somit ist das Produkt der beiden Zahlen (n-1)⋅(n+1) durch 2 und 4 und damit durch 8 teilbar.
Eine der drei Zahlen, n-1, n oder n+1 muss auch durch 3 teilbar sein. Wiederum kann das nicht n sein, weil n>3 ist und dann keine Primzahl sein könnte. So ist auch 3 ein Teiler von (n-1)⋅(n+1).
Da 8 und 3 teilerfremd sind, d.h. sie besitzen nur die 1 als gemeinsamen Teiler, muss (n-1)⋅(n+1) auch durch 3⋅8=24 teilbar sein. Da (n-1)⋅(n-1)=n2-1 ist, gibt es eine natürliche Zahl k mit n2-1=k⋅24
w.z.b.w. [Was zu beweisen war.]
Nun wären die Primzahlen nie zu diesen besonders geliebten Objekten in der Mathematik geworden, läge ihnen ein so einfaches „Auffindungsgesetz“ zugrunde, das man durch die erhielte, die Umkehrung der obigen Behauptung erhielte. Leider gilt die Umkehrbehauptung:
Jede natürliche Zahl n ist eine Primzahl, wenn sich eine natürliche Zahl k finden lässt, sodass n2-1=k⋅24 gilt.
Ein einziges Gegenbeispiel widerlegt eine solche „Für alle…“-Behauptung. Wenn Du hier systematisch die Folge der natürlichen Zahlen überprüfst, stößt Du mit n=25 auf das erste Gegenbeispiel:
252-1=625-1=624 und 26⋅24=624, aber 25 ist leider keine Primzahl!
Dass es unendlich viele Primzahlen gibt und damit keine größte Primzahl geben kann, ist schon seit der Antike bekannt. In der Mathothek gibt ein fiktives Gespräch einer realen Schülerin Lisa und dem antiken Mathematiker Euklid. In diesem Gespräch wird Euklids Beweis dafür, dass es keine größte Primzahl geben kann so vermittelt, dass es auch für jüngere Schüler gut verständlich wird. Dieses Objekt der Mathothek entstand anlässlich einer missverständlichen Schlagzeile in einer Wiesbadener Zeitung.
Tatsächlich ist eine heftige Jagd auf immer mehr und immer größere Primzahlen zu beobachten. Der Bedarf an solchen großen Primzahlen ist in der Informatikbranche zur Verschlüsselung recht groß. Auch die Computerindustrie arbeitet werbewirksam mit immer größeren Primzahlen auf, um Leistungsfähigkeit und Zuverlässigkeit ihrer Produkte zu demonstrieren.
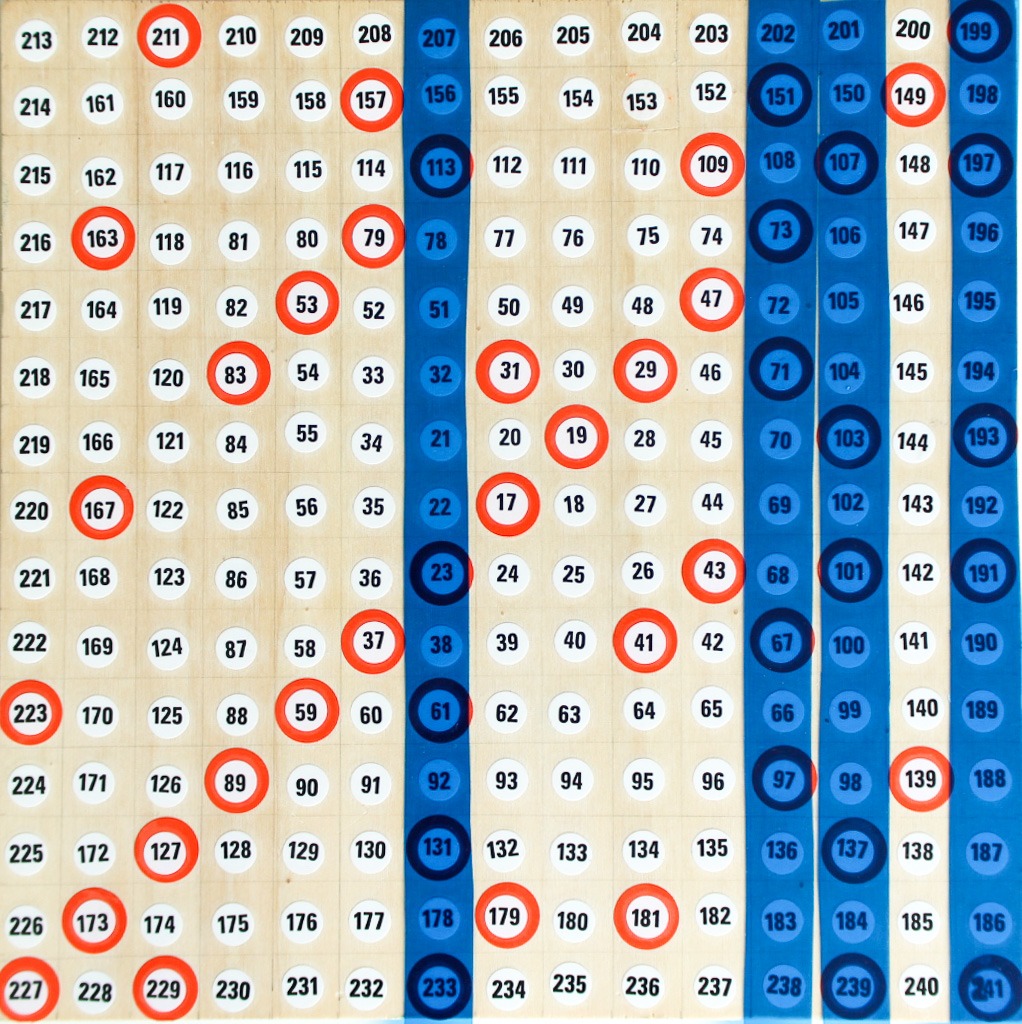
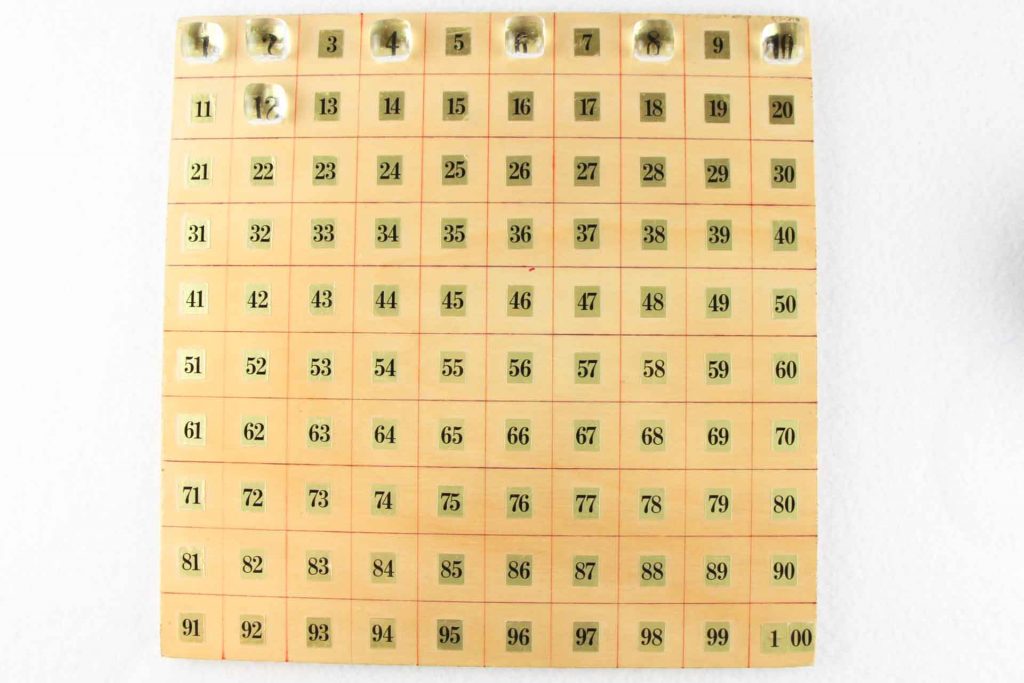
Das oben abgebildete Experiment der Mathothek zeigt einen weiteren Versuch, durch verschiedene Anordnungen der natürlichen Zahlen interessante Verteilungsmuster der Primzahlen sichtbar werden zu lassen. Besonders interessant ist die Ulam-Spirale oder Primzahl-Spirale. Dazu gibt es auch ein interaktives Exponat in der Mathothek. Es besteht aus einem Quadrat mit in Reihen und Spalten eingetragenen natürlichen Zahlen, die in eckigen Spiralen um den Mittelpunkt des Quadrates der Größe nach angeordnet sind. Dabei beginnt die Spirale mit 17 und geht bis 241. Man könnte diese Ulam-Spirale auch mit jeder anderen natürlichen Zahl beginnen lassen, selbstverständlich auch mit 1. In jedem Fall sind ähnliche Muster zu beobachten: Die Primzahlen auf unserer Tafel sind mit einem runden Ring gekennzeichnet.
Mit den transparenten blauen und grünen Streifen lässt sich gut zeigen, dass die Primzahlen in dieser Tabelle mehrheitlich auf diagonalen Linien, aber auch auf waagrechten oder senkrechten Linien liegen.
1963 hat der polnische Mathematiker Stanislaw Marcin Ulam aus Langeweile, die er während eines wissenschaftlichen Vortrags empfand, Zahlenreihen auf ein Papier gekritzelt. Mit der 1 in der Mitte beginnend, trug er die weiteren natürlichen Zahlen spiralförmig in immer größer werdenden Quadraten ein und markierte anschließend die Primzahlen. Dabei entdeckte er, dass die Primzahlen in großer Anzahl auf diagonalen Linien lagen. In unserem Experiment lassen sich diese Linien durch transparente blaue und grüne Streifen sichtbar machen.
Links sind mit grünen Streifen alle von l.u. nach r.o. verlaufenden Diagonalen markiert, auf denen sich drei und mehr Primzahlen befinden. Natürlich kann man die von l.o. nach r.u. verlaufenden Diagonalen untersuchen. Aber auch eine gehäuftes Auftreten von Primzahlen in senkrechten Spalten und in waagrechten Zeilen ist zu beobachten. Unten sind alle senkrechten Spalten mit mehr als drei Primzahlen blau markiert:
Inzwischen wurden sehr viele solcher Ulam-Spiralen mit sehr großen Zahlen (z.B. über eine Million) und solche die nicht mit 1 beginnen, sondern mit viel größeren Startzahlen als 1 untersucht. Es scheint so zu sein, als würden die Diagonallinien in allen solchen Mustern eine bevorzugte Rolle spielen. Trotz einiger Teilerklärungen kann das Muster der Ulam-Spirale bis heute nicht vollständig erklärt werden.
Lehre: .nenrienilpizsid llenhcs uz nednutssthcirretnu negiliewgnal ni rednik ednleztirk etllos naM
Dass in der Mathematik die Primzahlen als Bausteine der natürlichen Zahlen eine so wichtige Rolle spielen, dass so viele Eigenschaften gefunden und bewiesen wurden, dass aber immer noch ganz grundsätzliche Geheimnisse nicht gelüftet werden konnten, das macht die Beschäftigung mit der Welt der Primzahlen weiter spannend. Wird je die menschliche Intelligenz und Kreativität zu den Antworten auf die grundlegenden Fragen der so vielschichtigen Elementen vordringen?
Drei solche Fragen der Mathematiker, auf deren Beantwortung man wartet:
Gibt es unendlich viele Primzahlzwillinge? Als Primzahlzwilling bezeichnet man zwei Primzahlen, die nur durch eine Nicht-Primzahl getrennt sind, z.B. 3 und 5, 5 und 7, 11 und 13 usw.
Gibt es zwischen zwei Quadratzahlen immer mindestens eine Primzahl? Zum Beispiel liegen zwischen 9 und 16 die Primzahlen 11 und 13, zwischen 16 und 25 die Primzahlen 17, 19 und 23.
Gibt es zu jeder natürlichen Zahl >2 zwei Primzahlen, die von dieser Zahl gleich weit entfernt sind? Zum Beispiel sind die Primzahlen 11 und 13 gleich weit von 12, die Primzahlen 17 und 29 sind gleich weit von 23 entfernt usw.
Zu keiner dieser drei Fragen hat bisher jemand ein Gegenbeispiel gefunden, aber auch keinen Beweis erbracht. Bei den beiden ersten Fragen sind aber sehr viele – Milliarden – Zahlen überprüft worden, ohne Widerspruch. Zu den beiden letzten Fragen gibt es jeweils eine Vermutung.
Zu der dritten Frage – Goldbach’sche Vermutung – gibt es in der Mathothek ein gut erklärendes Exponat:
Man sieht an diesen wenigen Beispielen auch eine große Bandbreite: Es gibt zu den Primzahlen einfach zu verstehende und formulierbare Aussagen, die auch einfach zu beweisen sind, aber auch solche einfach zu formulierenden Vermutungen, die bis heute noch von keinem Mathematiker bewiesen worden sind.
Zu dem faszinierenden Thema der Primzahlen gibt es in der Mathothek noch weitere interessante Exponate: