Die drei „grauen Mäuse“ fallen in ihrer Bescheidenheit an der schmalen Seite der Fensterwand kaum auf. Die farbigen und viel auffälligeren Bilder und Objekte „um die Ecke“ beherrschen für den Besucher hier die Szene.
Dabei haben diese „drei Geschwister“ ausgesprochen schöne „Kurven“ und bieten die Möglichkeit, mit ihnen weitere Kurven – mathematischer Art – zu erzeugen. Dieses Set aus drei Kurvenlinealen stammt aus der dunkelsten Corona-Zeit, als die Menschen Zeit hatten, ihre reichlich angesammelten Schätze auszusortieren und gegebenenfalls mit dem Hinweis „zu verschenken“ oder „Zum Mitnehmen“ als Sperrmüll am Straßenrand zu entsorgen. Dieser „Sperrmüll“ war (ist auch noch) ein geeignetes Hilfsmittel, um gegebene Punkte einer Ebene mit einer geeigneten „glatten Kurve“ zu verbinden.
Zwei weitere Hilfen, um Kurven zu zeichnen, sind die beiden folgenden Objekte:
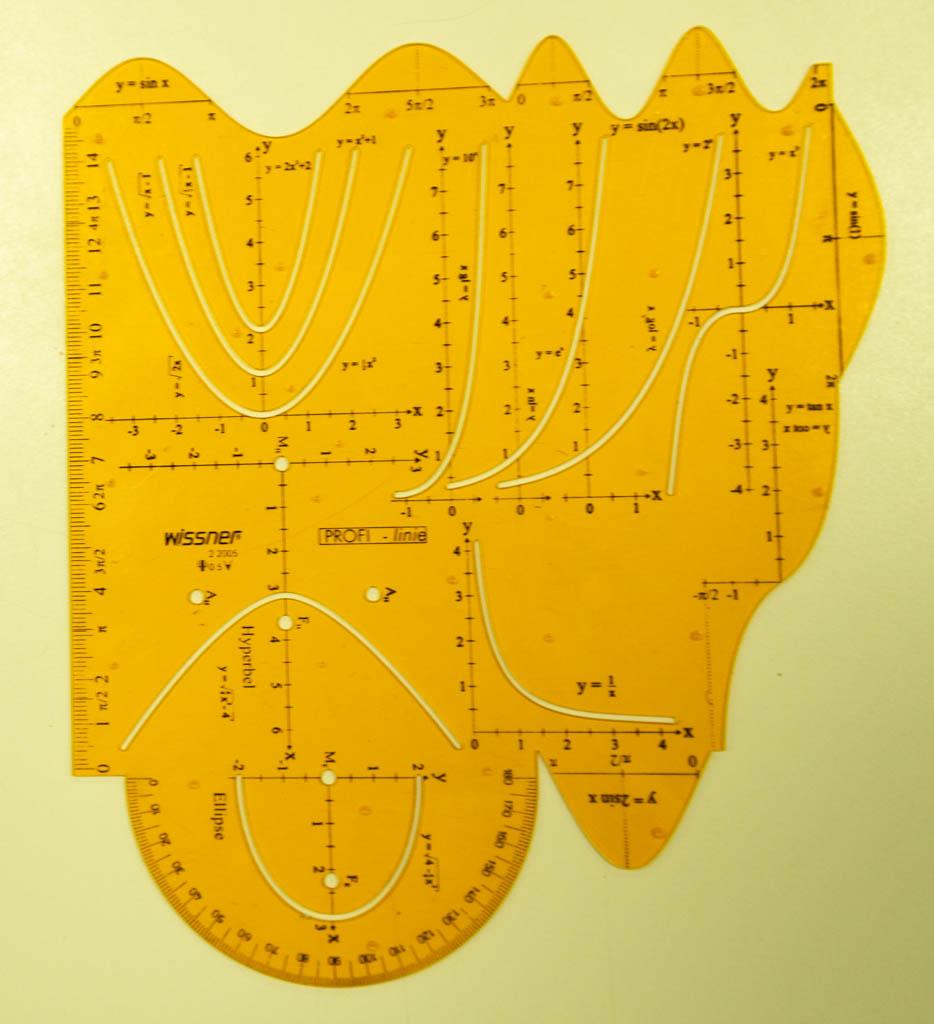
Diese Schablonen sind aus transzendentem Plastikmaterial, mit kurvenförmigen Öffnungen, durch die mit einem Zeichenstift die gewünschte oder geeignete Kurve durch gegebenen Punkte gezeichnet werden kann.
Eine besonders flexible Art von Kurven zu zeichnen, bietet ein solches biegsames Lineal aus Gummi oder Plastik:
Dieses Instrument ist ausgezeichnet geeignet, um Kurven zu bilden, die besonders „glatt“ sind, die keine Ecken oder Spitzen haben. In der Differenzial- und Integralrechnung erhält man solche Kurven ohne Knicke als Graphen von differenzierbaren Funktionen.
In jedem Punkt der Kurve existiert eine Tangente der Kurve. Im Beispiel veranschaulicht der schmale Holzstab die Tangente im Berührpunkt. Dieses Objekt in der Mathothek erlaubt eine erste, sehr anschauliche Vorstellung zu Grundgedanken der Analysis.
Heute übernehmen weitgehend Computerprogramme – ohne sinnliche Erfahrungen – die Aufgabe, gewünschte und geeignete Kurven zu zeichnen.
Wenig Platz beansprucht und wenig Aufmerksamkeit erregt eine kleine runde, in der Nähe des Fensters stehende Porzellanschale. Fallen aber im richtigen Winkel Sonnenstrahlen in das weiße Innere von ihr, so fasziniert die herzförmige Kurve, die durch die Reflexion des Sonnenlichts entsteht.
Es gibt in der Mathothek für die über Tausend Exponate viel zu wenig Raum, um ihnen immer den verdienten Platz einzuräumen. Deswegen wird in der Mathothek jeder noch so kleine Fläche genutzt, wie auch an den Beispielen in diesem Artikel zu erkennen ist. Ein weiteres solches Beispiel für ein hochinteressantes Objekt, bei dem Platz und experimenteller Effekt im krassen Widerspruch stehen, ist das zur elektromagnetischen Induktion: