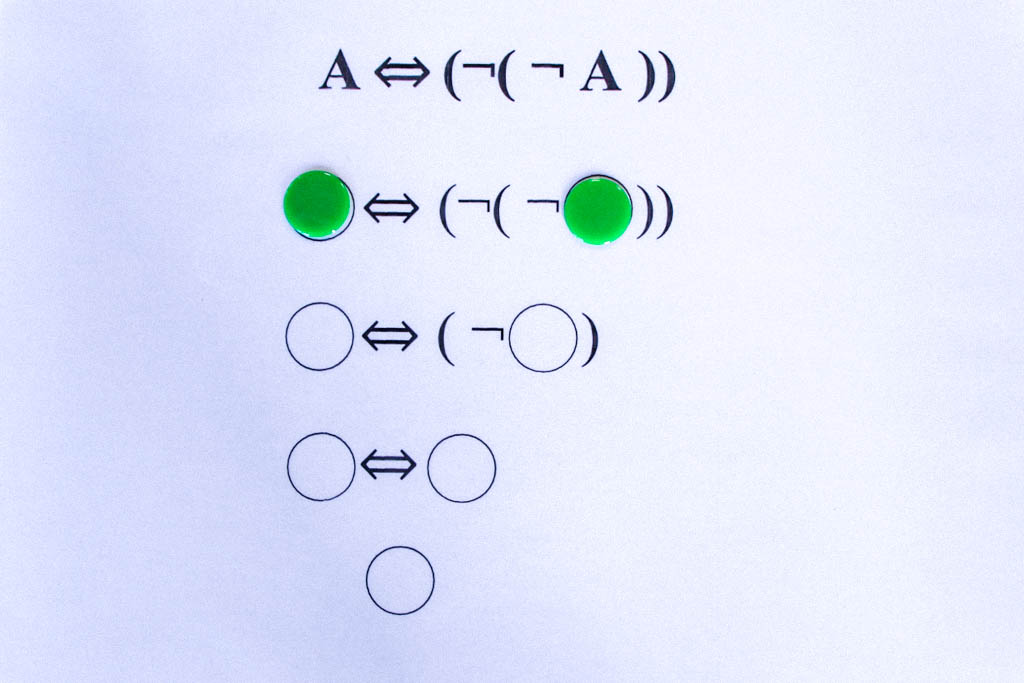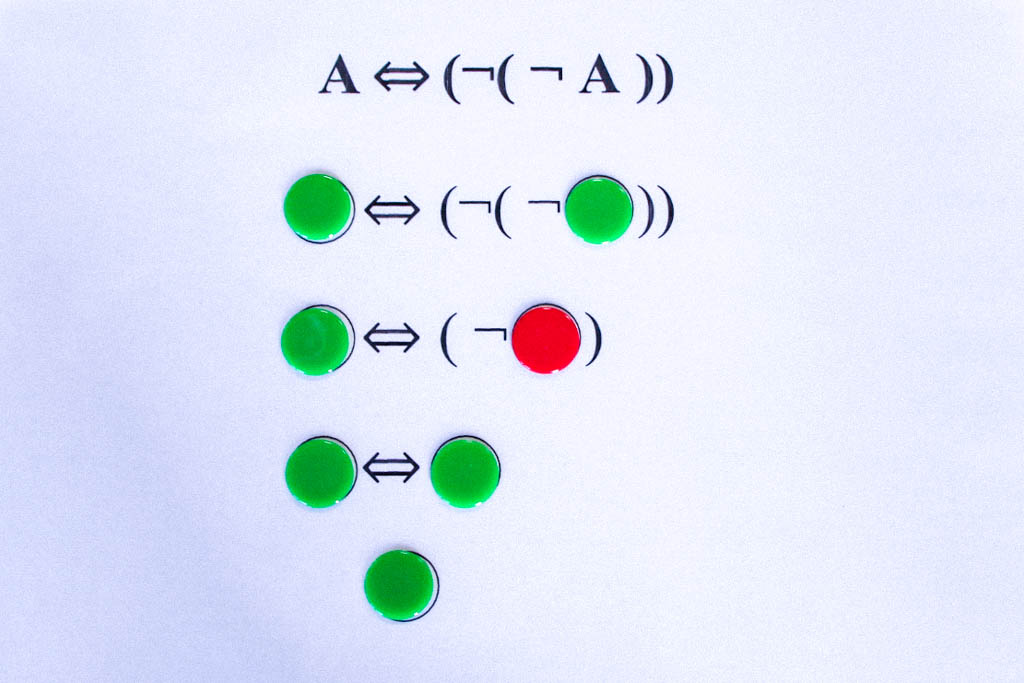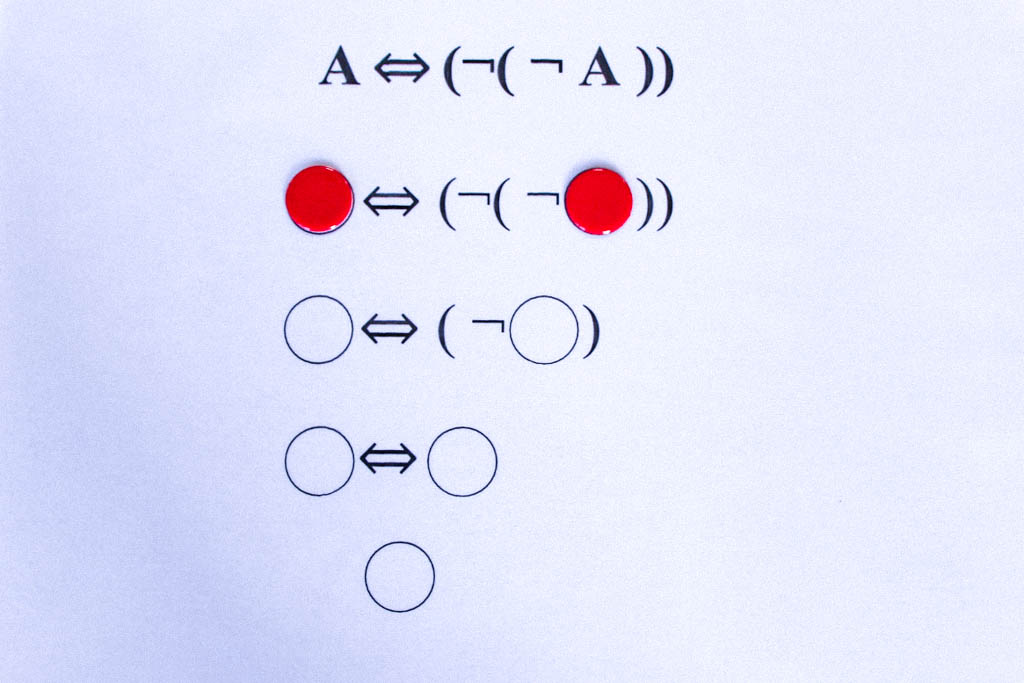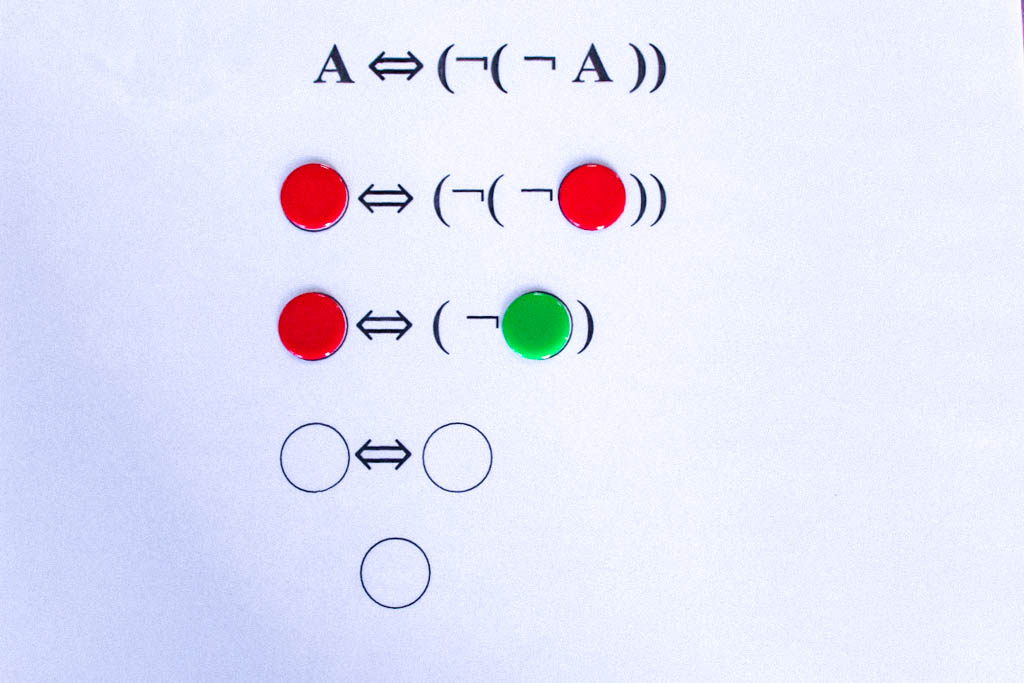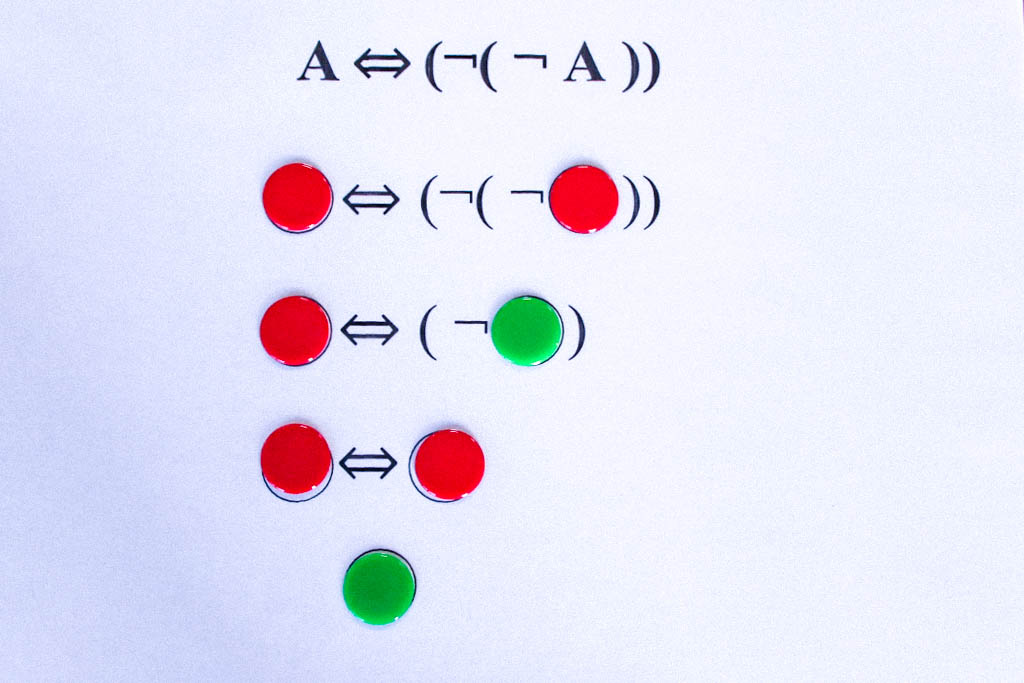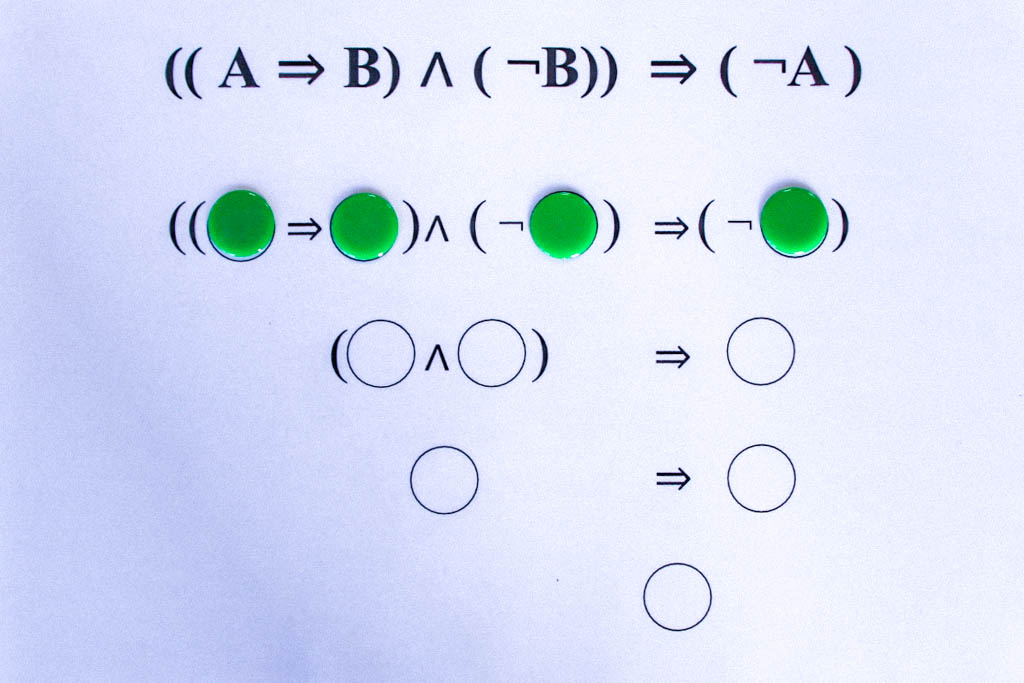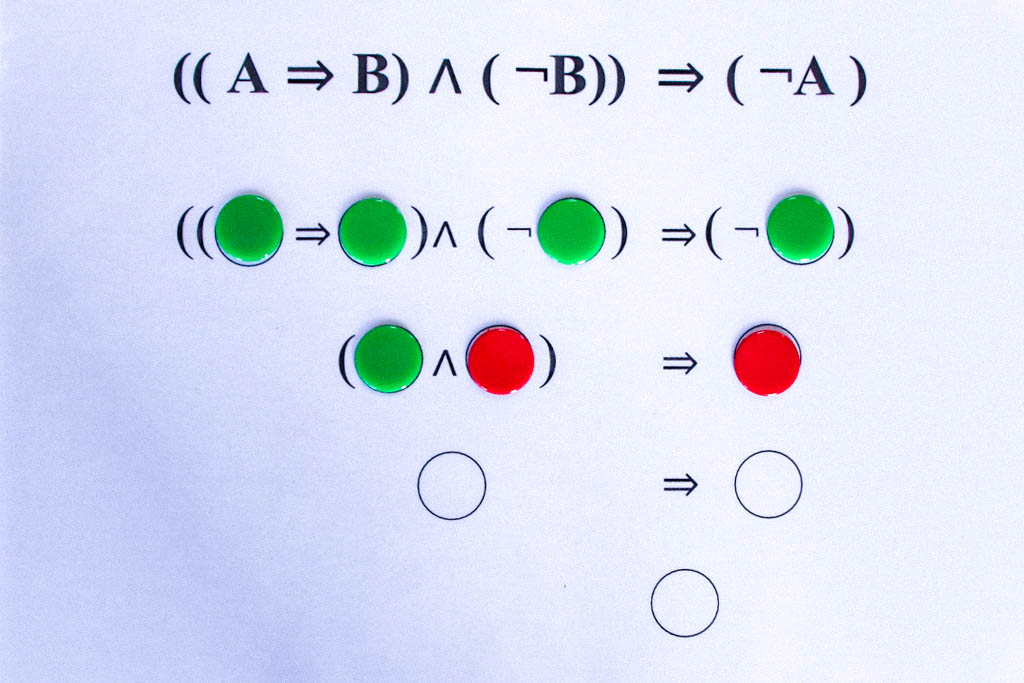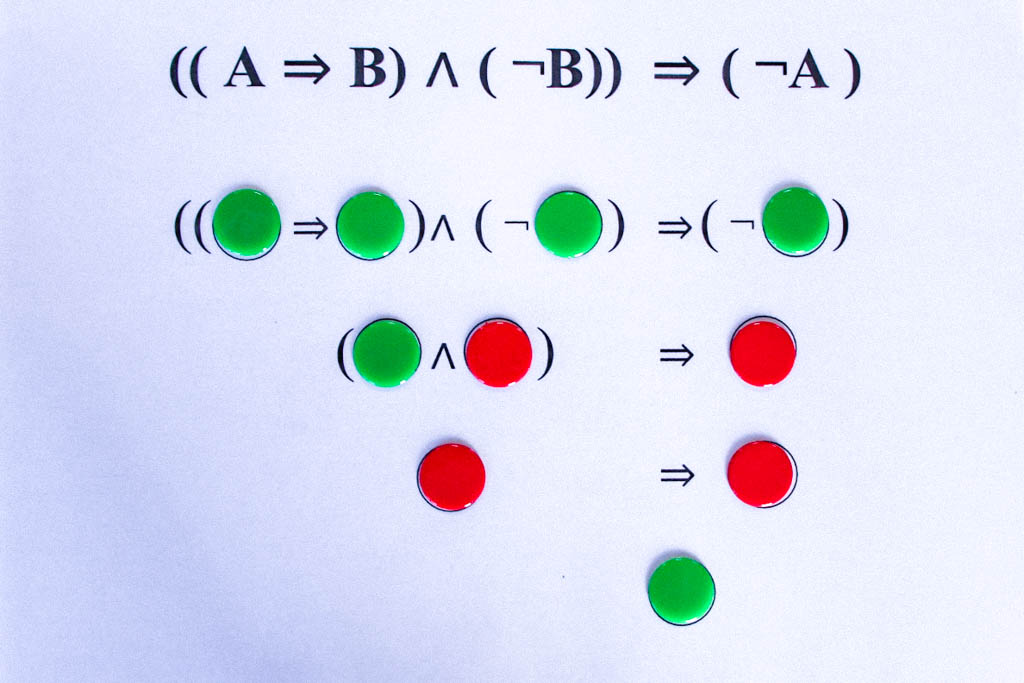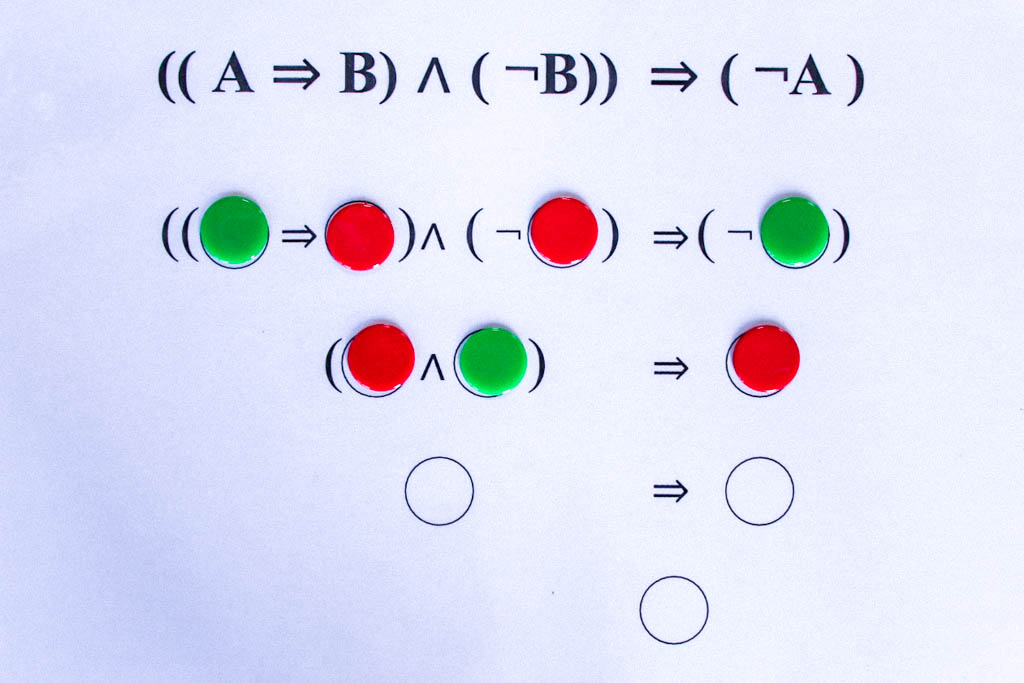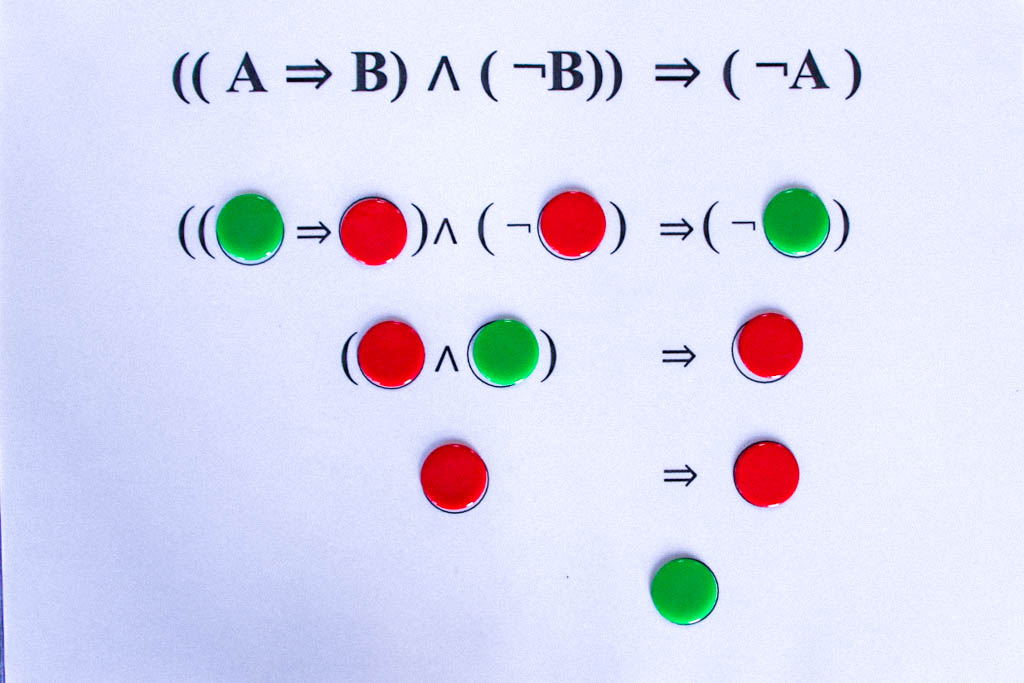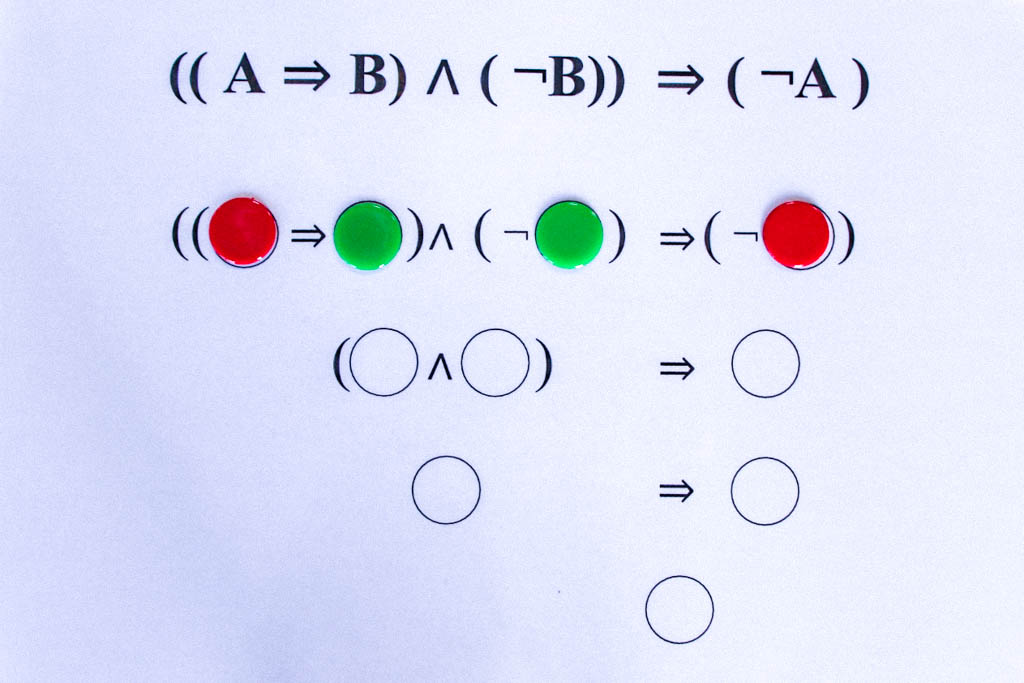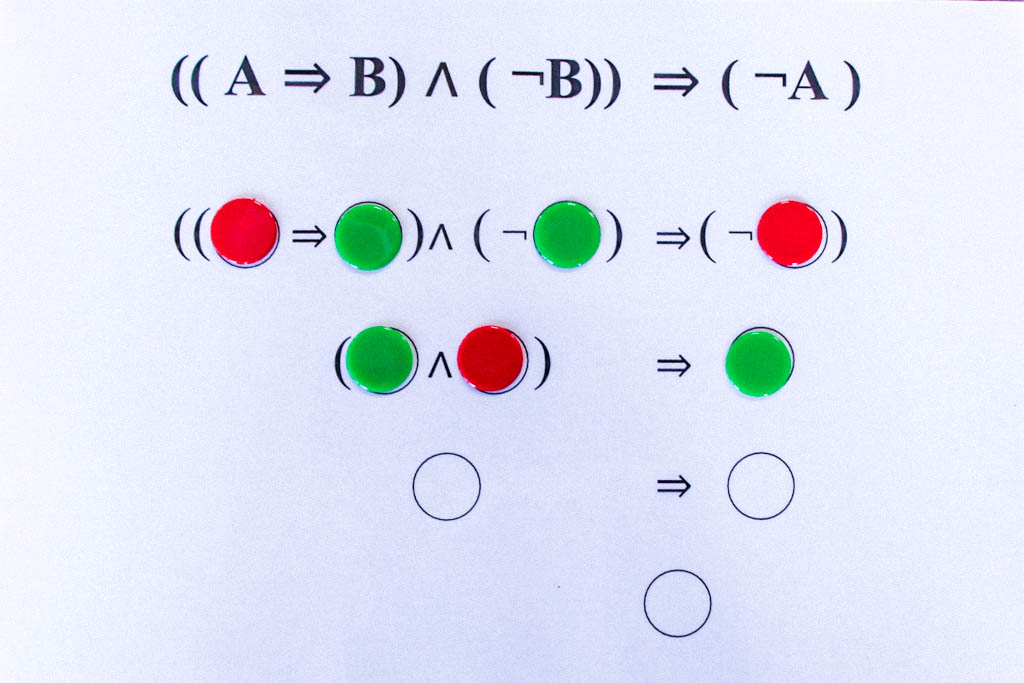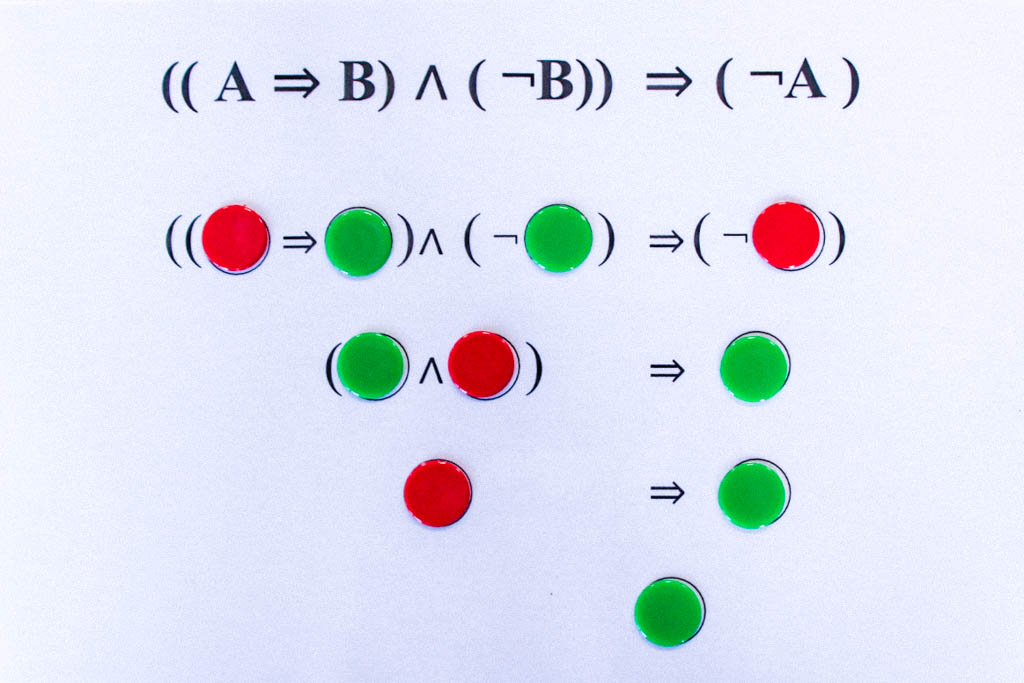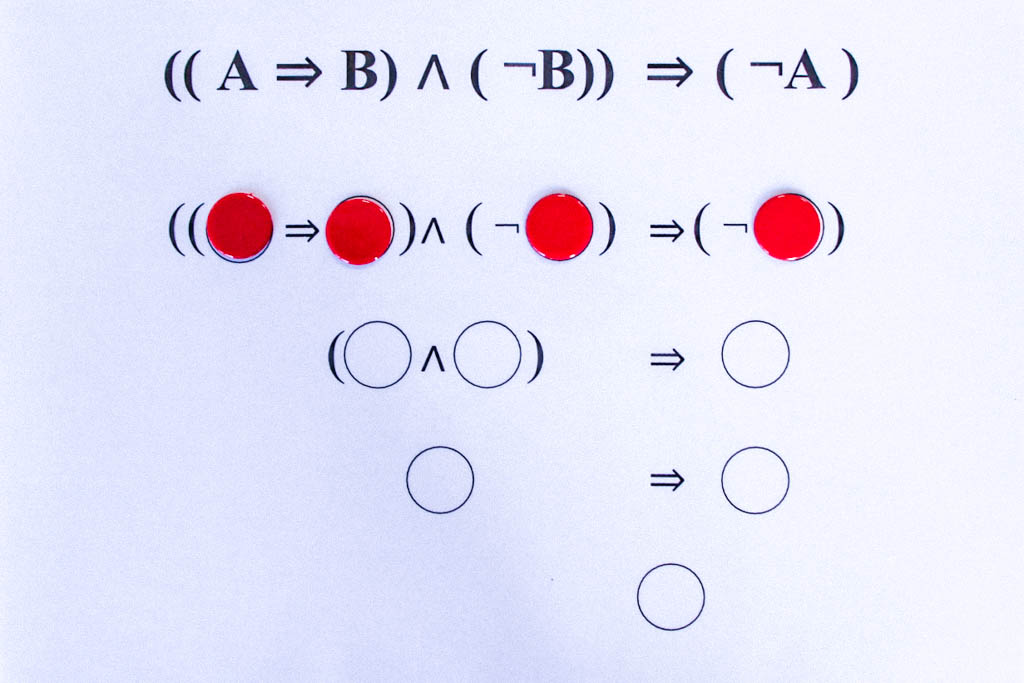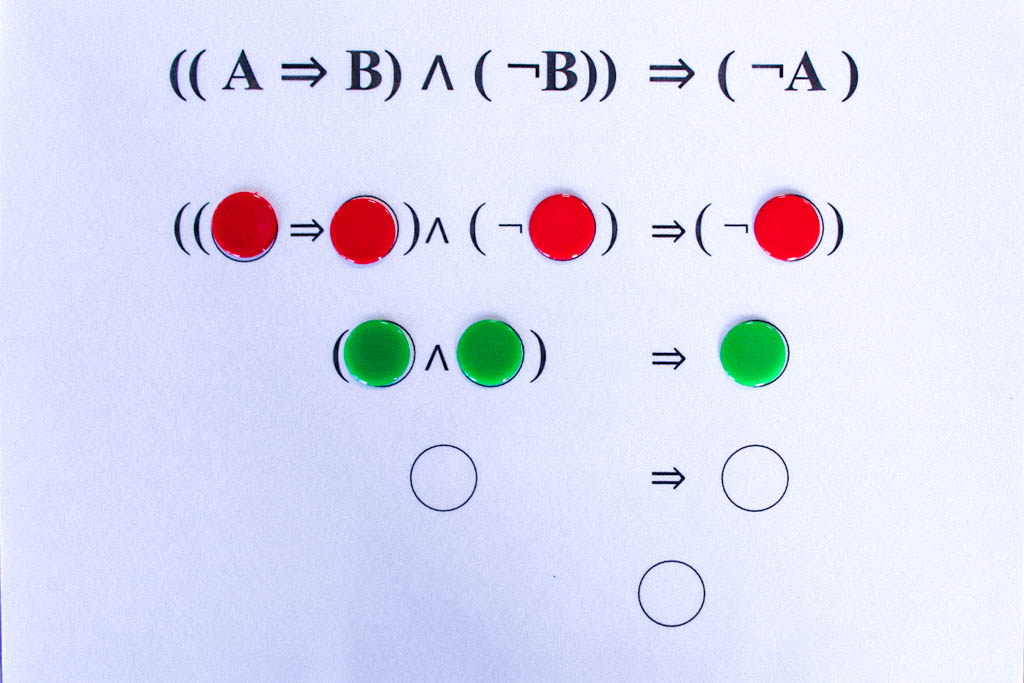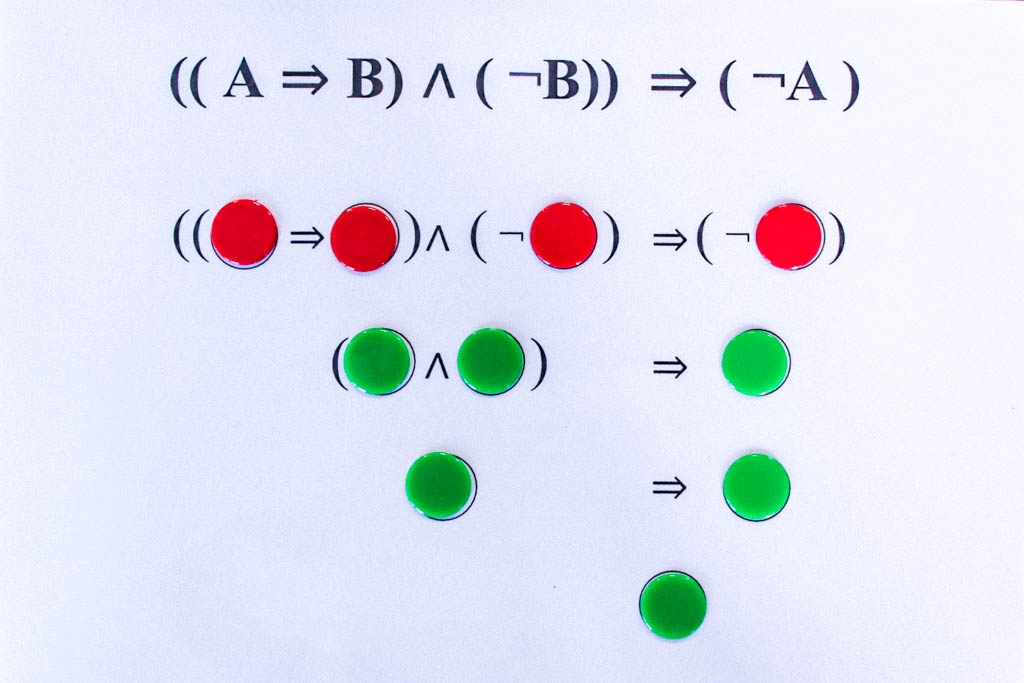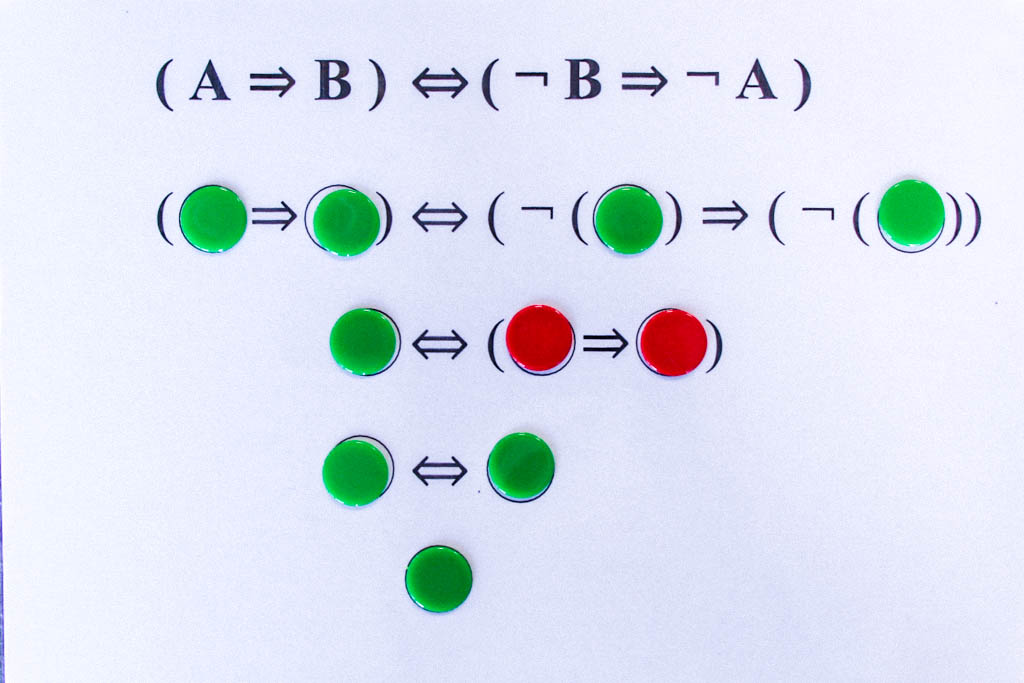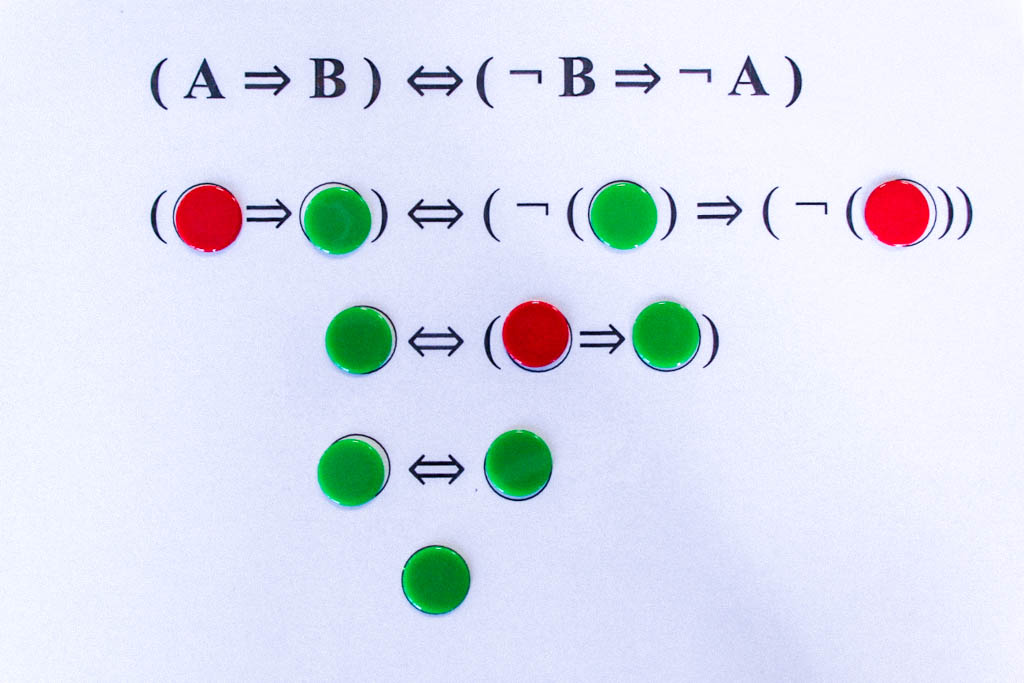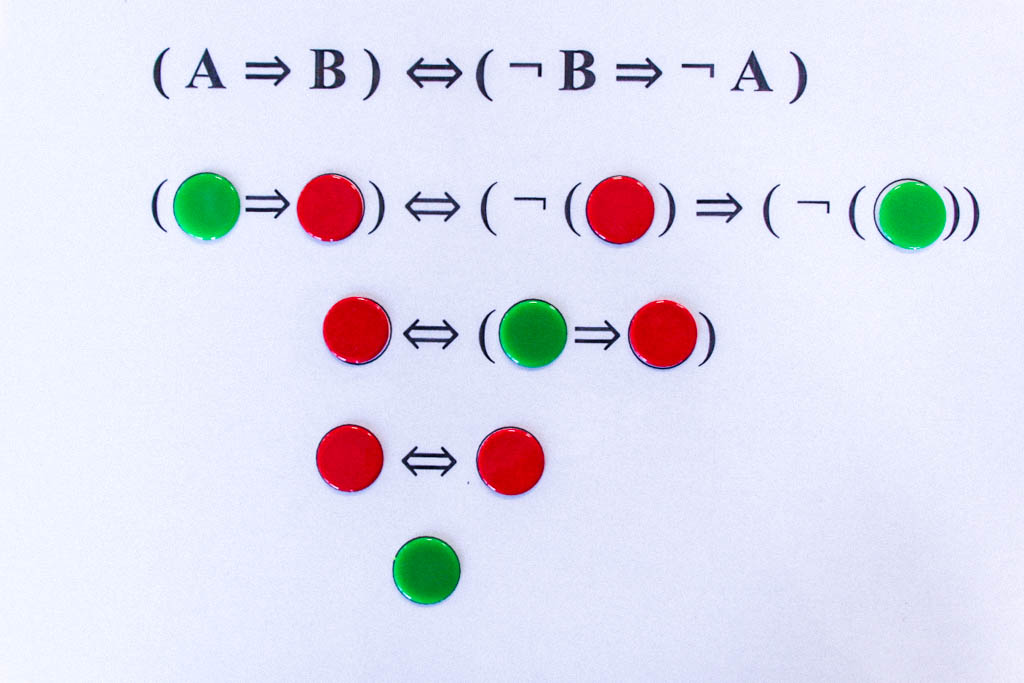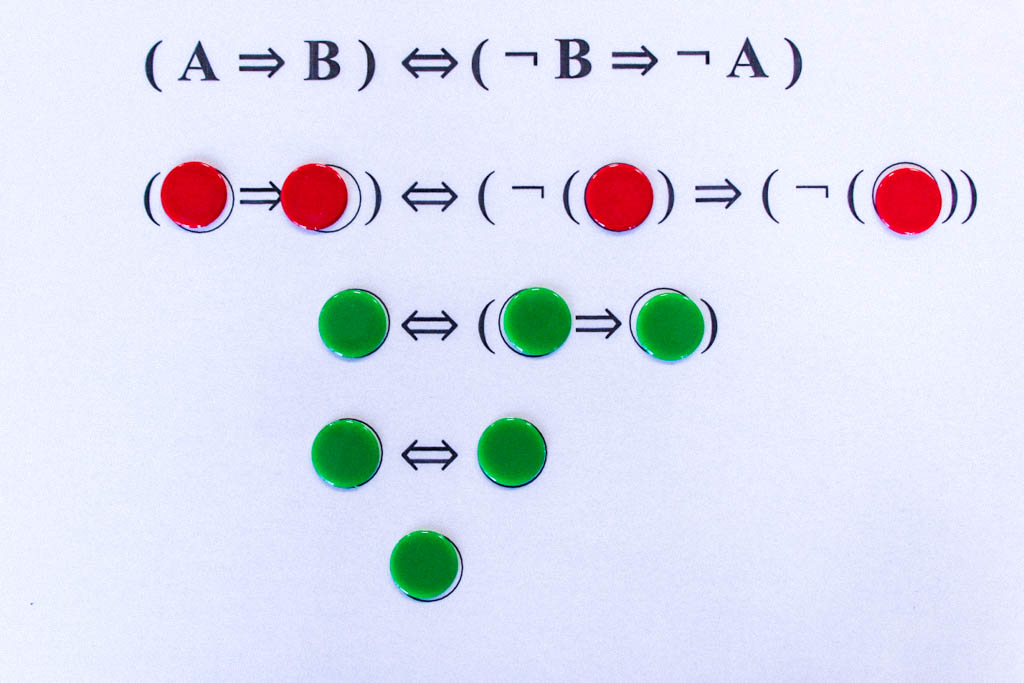Wie können wir helfen?
Wer kennt nicht die unwiderlegbare Wetterregel: “Kräht der Hahn auf dem Mist, ändert sich das Wetter oder es bleibt, wie es ist.” Eine Bauernregel, die überall und über alle Zeiten hinweg gültig ist. Hier bedarf es keiner langen Wetterbeobachtungen und ausführlicher Klimadaten. Diese Aussage ist wahr, und zwar nur aufgrund der Logik. Eine solche Aussage, die aufgrund ihrer bloßen Form immer wahr ist, nennt man eine Tautologie.
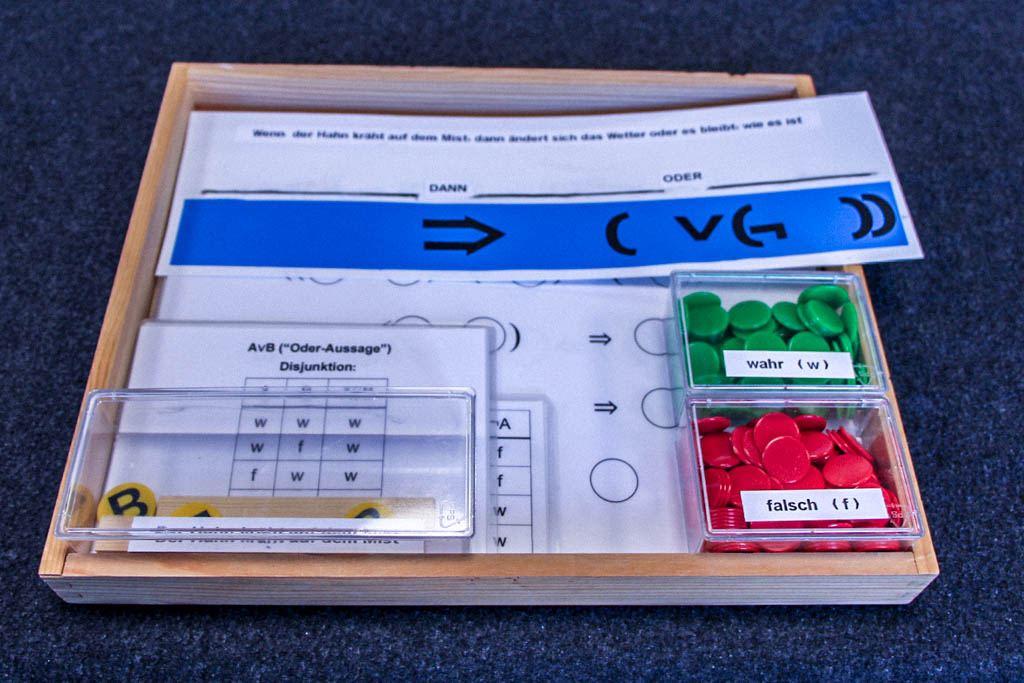
In der Mathothek gibt es ein Exponat, das den Einstieg in die formale Logik erleichtert:
Betrachten wir die Aussageform dieser Bauernregel und nutzen dabei das entsprechende Objekt aus der Mathothek:
Dieses Objekt zeigt uns, wie aus der bekannten Bauernregel eine Aussageform wird, die dann schließlich noch als eine Tautologie erkannt werden kann.
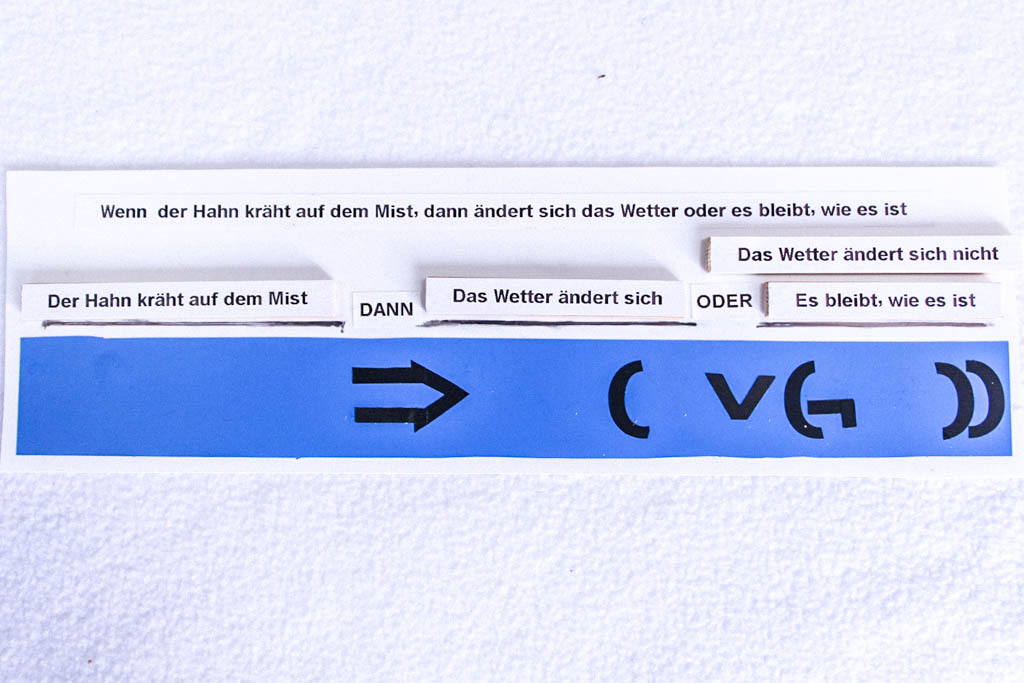
Die Aussage scheint zunächst aus drei Elementaraussagen zusammengesetzt zu sein, die wir durch die drei Platzhalter (Variablen) A, B und C ersetzen. “Der Hahn kräht auf dem Mist” → A, “Das Wetter ändert sich” → B und “Es bleibt, wie es ist” → C. Diese drei Elementaraussagen sind durch die logischen Junktoren wenn … , dann … , und oder verknüpft. Für sie gibt es die mathematischen Symbole ⇒ und ∨ mit klar definierten Funktionen. Diese sind klar festgelegt und auf den Verknüpfungstafeln des Exponats abzulesen. Damit erhalten wir die Formel A⇒(B∨C).
Man erkennt auch noch, dass “Es bleibt, wie es ist” die Verneinung von “Das Wetter ändert sich” darstellt. Damit ist C keine Elementaraussage, sondern äquivalent mit der Verneinung von B.
Das Zeichen ¬ bedeutet in der formalen Logik die Negation der folgenden Aussage, also gilt C⇔(¬B). Damit erhalten als Ergebnis die folgende Aussageform A⇒(B∨(¬B)).
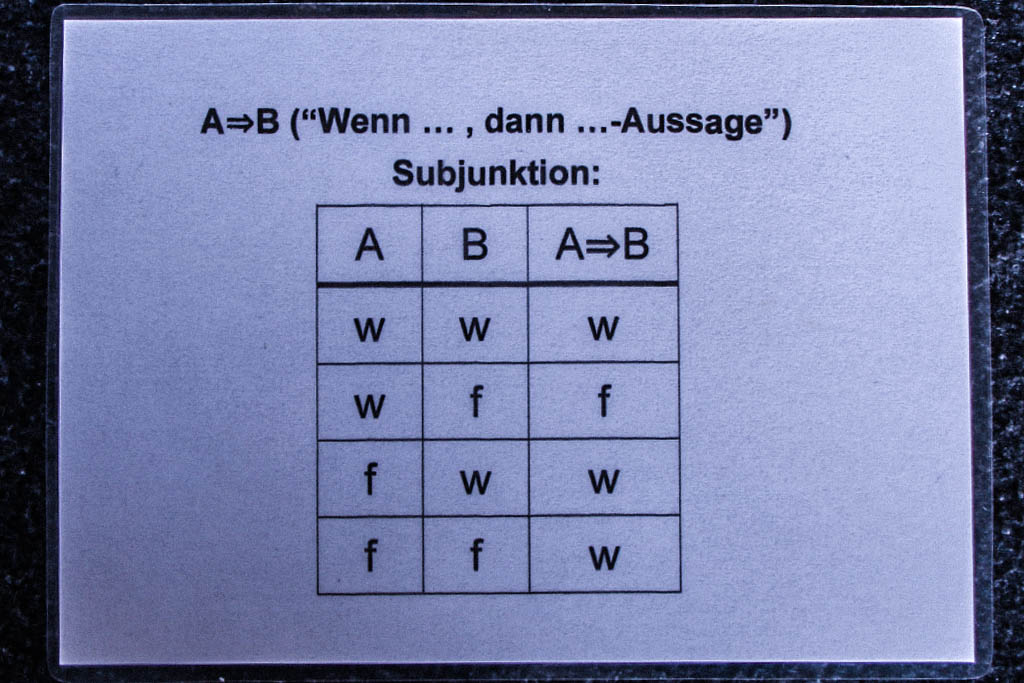
Nun können A und B unabhängig voneinander wahr (w) oder falsch (f) sein. Wir untersuchen dann den Wahrheitswert dieser Aussageform für alle vier möglichen Fälle: A ist wahr und B ist wahr, A ist wahr und B ist falsch, A ist falsch und B ist wahr sowie A ist falsch und B ist falsch. Aber dazu brauchen wir noch die Verknüpfungsregeln der drei logischen Junktoren.
Ganz wichtig beim Ermitteln des Wahrheitswertes ist die Einhaltung der richtigen Reihenfolge, also die Beachtung der Klammern. Aber das sind wir ja vom ganz normalen Rechnen schon längst gewohnt. Die Spalte B ist bei der Verknüpfungstafel für die Negation eigentlich unnötig, weil ¬ nur ein einstelliger Junktor ist, ¬A hat immer den entgegengesetzten Wahrheitswert von A und das völlig unabhängig vom Wahrheitswert von B. (Vgl. auch die Übersichtstafel weiter unten.)
- A ist wahr, B ist wahr, dann erhalten wir für die Aussageform A⇒(B∨(¬B)): w⇒(w∨(¬w)) und wegen ¬w ist f, bekommen wir dann w⇒(w∨f), w⇒w, also w.
- A ist wahr, B ist falsch, dann erhalten wir w⇒(f∨(¬f)), w⇒(f∨w), w⇒w und somit w.
- A ist falsch, B ist wahr, dann bekommen wir f⇒(w∨(¬w)), f⇒(w∨f), f⇒w und daher w.
- A ist falsch, B ist falsch, dann bekommen wir schrittweise f⇒(f∨(¬f)), f⇒(f∨w), f⇒w und somit w.
In der Junktorenlogik lässt sich der Wahrheitswert einer aus Elementaraussagen mit Junktoren korrekt zusammengefügten Aussage immer aus den Wahrheitswerten der Elementaraussagen und den Verknüpfungstafeln “berechnen”. Dabei spielt der semantische Inhalt (die Bedeutung) der Elementaraussagen keine Rolle mehr. Deswegen lassen sich auch inhaltlich lustige Beispiele bilden, z.B. “Wenn der Mond aus Käse ist, dann ist der Papst eine Frau.” oder “6+12=17 oder Paris ist die Hauptstadt Frankreichs”. Im ersten Fall liegt “f⇒f” vor, also ist die Aussage als Ganzes w. Im zweiten Fall haben wir f∨w, also ist auch hier die gesamte Aussage w.
Betrachten wir noch ein zweites Beispiel, das im Alltag oft missverständlich und auch oft falsch verwandt wird. Es geht um folgende Aussageform:
((¬A) v (¬B))⇔(¬(A∧B))
Es handelt sich hier um die Negation einer Und-Aussage. Ein Beispiel: Die Verneinung von “Ich habe Lust und Zeit.” ist nicht, wie man es oft hören kann, “Ich habe weder Lust, noch Zeit.” Korrekt lautet die Verneinung “Ich habe keine Lust oder ich habe keine Zeit.” Es könnte dann durchaus bedeuten, dass ich beides nicht habe oder dass ich Lust habe, aber keine Zeit oder Zeit habe, aber keine Lust verspüre.
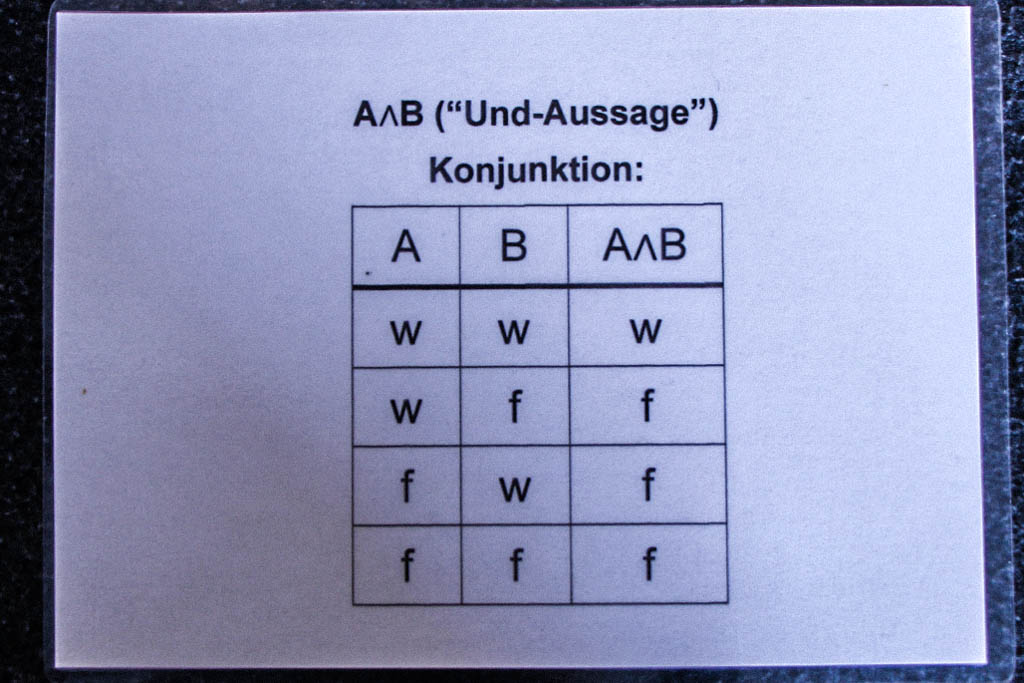
In dieser Aussageform treten zwei neue Junktoren auf. Das Symbol ∧ steht für “und” und ⇔ für “genau dann, wenn”. Dazu gibt es die beiden Verknüpfungstafeln:
Jetzt können wir überprüfen, ob die obige Verneinungsregel für eine Und-Aussage ((¬A)∨(¬B))⇔(¬(A∧B)) eine Tautologie ist:
- A ist wahr, B ist wahr: ((¬w)∨(¬w))⇔(¬(w∧w)), (f∨f)⇔(¬w), also f⇔f und damit w.
- A ist wahr, B ist falsch: ((¬w)∨(¬f))⇔(¬(w∧f)), (f∨w)⇔(¬f), also w⇔w und damit w.
- A ist falsch, B ist wahr: ((¬f)∨(¬w))⇔(¬(f∧w)), (w∨f)⇔(¬f), also w⇔w und damit w.
- A ist falsch, B ist falsch: ((¬f)∨(¬f))⇔(¬(f∧f)), (w∨w)⇔(¬f), also w⇔w, und somit w.
Diese Herleitung ist besonders einfach, wenn Du die entsprechende Folie bei diesem Exponat benutzt und zuvor die unten ausgeführten Beispiele nachvollzogen hast.
Bei allen Kombinationen erhalten wir – wie auch im ersten Beispiel – immer eine wahre Aussage und damit handelt es sich um eine allgemeingültige Aussageform, d.h. die obige Verneinungsregel ist eine Tautologie. Jede konkrete Aussage mit dieser logischen Form ist dann immer wahr.
Jede Aussageform, bei der man bei jeder möglichen Belegung der Aussagenvariablen mit w und f den Wert w erhält, nennt man eine Tautologie. Jede Aussage, die aus Elementaraussagen und Junktoren regelgerecht zusammengefügt ist und die Form einer Tautologie hat, ist aufgrund der Logik immer wahr.
Um solche Tautologien zu erkennen, gibt es bei diesem Exponat einige Versuche und Hilfsmittel:
Die weiter oben abgebildeten logischen Verknüpfungstafeln sind gute Hilfsmittel bei der Wahrheitswertberechnung der 17 Beispiele für Aussageformen, die als Versuchsmaterial zu diesem Objekt gehören. Die unten abgebildete Tabelle fasst die fünf logischen Verknüpfungen handlich und übersichtlich zusammen:
Die Platzhalter (Kreise) in den Aufgaben sind mit w (wahr) bzw. f (falsch) auszufüllen.
Dabei werden in der Startzeile nacheinander alle Möglichkeiten von wahr (grüner Chip) und falsch (roter Chip) eingesetzt. Für jede Einsetzung wird dann schrittweise der Wahrheitswert berechnet. Ist bei der jeweiligen Aussageform das Ergebnis in der letzten Zeile ein grüner Chip (wahr), so handelt es sich um eine Tautologie und nur dann.
Hier sind zunächst zwei Beispiele, die die einzelnen Schritte der “Berechnung” zeigen.
Erstes Beispiel: Regel der doppelten Verneinung.
Zunächst der Fall, dass A wahr ist. Anschließend der Fall, dass A falsch ist.
Da die Negation ein einstelliger Junktor ist, müssen hier nur zwei Möglichkeiten geprüft werden, nämlich A ist wahr (grün) und A ist falsch (rot). In beiden Fällen ist das Ergebnis grün, also ist Äquivalenz A⇔¬(¬A) immer wahr und damit eine Tautologie.
Zweites Beispiel: Widerspruchsregel
A und B sind beide wahr.
A ist wahr und B ist falsch.
A ist falsch und B ist wahr.
A ist falsch und B ist falsch.
In allen vier Fällen ist das Ergebnis wahr. Es handelt sich also um eine Tautologie.
Die tautologischen Formeln liefern uns die grundlegenden logischen Schlussregeln. So ergibt sich aus der obigen Tautologie ((A⇒B)∧(¬B))⇒(¬A) das folgende Schlussschema:
Wenn es wahr ist, dass aus A B folgt, und andererseits B falsch ist, d.h. die Verneinung von B wahr ist, dann kann A nicht wahr sein.
Machen wir ein konkretes Beispiel dafür. “Wenn es eben geregnet hätte, wäre der (nicht überdachte) Schulhof nass. Der Schulhof ist aber trocken. Also kann es nicht geregnet haben.”
Noch ein weiteres Beispiel für eine Tautologie: Kontrapositionsregel
Dieses Exponat zur Junktorenlogik soll einen kleinen Ausflug in die formale Logik ermöglichen und damit zeigen, dass dem Computer durch Algorithmen beispielsweise die Junktorenlogik beigebracht werden kann.
Es ist natürlich die Verbindung unserer “Rot-Grün-Logik” mit ihren beiden Werten wahr und falsch zum Binärsystem mit seinen beiden Ziffern 0 und 1 auffällig. Aber es ist nicht nur diese Ähnlichkeit interessant, sondern auch die Beziehung der Verknüpfungen von ∨ und ∧ zu + und ⋅, den beiden Verknüpfungen von 0 und 1 im Binärsystem. Dazu vergleichen wir die beiden Paare von Verknüpfungstafeln:
1⋅1=1 1⋅0=0 0⋅1=0 0⋅0=0 w∧w=w w∧f=f f∧w=f f∧f=f
1+1=10 1+0=1 0+1=1 0+0=0 w∨w=w w∨f=w f∨w=w f∨f=f
Der einzige Unterschied tritt bei der binären Addition 1+1=10 auf. Das Problem wird dadurch gelöst, dass man den “Übertrag” dieser binären Addition nimmt: 1+1=1.
Es gibt noch eine Parallele zu den Verknüpfungstafeln der Junktoren ∧ und ∨. Wenn M eine beliebige Menge von Elementen ist, die nicht die leere Menge {} ist, ∩ das Zeichen für die Schnittmenge und ∪ das für die Vereinigungsmenge, dann gelten folgende Beziehungen:
M∩M=M M∩{}={} {}∩M={} {}∩{}={}
M∪M=M M∪{}=M {}∪M=M {}∪{}={}
Wenn Du mehr über diese Zusammenhänge wissen willst, so kannst Du Dich mit dem Thema “Boole’sche Algebra” bereichern.
Besonders interessant wird es, wenn man auch Aussageformen betrachtet, die Es gibt x mit …– und Für alle x gilt …– Aussagen” verwenden. Diesen Bereich der formalen Logik ist gerade in der Mathematik besonders wichtig. Vergleiche einmal die beiden folgenden Beispiele.
- Für alle x gibt es ein y mit “y ist der Vater von x”.
- Es gibt ein y für alle x mit “y ist der Vater von x”.
Während die erste Behauptung wahr und unproblematisch ist, ist die zweite Aussage allenfalls für überzeugte Christen mit Gott-Vater akzeptabel.
Zu den Regeln der Junktorenlogik kommen hier in der Prädikatenlogik zwei weitere dazu, nämlich die Negation von “Für alle” und “Es gibt”:
- ¬Für alle x gilt A(x) ist äquivalent zu Es gibt ein x mit ¬A(x)
- ¬Es gibt ein x mit A(x) ist äquivalent zu Für alle x gilt ¬A(x)
Betrachten wir als Beispiel das offensichtlich falsche der beiden Eingangsbeispiele.
¬Es gibt ein y für alle x mit “y ist der Vater von x”
Für alle x (¬Für alle y gilt “y ist der Vater von x”
Für alle x gibt es ein y mit ¬”y ist der Vater von x”
Für alle x gibt es ein y mit “y ist nicht der Vater von x”
Ganz wichtig dabei ist, dass in der Mathematik und ihrer Logik “Es gibt ein x …” immer die Existenz von wenigstens einem behauptet und nicht von exakt einem.
Versuche bei den nächsten Beispielen beide Aussagen über natürliche Zahlen (={1, 2, 3, 4, … }) umgangssprachlich zu formulieren und zu sagen, welche wahr und welche falsch ist.
- Für alle n gibt es ein m so, dass m≤n gilt.
- Es gibt ein m, sodass für alle n gilt m≤n.
Wenn Dir die Begegnung mit der Junktorenlogik und der Logik insgesamt Spaß macht, dann kannst Du Dich auch noch durch ein weiteres Objekt der Mathothek über Antinomien und Paradoxien herausfordern lassen:
Es gibt noch einige Exponate, in deren Einkleidung die Logik eine besondere Rolle spielt:
“Goofy als Wegweiser.”
“Logik kann Leben retten.”
“Blau, weiß oder gemischt?”
Hier noch ein sowohl logisch wie auch geschichtlich interessantes Objekt, das “Barbier-Problem”.