Wie können wir helfen?
Die Künstlerin Ingrid Hornef aus Hofheim hat sich in ihrem künstlerischen Schaffen oft mit mathematischen Themen auseinandergesetzt. So auch mit den Erscheinungen von Ordnung und Zufall. Es gibt zwei Exponate in der Mathothek, die Arbeiten von ihr nachempfunden sind. An anderer Stelle dieses Katalogs geht es um die Kreation von einmaligen Bildern aus ausgewählten Motiven und einem Würfel.
Ein weiteres Exponat der Mathothek, das von einem Werk Ingrid Hornefs Konkreter Kunst besteht aus zehn identischer Brücken, die aus je sechs Holzwürfeln zusammengeklebt wurden:
Mit diesen Bausteinen kann eine sehr große Zahl von Objekten gebaut werden. Die einfachen “handfesten” Holzteile werden durch die kreative Phantasie des Menschen zu einer Fülle von konkreter Kunst:
Faszinierend ist bei diesem künstlerischen Schaffen, wie hier einfache konkrete Formen aus natürlichem Material einerseits und geistige Schöpfungskraft spielerisch fruchtbar werden, und zwar für jeden, der sich darauf einlässt.
Oft kann man in der Mathothek beobachten, dass solche Exponate, wie sie hier vorgestellt werden, von vielen jüngeren Besuchern nicht zuletzt wegen ihrer meditativen Wirkung ausgewählt werden.
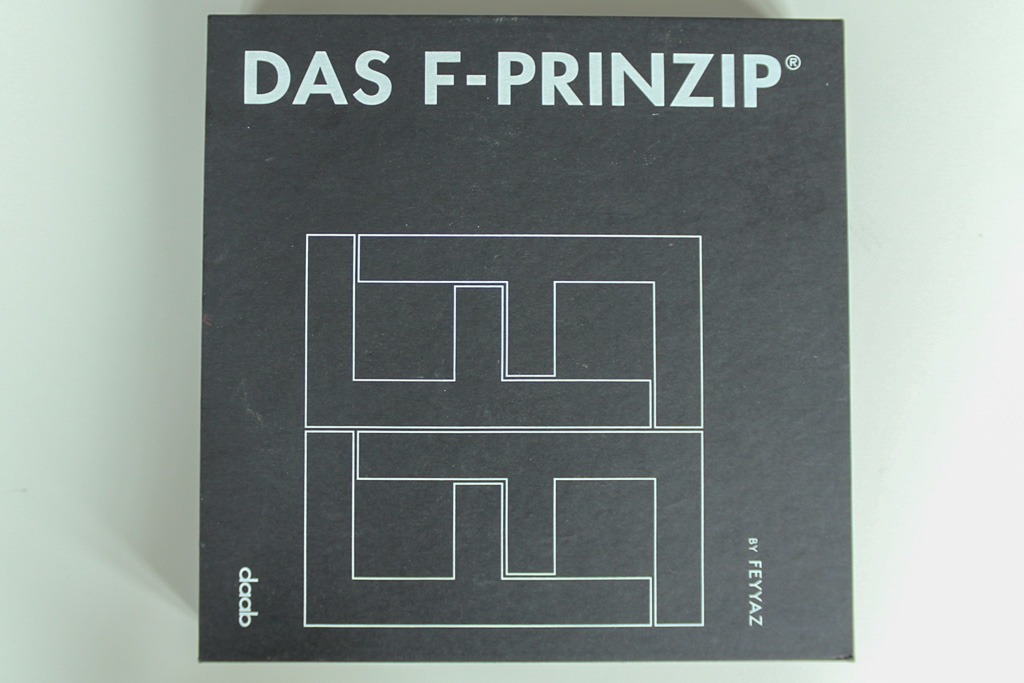
Ein weiteres Angebot für Besucher der Mathothek, sich spielerisch und kreativ mit Konkreter Kunst zu beschäftigen, ist Das F-Prinzip von Feyyaz. Im Begleitheft schreibt Kay von Keitz: “Hier wird der Buchstabe F zum Prinzip erhoben, zu einer modularen Konstruktionsfigur, die mit ihrer unvermuteten Vielzahl kombinatorischer Möglichkeiten zu beeindrucken weiß. Der Künstler Feyyaz hat den Anfangsbuchstaben seines Namens schon vor vielen Jahren von seiner eigentlichen Bestimmung befreit und der blickweitenden Abstraktion zugeführt. Nun aber eine ausschließlich zufällige und damit beliebige alliteratorische Zwangsläufigkeit zu unterstellen, wäre ganz falsch, denn das F birgt – für jeden überprüfbar – weit größere konstruktive Potenziale als alle anderen Buchstaben unseres Alphabets. Und da der Mensch, zumindest der Mensch der Moderne, das Prinzipielle, Serielle und Modulare besonders schätzt, forscht er immer wieder nach Quellen für systematische Ableitungen dieser Art, die er technisch, historisch, philosophisch, symbolisch und natürlich ästhetisch zu begründen sucht. So unbelastet und setzungsfreudig wie Feyyaz haben bisher allerdings wenige auf diesem Gebiet gehandelt. Was ist schon ein Kreis oder ein Quadrat oder ein Corbusier’scher Modulor gegen ein perfekt proportioniertes F. Wer mit diesen schönen hölzernen Fs zu spielen beginnt, wird das schnell feststellen – und sich gerne an die glücklichen Stunden erinnern, die er als Kind mit Bauklötzen verbracht hat.”
Der Architekt Stephen Williams betont die Unterstützung, die dieses Objekt leisten kann, um räumliche Bezüge zu erkunden, aber auch die Herausforderung, die Proportionen zwischen fester Masse und leerem Raum aufeinander abzustimmen. Was immer wieder zu erneuten Umrangierungen führt. Er weist darauf hin, dass die Lage des kürzeren Querbalkens, weil er nicht in der Mitte des senkrechten Balkens liegt, zu einem wunderbaren Ungleichgewicht führt, das der Spieler auszugleichen versucht. Da die Blöcke keine Maßstäbe aufweisen, können sie als Häuserblocks, Sitzgruppe oder begrenzende Mäuerchen in der Phantasie des Spielers dienen.
“Wie man das Ganze interpretiert, hängt von der jeweiligen Vorstellungskraft und Auffassungsgabe des Spielers ab. Mit den Formen des “F-Prinzips” entdeckt man eine neue Dimension der Wahrnehmung.”
“Indem der Spieler die Formen so arrangiert, dass sie eine perfekte oder besser noch eine imperfekte Komposition ergeben, lernt er die Problematik und den Kampf aller Designer kennen, die sich der fundamentalen Schwierigkeit stellen müssen, eine gute Lösung für ein räumliches Konzept zu finden.”
Vier Beispiele für ebene Formen:
Augenfällig ist es, dass die Ergebnisse bewusst oder zufällig Symmetrien aufweisen, obwohl das F als Grundelement keine Symmetrie besitzt.
Es folgen noch zwei räumliche Gebilde aus den vier Fs:
Nur selber machen ist schöner!