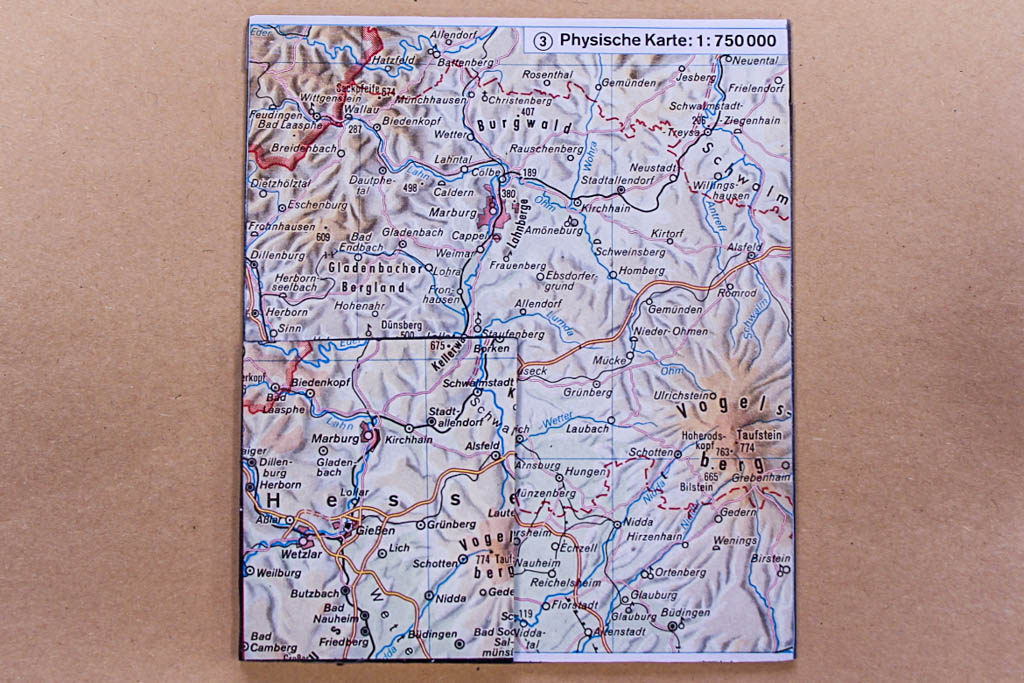
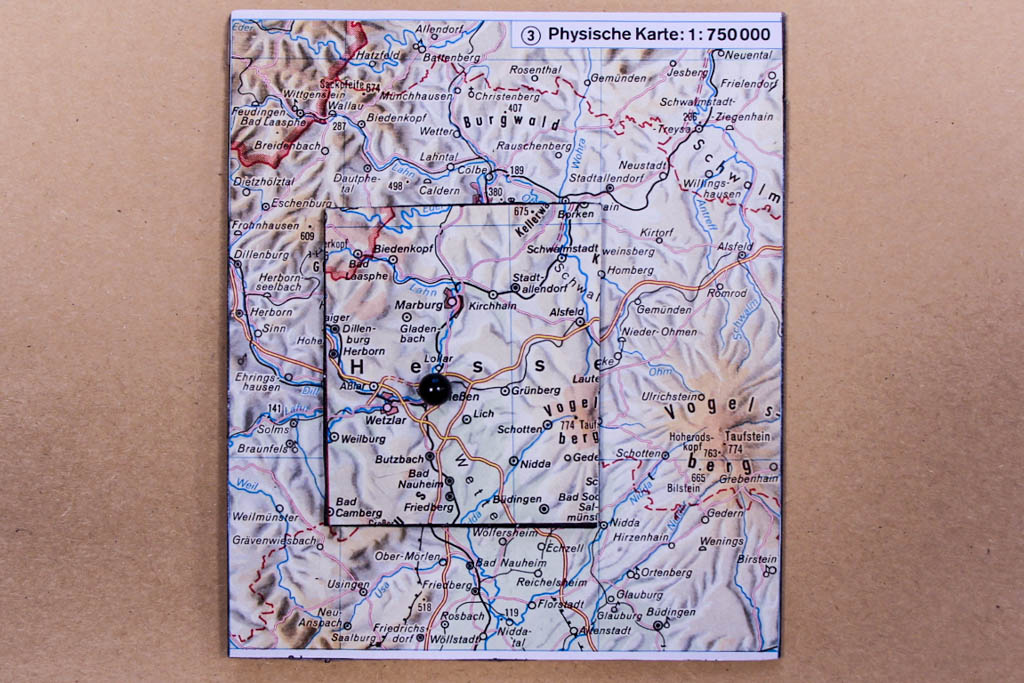
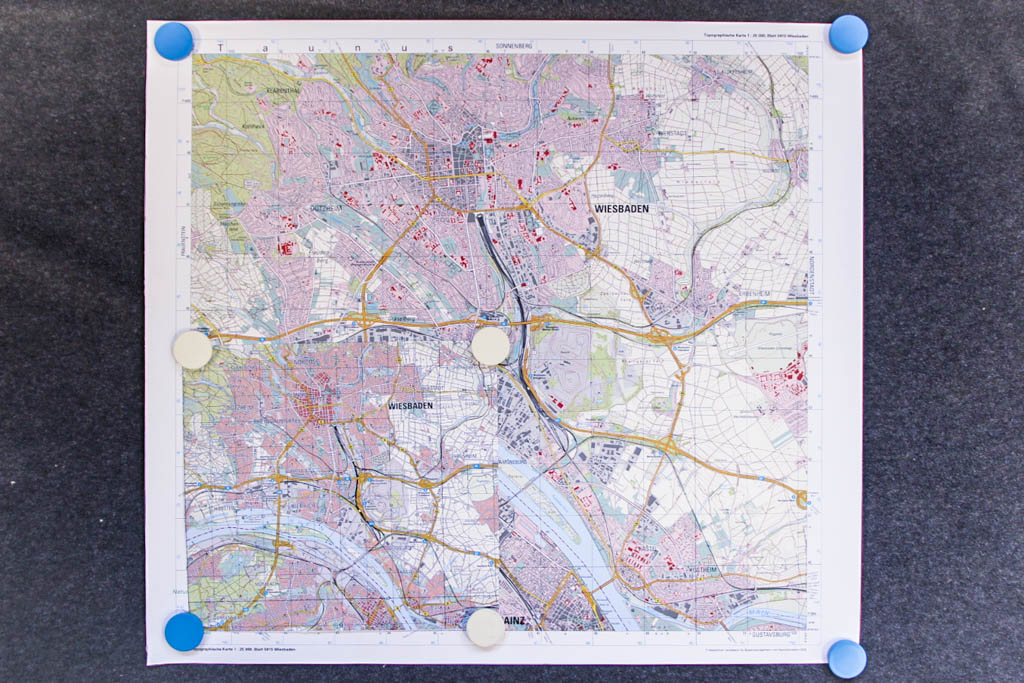
Bei dem ersten Beispiel von Fixpunkten gehen wir mithilfe von Karten sehr pragmatisch vor. Wir haben hier einmal einen Ausschnitt aus einer physischen Karte von Mittelhessen im Maßstab 1:750.000 und denselben Ausschnitt in einer weiteren Karte im Maßstab 1:1.500.000.
Man sieht, dass die kleinere Karte (1:1.500.000) ein Viertel der Fläche der größeren (1:750.000) ausmacht, aber genau denselben Bereich Mittelhessens darstellt.
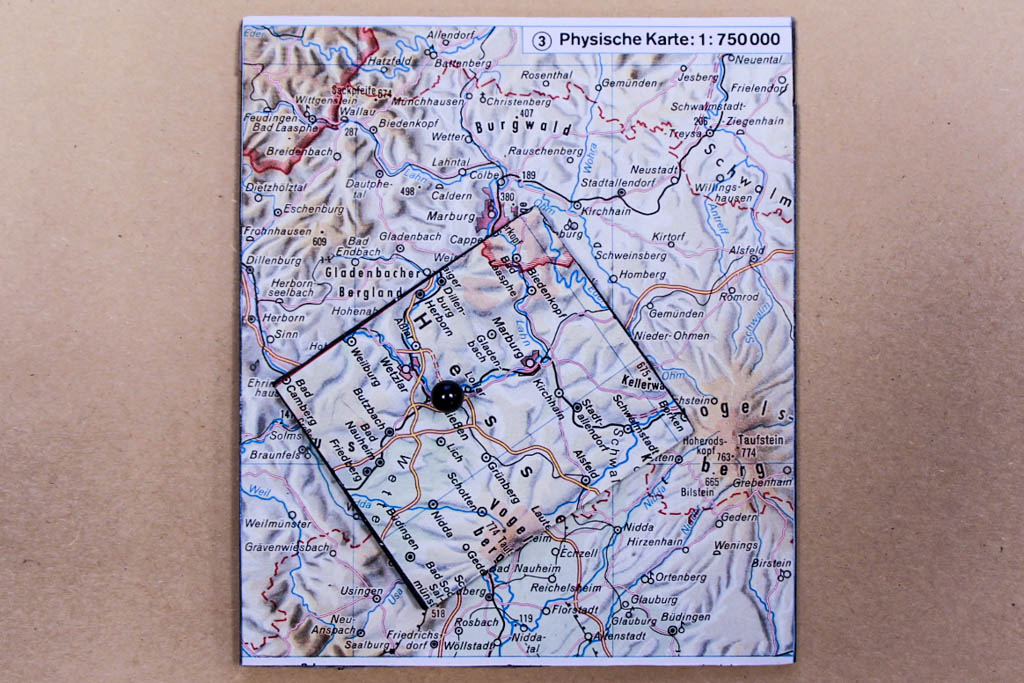
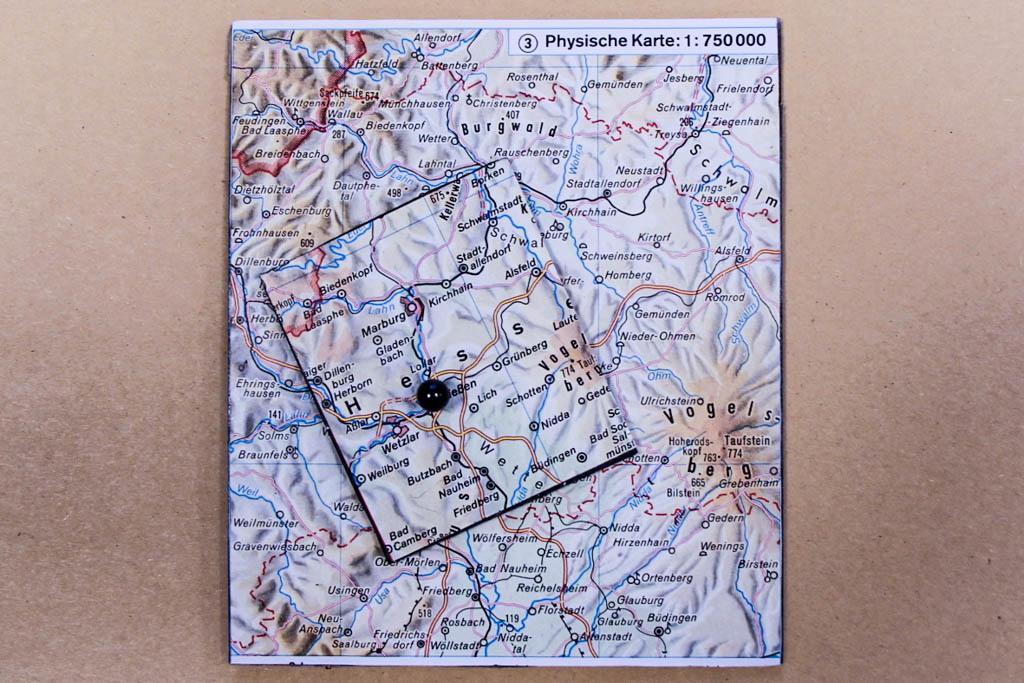
Die Behauptung ist nun, dass es immer einen Fixpunkt gibt, wenn man die kleinere Karte so auf die größere legt, dass kein Punkt der kleinen Karte außerhalb der großen liegt. Fixpunkt bedeutet hier, dass ein Punkt (Ort) der kleineren Karte genau über dem entsprechenden Punkt (Ort) der großen Karte liegt. Die Pinnnadel mit dem schwarzen Kopf verbindet Gießen auf beiden Karten. Das bleibt auch wahr, wenn wir die kleine Karte nicht parallel zur großen legen, sondern beliebig um die Achse der Nadel drehen.
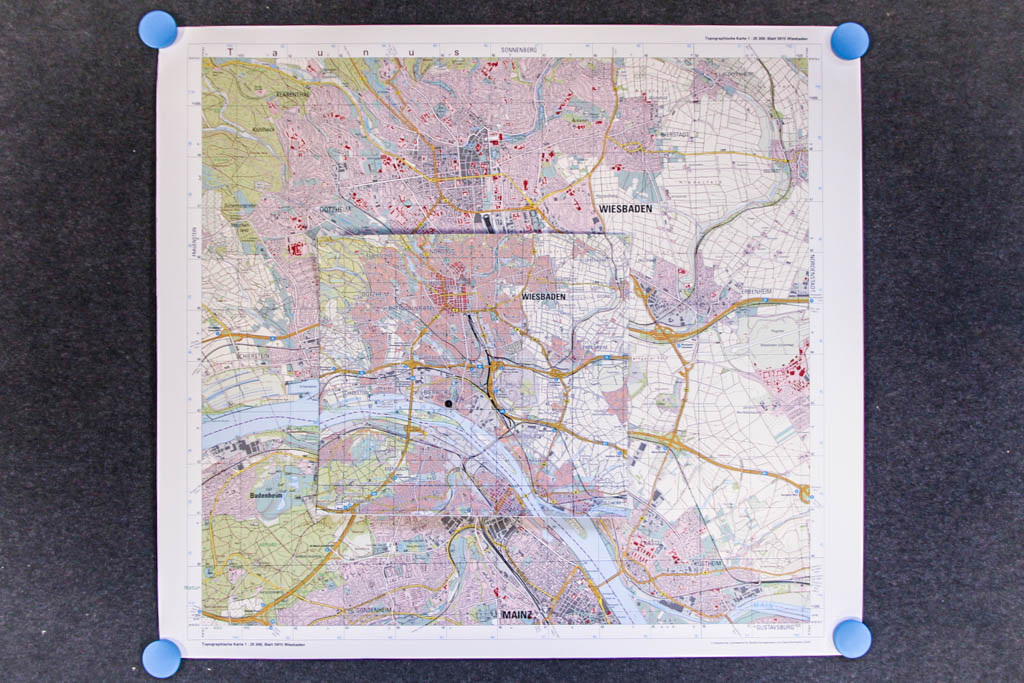
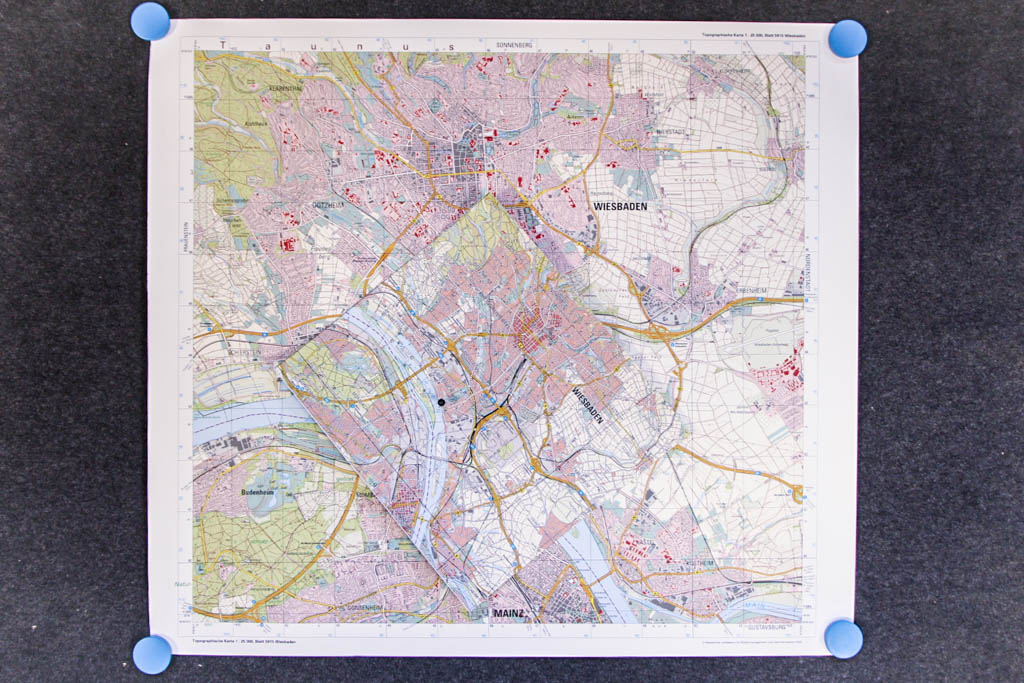
Wir können mit einem zweiten Beispiel dies noch einmal veranschaulichen. In diesem Falle nehmen wir zwei topografische Karten von Wiesbaden im Maßstab 1:25.000 und 1:50.000. Die topografische Karte 1:50.000 teilen wir in vier kongruente Teile, von denen der Ausschnitt in der linken unteren Ecke mit dem Inhalt der topografischen Karte 1:25.000 entspricht.
So wie im ersten Fall „Gießen“ dem Fixpunkt entsprach, liegen jetzt die beiden Karten so aufeinander, dass jetzt das „Schloss Biebrich am Rhein“ (schwarzer Punkt) dem Fixpunkt entspricht.
Nun die Frage: Warum ist das so? Warum muss es bei jeder solcher Lage der Karten einen solchen Fixpunkt geben? Es gibt dazu verschiedene mathematische Beweise. Wir versuchen hier mit einem Gedankenexperiment die Frage pragmatisch zu lösen: Denken wir uns zunächst beide Karten jeweils im größeren Maßstab, 1:750.000 bzw. 1:25.000, deckend aufeinandergelegt. In diesem Moment gibt es natürlich nur Fixpunkte. Für die weiteren Überlegungen können wir nun jeden beliebigen Ort auswählen und gedanklich eine Pinnnadel an dieser Stelle durch beide Karten stechen. Anschließend lassen wir die obere Karte in Gedanken auf die Karte mit dem kleineren Maßstab (1:1.500.000 bzw. 1:50.000) schrumpfen. Es gibt nun nur noch einen Fixpunkt, nämlich denjenigen, in dem unsere Nadel steckt. Da es keine Ausnahmen gibt und wir uns dieses Vorgehen für jeden Punkt vorstellen können, gilt unsere Überlegung für alle Punkte unserer kleinen Karte. Natürlich können wir diese nun auch noch um die Pinnnadel beliebig drehen, der Fixpunkt bleibt. Umgekehrt folgt aus der Annahme, es gäbe keinen Fixpunkt, ein Widerspruch: Wir vergrößern unsere kleine Karte bis zur Größe der großen Karte und legen sie exakt deckend aufeinander. So muss es mindesten einen Punkt geben, an dem auf jeder Karte ein anderer Ort liegt. Das wäre aber ein Widerspruch zur Identität der beiden Karten.
Die Erkenntnisse dieses Gedankenexperiments lassen sich natürlich auf andere „Karten“ übertragen, z.B. Bilder, Textseiten, Fotos, gemustertes Papier usw.
Bei der Lottoziehung 6 aus 49 werden die sechs Kugeln mit den Gewinnzahlen zunächst gezogen und dann der Größe nach geordnet, weil es ja beim Gewinnen nicht darauf ankommt, dass der Spieler auch noch die Reihenfolge vorhersagen muss. Nun kann es ja durchaus sein, dass eine Kugel so fällt, dass sie gleich am richtigen Platz zu liegen kommt, es sich also um einen Fixpunkt handelt. Wie groß ist die durchschnittliche Anzahl solcher Fixpunkte pro Ziehung?
Im Zeitraum vom 9.10.1953 bis 31.10.2016 gab es 5.548 Ziehungen, und zwar traten in diesem Zeitraum die Anzahl der Fixpunkte bei der entsprechenden Anzahl von Ziehungen auf:
Anzahl der Fixpunkte: 0 1 2 3 4 5 6
Anzahl der Ziehungen: 2067 2000 1035 520 117 0 9
Berechnen wir nun die durchschnittliche Anzahl der aufgetretenen Fixpunkte:
0⋅2067+1⋅2000+2⋅1035+3⋅320+4⋅117+5⋅0+6⋅9=5552 und 5552:5548=1,000720981
Das Ergebnis dieser Auswertung ist doch sehr erstaunlich, fällt im Durchschnitt der Lottoziehungen doch nur eine Kugel auf ihren richtigen Platz, während fünf Kugeln durchschnittlich umgeordnet werden müssen.
In der Mathothek gibt es eine Variante des letzten Experiments: Es besteht aus 12 kleinen runden Spanschachteln.
Jeder Boden und Deckel trägt eine der Zahlen von 1 bis 12. Das Experiment besteht darin, dass Deckel und Böden getrennt und bunt vermischt werden. Anschließend wird rein zufällig je ein Deckel und ein Boden zu einer Schachtel zusammengetan. Falls die beiden Zahlen von Deckel und Boden übereinstimmen, so ist das ein Fixpunkt. Auch bei diesem Experiment zeigt es sich, dass auf längere Sicht, die durchschnittliche Anzahl der auftretenden Fixpunkte eins ist.
Es gibt noch eine zweite Variante mit einer größeren Anzahl von kleinen Dosen aus Plastik, deren Boden und Deckel jeweils das gleiche Blumenmotiv tragen.
Diese Experimente sind in der Mathematik Einkleidungen des sog. Rencontre-Problems, der Frage nach den Fixpunkten von Permutationen. Die bekannteste Einkleidung ist das sog. Sekretärinnen-Problem. Dabei geht es darum, dass eine Sekretärin in großer Eile eine Anzahl adressierte Schreiben rein zufällig in vorbereitete Umschläge steckt. Bei vielen Besuchern der Mathothek, die eines der obigen Experimente mehrfach durchführen, lösen die Beobachtungen Erstaunen und reichlich Diskussionen aus. Vielen erscheint es zunächst intuitiv richtig, dass die Gleichheit von Deckel und Boden öfters auftritt, wenn man viele Wiederholungen des Experimentes macht und dass damit auch die durchschnittliche Anzahl der Fixpunkte wachsen müsste.
Von einem Fixpunkt spricht man allgemein in der Mathematik im Zusammenhang mit Zuordnungen, wenn ein Punkt (eine Zahl, ein Element usw.) und sein Bildpunkt (seine zugeordnete Zahl, sein zugeordnetes Element) übereinstimmen.
Hierzu benutzen wir ein Exponat der Mathothek, mit dem wir uns die Deckabbildungen eines gleichseitigen Dreiecks veranschaulichen können.
Wir betrachten ein geometrisches Beispiel, bei dem wir ein gleichseitiges Dreieck mit den Ecken ABC und dessen Deck- oder Symmetrieabbildungen zugrundelegen. Für dieses gleichseitige Dreieck gibt es folgende Symmetrieabbildungen: drei Achsenspiegelungen und drei Drehungen.
Die Spiegelung an der Symmetrieachse durch A:
Die Spiegelung an der Symmetrieachse durch B:
Die Spiegelung an der Symmetrieachse durch C:
Die Drehung um 240° ( im mathematisch positiven Sinn, gegen den Uhrzeigersinn) am Mittelpunkt:
Die Drehung um 120° am Mittelpunkt:
Die Drehung um 360° (=0°) oder identische Abbildung:
Nehmen wir die Fläche des Dreiecks, so gibt es bei den einzelnen Symmetrieabbildungen verschiedene Fixpunktmengen, der Mittelpunkt (das Symmetriezentrum) ist natürlich in jedem Fall dabei. Genauso auch die Punkte auf den Spiegelungsachsen. Wir beschränken uns auf die Eckpunkte des Dreiecks, A, B und C, die das Dreieck festlegen. Dann erhalten wir das folgende Ergebnis. Bei den Spiegelungen wird jeweils einer der Eckpunkte auf sich abgebildet, bei den Drehungen sind es zweimal keiner und einmal – bei der identischen Abbildung alle drei, die fest bleiben. Das geometrische Beispiel lässt sich auch leicht in das folgende kombinatorische Beispiel übersetzen.
Betrachtet man alle möglichen „Anordnungen“ (Permutationen) von A, B und C, nämlich ABC, ACB, BAC, BCA, CAB und CBA, dann gibt es bei ACB, BAC und CBA jeweils genau einen Fixpunkt, bei BCA und CAB keinen und bei ABC drei Fixpunkte. Die Anordnungen BCA und CAB bezeichnet man auch als fixpunktfreie Permutationen. Die durchschnittliche Anzahl von Fixpunkten beträgt (2⋅0+3⋅1+1⋅3):6=1.
Vier unterscheidbare Objekte, z.B. die Buchstaben A, B, C und D, lassen sich auf 4⋅3⋅2⋅1=24 Arten anordnen:
ABCD ABDC ACBD ACDB ADBC ADCB
BACD BADC BCAD BCDA BDAC BDCA
CABD CADB CBAD CBDA CDAB CDBA
DABC DACB DBAC DBCA DCAB DCBA
Hier gibt es 9 Permutationen mit 0 Fixpunkten, 8 mit 1 Fixpunkt, 6 mit 2, 0 mit 3 und 1 Permutation mit 4 Fixpunkten. Die durchschnittliche Anzahl von Fixpunkten beträgt (0⋅9+1⋅8+2⋅6+4⋅1):24=24:24=1.
Natürlich sind diese beiden Beispiele aus der Kombinatorik noch kein Beweis für die Gültigkeit einer Verallgemeinerung der Anzahl durchschnittlicher Fixpunkte bei Permutationen, was hier auch nicht zu tun beabsichtigt ist. Aber die verschiedenen Zugänge – pragmatisch, experimentell, geometrisch und kombinatorisch – der entsprechenden Exponate liefern interessante und anregende Erfahrungen und machen vielleicht auch Lust darauf, tiefer in das Rencontre-Problem, der Untersuchung der Wahrscheinlichkeit von Fixpunkten, einzusteigen.