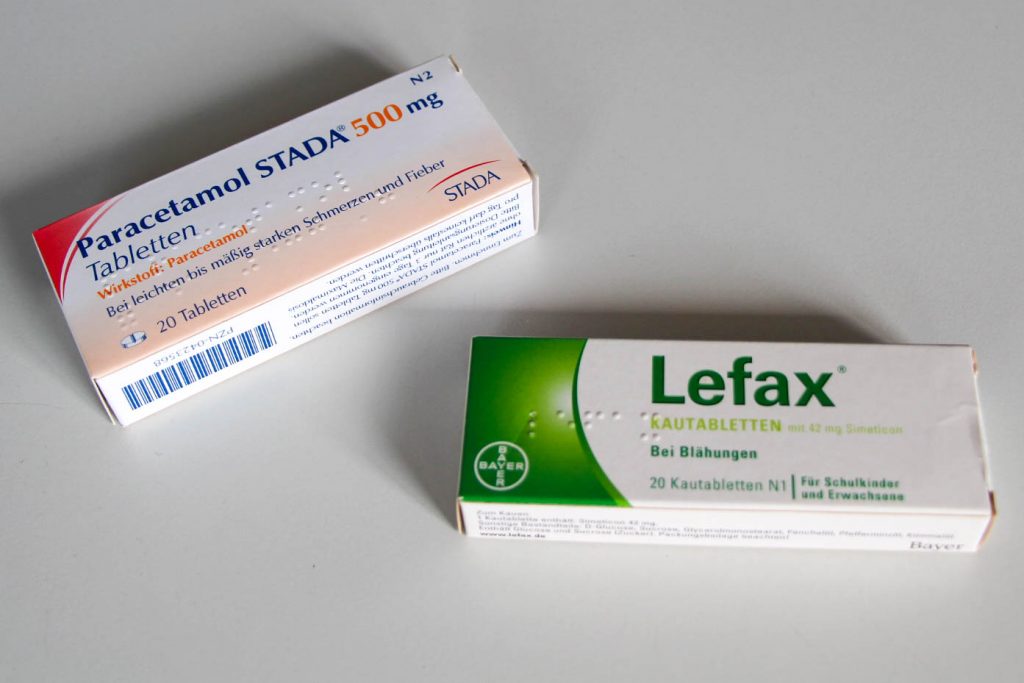
Viele Besucher sind es nicht, die in die Mathothek kommen und bisher von der Brailleschrift mehr als nur Mal gehört haben. Auf einer Postkarte sind die Buchstaben und Zahlen sowohl normal lesbar als auch in der mit den Fingerkuppen tastbaren Blindenschrift zusammengestellt. Mithilfe einiger Arzneimittelverpackungen ist der praktische Umgang mit dieser fühlbaren Schrift erfahrbar.
Gleichzeitig wird den sehenden Besuchern klar, wie wichtig die Existenz dieser Schrift für Blinde und stark sehbehinderte Menschen gerade auch im Alltag ist. Diese tastbare Schrift wurde 1825 von dem Franzosen Luis Braille entwickelt. Er entdeckte, dass sechs Punkte ausreichend sind, um das Alphabet, die Zahlen und andere notwendige Zeichen darzustellen.
Hier beginnt der mathematische Teil der Geschichte. Warum lassen sich alle notwendigen Zeichen mit nur sechs Punkten wiedergeben?
Es handelt sich bei dem Prinzip von Braille eigentlich nicht um sechs Punkte, sondern um sechs Stellen oder Plätze. An jedem dieser sechs Stellen kann ein erhabener, mit der Fingerkuppe fühlbarer Punkt sein. Bei dem Exponat in der Mathothek sind diese sechs Plätze die Vertiefungen in dem Eierkarton und die erhabenen Punkte werden von Plastikeiern repräsentiert. Im ersten Fall sind alle sechs Plätze besetzt. Im zweiten Fall ist von den sechs Plätzen nur ein bestimmter Platz belegt. Je nachdem, wie viele Eier und an welchen Plätzen die Eier stecken, hat das entsprechende Braillezeichen eine andere Bedeutung. Es gibt somit sechs Möglichkeiten, wo das eine Ei liegen kann. Es gibt natürlich auch eine Möglichkeit, bei der alle Plätze frei bleiben.
Hier sind fünf weitere Möglichkeiten abgebildet, bei denen beispielsweise zwei, drei, vier bzw. fünf Plätze besetzt sind. Ein Platz oben links besetzt, bedeutet in der Blindenschrift den Buchstaben A. Die weiteren Kombinationen bedeuten die Buchstaben B, C und G. Das letzte Beispiel steht für die Buchstabenkombination SCH.
Diese beiden Zeichen stehen zusammen für die Ziffer 1. Die nächsten beiden bedeuten die Ziffern 2 und 3.
In der Brailleschrift gibt es keine eigenständigen Zahlzeichen, sondern man benutzt das Alphabet. Im Gegensatz zu antiken Zahlschreibweisen mit den Buchstaben eines Alphabets bedient sich die Blindenschrift des Dezimalsystems und benutzt nur die ersten zehn Buchstaben mit einem vorgestelltem Zahlenzeichen.
Warum war nun Luis Brille sicher, dass mit dieser Methode der Darstellung genügend Zeichen zur Verfügung standen? Das ist eine mathematische Aufgabe, und zwar aus der Kombinatorik. Man könnte nun alle Möglichkeiten ausprobieren und zählen. Das wäre zu umständlich und könnte schnell zu Fehlern führen. Also machen wir es systematisch, d.h. mathematisch. Für jeden der Plätze gilt, dass dort ein Ei liegen kann oder nicht, und diese zwei Möglichkeiten bestehen für jeden der sechs Plätze unabhängig von den anderen. Also gibt es 2 Möglichkeiten für den 1. Platz, wobei sich bei jeder Entscheidung zum 1. Platz wieder 2 Möglichkeiten für den 2. Platz ergeben, damit 2⋅2 Möglichkeiten für die beiden ersten Plätze. Bei jeder dieser vier Möglichkeiten gibt es nun wieder 2 Möglichkeiten für den 3. Platz, also gibt es für die Belegung der ersten drei Plätzen 2⋅2⋅2=8 Möglichkeiten. Insgesamt gibt es somit 2⋅2⋅2⋅2⋅2⋅2=26=64 Möglichkeiten für die Sechsereierkiste. Diese Anzahl reicht natürlich für Buchstaben und Ziffern sowie zahlreiche Sonderzeichen aus.
In der Kombinatorik spricht man hier von ungeordneten Stichproben ohne Wiederholung: Es werden aus sechs Plätzen k (k kann hier 0, 1, 2, 3, 4, 5 oder 6 sein) verschiedene Plätze ausgewählt. In welcher Reihenfolge sie ausgewählt und dann die „Eier“ hineingelegt werden, ist gleichgültig. Allerdings kann jeder Platz höchstens einmal belegt werden. Die Anzahl der Möglichkeiten beträgt dann 2k. Für diese Art kombinatorischer Stichproben gibt es überall und gerade auch im Alltag viele Beispiele.
Auch in der Mathothek können zahlreiche andere Exponate als Beispiele benutzt werden, so auch das Entropie-Spiel, wenn man beispielsweise die Anzahl der Mikrozustände ausrechnen will. Jede Belegung des 8×8-Bretts mit grünen und schwarzen Chips ist ein Mikrozustand. Alle Mikrozustände mit derselben Anzahl schwarzer Chips bilden einen Makrozustand. Da auf jedem der 8·8=64 Plätze ein grüner oder ein schwarzer Chip liegen kann, gibt es 264, also ca. 18 Trillionen Mikrozustände.
In der Würfelsammlung der Mathothek gibt es auch einen besonderen Würfel für Blinde oder stark Sehbehinderte. Mit der Brailleschrift verbindet ihn die Idee der fühlbaren Punkte, nicht aber die Darstellung der Zahlen. Das dürfte aber kein Nachteil sein.