
Das Glücksrad dreht sich und entscheidet zwischen zwei Personen A und B. Im täglichen Leben geht es ja oft um die Frage „Du oder Ich“. Wer muss den Abwasch machen? Wer bringt den Müll hinunter? Wer kriegt bei der Scheidung den Hund, oder wer geht mit ihm Gassi? Hier hilft ein Zufallsgerät, Streit zu vermeiden und einen neutralen Schlichter einzusetzen.
Die einfache Regel lautet, A und B entscheiden sich jeweils für den roten, blauen oder grünen Pfeil. Dann wird das Glücksrad in Bewegung gesetzt. Nachdem das Glücksrad stillsteht, zeigt jeder der beiden gewählten Pfeile auf eine der Zahlen eins, zwei oder drei. Wessen Pfeil auf die höhere Zahl zeigt, hat die Runde gewonnen.
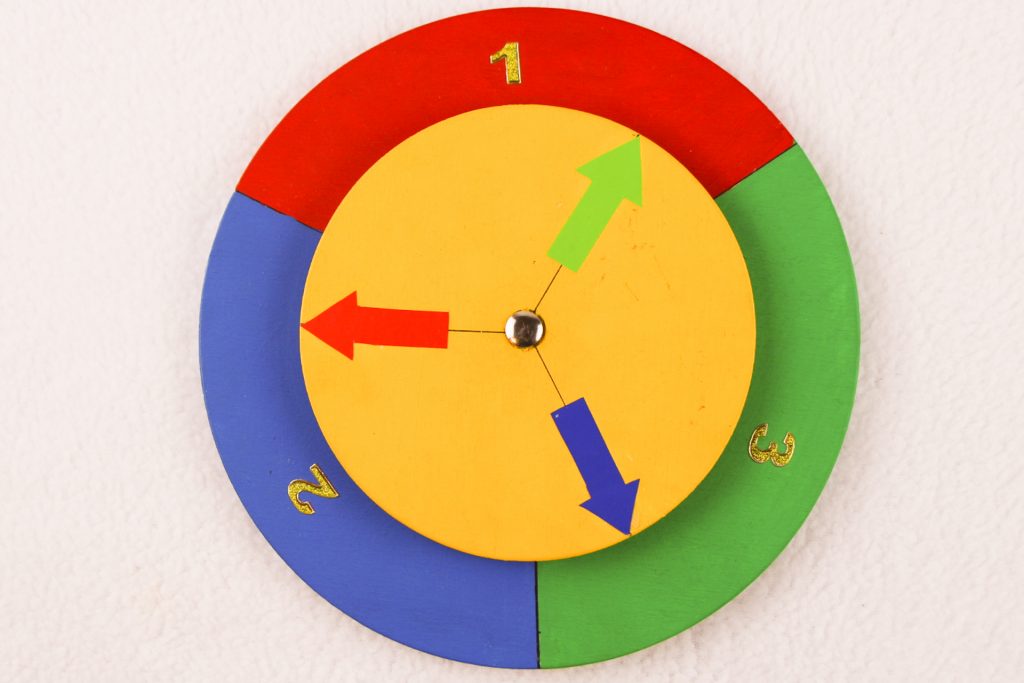
Nehmen wir an, dass A den blauen Pfeil gewählt hat und B den roten. Dann hätte A gewonnen, weil sein Pfeil auf die Drei zeigt und der von B auf die Zwei.
Nehmen wir an, dass A den grünen Pfeil gewählt hat und B den blauen, dann hätte natürlich B gewonnen.
Das sieht doch sehr gut aus für eine neutrale und zufällige Entscheidung.
Aber es sieht eben nur so aus. Blickt jemand durch, so lässt er den Konkurrenten zuerst wählen und entscheidet sich selbst für denjenigen Pfeil, der gegen den Uhrzeigersinn dem von dem ersten gewählten Pfeil am nächsten ist. Durch diese Strategie verdoppelt der Zweite die Wahrscheinlichkeit, dass er gewinnt.

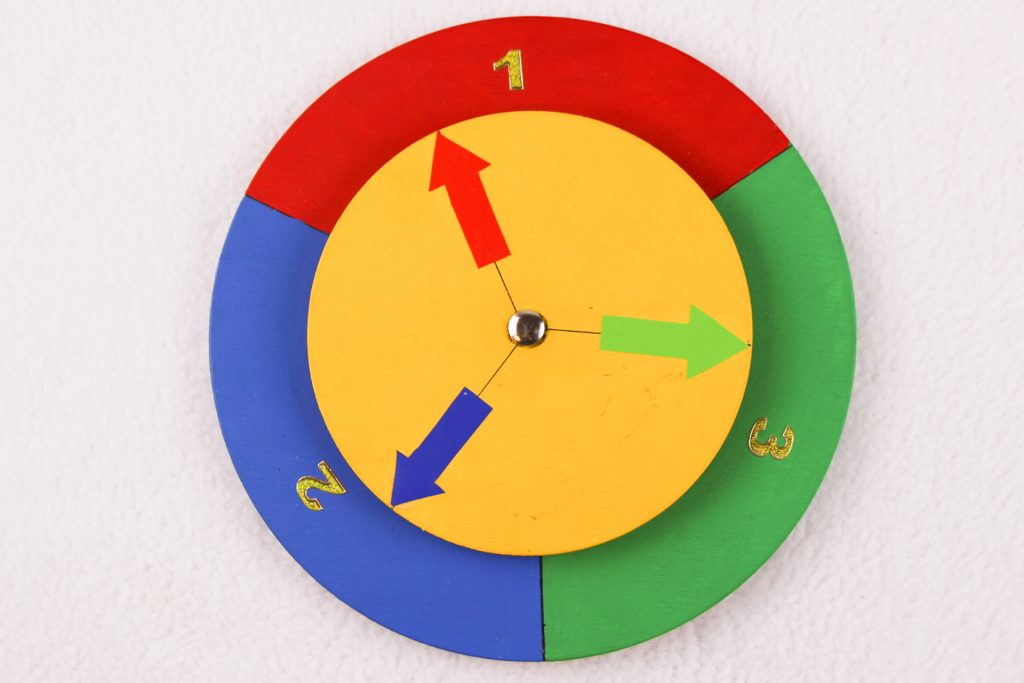


Warum ist das so? Wählt A den roten Pfeil, dann muss B entsprechend seiner Strategie den blauen wählen. Zeigt der rote Pfeil auf die Eins, zeigt der blaue auf die Zwei und zeigt der rote auf die Zwei, zeigt der blaue auf die Drei. In beiden Fällen gewinnt B. nur im Fall, dass der rote Pfeil auf die Drei zeigt, zeigt der blaue auf die Eins und B verliert. Also gewinnt B bei dieser Strategie in zwei von drei Möglichkeiten und verliert nur einmal. Er hat also eine doppelt so große Chance als A. Unfair! Es ist egal, was der Erste wählt, wenn der Zweite seine Entscheidung strategisch richtig trifft, hat er die doppelte Gewinnwahrscheinlichkeit.
Die vier Farben auf dem Holz haben nur dekorative Funktion.
Dieses Exponat der Mathothek ist gerade bei jüngeren Besuchern beliebt und ermöglicht es ihnen – auch ohne Vorkenntnisse – sich mit Wahrscheinlichkeiten auseinanderzusetzen. Es ist somit als Exponat ein Paradebeispiel für das Motto: „Mathothek – Mathematik begreifbar machen“.