Satellitenbilder des „blauen Planeten“ haben sich inzwischen in fast allen Köpfen seiner Bewohner fest als das Bild unserer Heimat im All etabliert. Trotzdem arbeiten wir im Alltag und bei kleinen Ausschnitten, z.B. als Stadtpläne, Wanderkarten oder Landkarten im größeren Maßstab, immer noch erfolgreich mit planaren Darstellungen von eigentlich kugelförmigen Ausschnitten unserer Erdoberfläche.
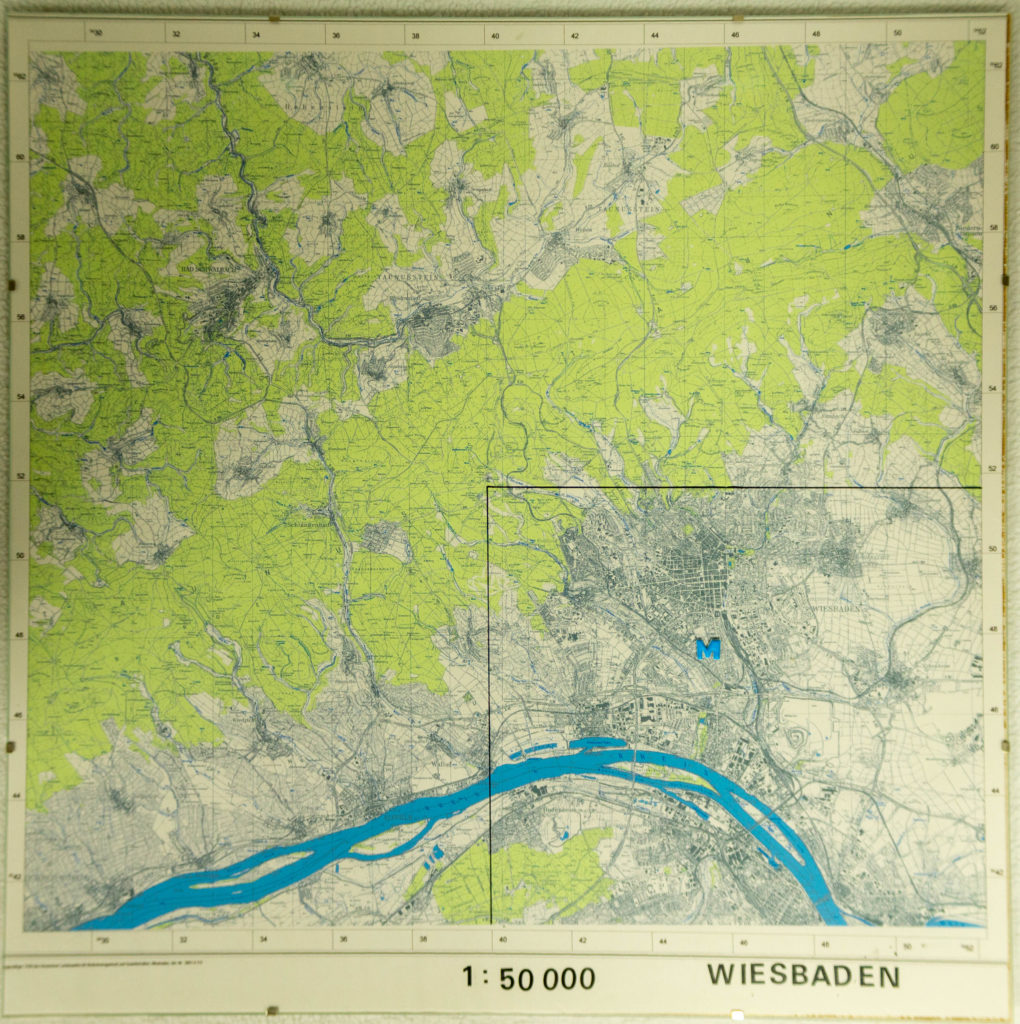
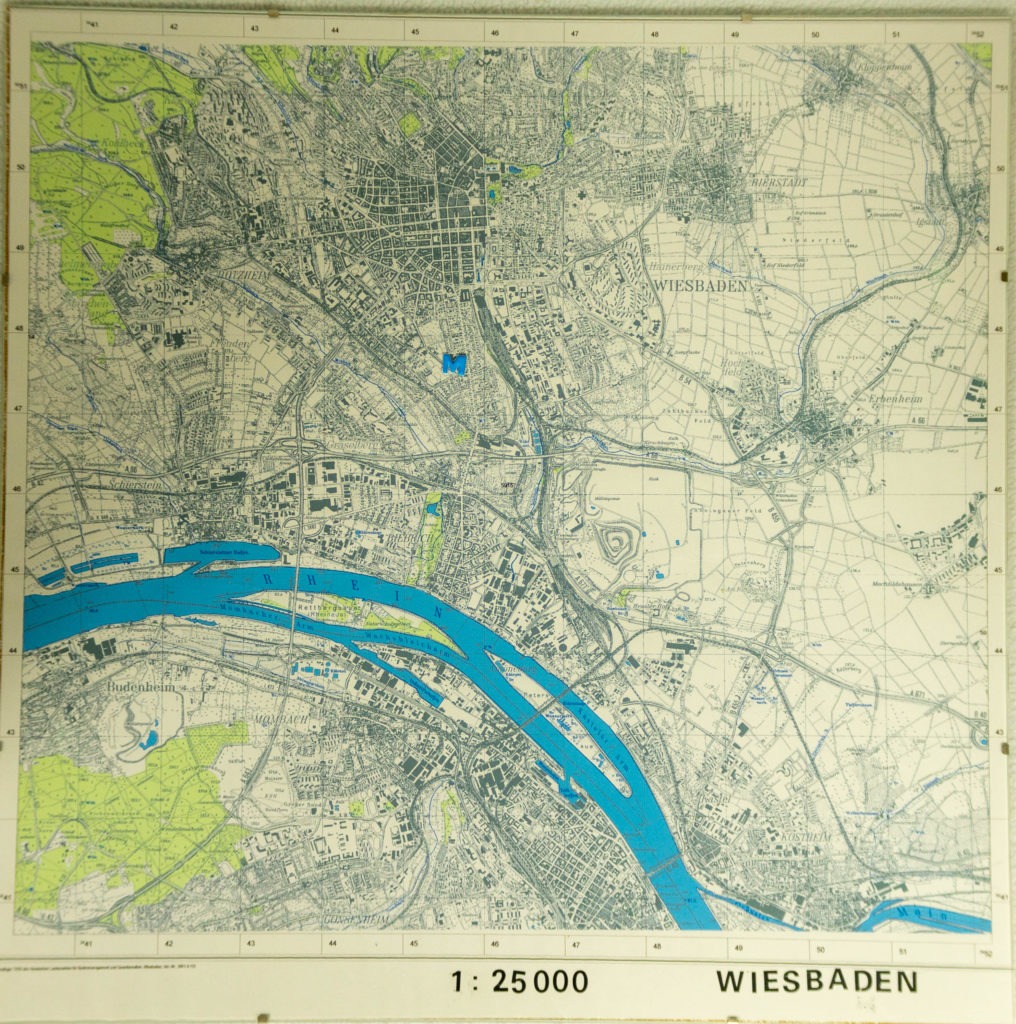
In der Mathothek gibt es zwei sogenannte „Messtischblätter“, das sind landesamtliche Grundkarten im Maßstab 1:25.000 bzw. 1:50.000 mit der hessischen Landeshauptstadt Wiesbaden:
Bei der Projektion kleinerer Ausschnitte der kugelförmigen Erdoberfläche ist das meistens auch kein Problem. Je größer der Maßstab, desto geringer ist der Unterschied zwischen der gewölbten Oberfläche und der ebenen Abbildung. Aber es bleibt ein grundsätzliches Problem: Aus mathematischen Gründen ist die exakte Übertragung der Oberfläche einer Kugel oder auch nur von Ausschnitten in eine ebene Fläche nicht ohne Verzerrungen möglich: Die Abstände oder die Winkel oder die Flächengrößen stimmen nicht überein. Um trotzdem brauchbare Karten zu konstruieren, wurden verschiedene Methoden entwickelt. So beispielsweise die Mercatorprojektion, bei der die Winkel auf der ebenen Karte mit den entsprechenden Winkeln auf der Kugel übereinstimmen. Solche winkeltreue Karten waren verständlicherweise für die Seefahrt besonders wichtig.
Den Vorgang einer möglichen Projektion von einer Kugeloberfläche auf eine ebene Fläche kann man in der Mathothek sehr anschaulich erfahren, und zwar mithilfe eines weiteren Experiments, das aus einer Taschenlampe und einem mithilfe eines mit einem 3D-Drucker hergestellten kugelförmigen Objekts besteht:
Benutzt man jetzt die punktuelle Lichtquelle der Taschenlampe und hält sie so, dass sie sich an der Stelle des fehlenden obersten Punktes der Kugel befindet, so wird auf der ebenen Tischfläche folgendes Bild projiziert:
Wie man bei diesem Experiment unmittelbar sieht, werden hier rechte Winkel auf der Kugel auch als rechte Winkel bei der Projektion in der Ebene abgebildet. Aber diese Art der Projektion ist offensichtlich nicht längentreu.
Die getreueste kartographische Abbildung der Oberfläche der Erdkugel ist natürlich der Globus, auch wenn er wegen des sehr kleinen Maßstabs nur sehr begrenzt Informationen aufnehmen kann.
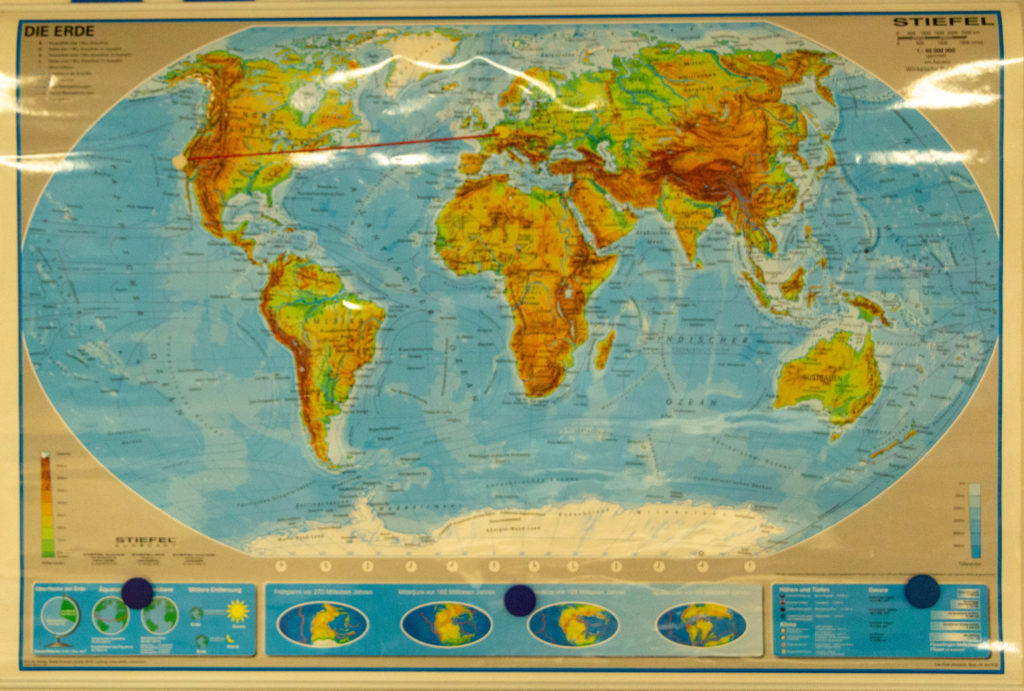
Mithilfe dieses physischen Modells der Erde im Maßstab 1:42.000.000 und einer Weltkarte im Maßstab 1:40.000.000 lassen sich viele Probleme der Verzerrung überzeugend erfahren, z.B. auch im Hinblick auf die kürzeste Verbindung zweier Städte. Angeregt durch das Buch „Wie man in eine Seifenblase schlüpft“ von A. Beutelspacher entstand hier ein Staunen lassendes Exponat: Wir suchen auf der Weltkarte und dem Globus die beiden Städte Frankfurt am Main und Los Angeles auf und verbinden sie mit einem roten Faden.
Auf der Weltkarte:
und auf dem Globus:
Schon ein erster Blick zeigt uns, dass die beiden Ergebnisse sich ganz offensichtlich widersprechen: Auf der Weltkarte führt der „kürzeste Weg“ weit südlich an der Spitze Grönlands vorbei. Auf dem Globus dagegen führt die Route ein gutes Stück über den Süden Grönlands. Eine der beiden Konstruktionen der kürzesten Route muss falsch sein. Als einzige Auflösung des Widerspruchs bleibt, die gesuchte kürzeste Route auf der Weltkarte ist nicht identisch mit der geraden Verbindung der beiden Punkte auf dieser. Da wir beim Globus – dem getreuen Abbild der Erde – sicher sein können, mit dem gespannten Faden den kürzesten Weg gefunden zu haben, muss unsere kürzeste Verbindung auf der Weltkarte falsch sein, kann also in der Projektion nicht der geraden Strecke zwischen den beiden Punkten entsprechen.
Auf dem Globus ist die kürzeste Verbindung zweier Punkte identisch mit deren geraden Verbindung, also wie wir es auch von der Ebene gewohnt sind. Diese Strecke verbindet die beiden Punkte auf einem Großkreis, das sind die Geraden auf einer Kugel. Großkreise sind alle jene Kreise auf einer Kugel, die den Kugelmittelpunkt zum Kreismittelpunkt haben. Daher „rutscht“ bei Spannung der rote Faden auf dem gewölbten Globus auf einen Abschnitt eines Großkreises, wo die Spannung des Fadens minimal ist. Damit zeigt der rote Faden jenen Abschnitt des Großkreises durch die beiden Städte, der ihrer kürzesten Verbindung entspricht. Die beiden Städte und der Erdmittelpunkt bestimmen eindeutig einen Großkreis.
Betrachten wir nun einmal den dreieckigen Flächenausschnitt der Erdoberfläche, der vom Äquator, dem 0. und dem 90. Längengrad östlicher Länge begrenzt wird:
Wir stellen natürlich fest, dass diese Fläche auf der Kugeloberfläche ein gleichseitiges Dreieck ist, bei dem alle drei Winkel gleich 90° groß sind – was uns mehr als erstaunt. Aus der bisherigen Geometrie wussten wir doch, dass bei jedem gleichseitigen Dreieck die Summe der Innenwinkel immer 180° beträgt, dass die Summe der drei Innenwinkel immer kleiner oder gleich 180° beträgt.
Kommen wir auf die Idee, auf einer Kugel einen Kreis zu zeichnen, so werden wir erneut ins Staunen versetzt. Als Beispiel nehmen wir den südlichen Polarkreis, den wir rot einfärben. Die Länge des Umfangs des Polarkreises ist offensichtlich kleiner als die gewohnte Formel „Kreisdurchmesser mal π“ in der ebenen Geometrie besagt. Diesen ersten Eindruck können wir aber anschaulich jedoch nachvollziehen. Die Länge von 5.232 km des Durchmessers eines Polarkreises der Erde ergibt sich durch die Verdopplung des Abstands des Südpols vom südlichen Polarkreis, d.h. 2⋅2.616 km. Nach der aus der ebenen Geometrie vertrauten Formel U=π⋅d ergibt sich für die die Länge des Polarkreises 8.214,24 km. Die tatsächliche Länge der Polarkreise beträgt aber jeweils nur 7.998,15 km. Wichtiger Hinweis: Solltest Du Dich eines Tages in einer Dir unbekannten Welt wiederfinden, so zeichne einen Kreis, miss dessen Umfang und Durchmesser und teste die euklidische Kreisumfangsformel. Ist das Ergebnis kleiner als berechnet, so befindest Du Dich auf einer Kugel oder elliptischen Fläche, ist es größer, dann auf einer hyperbolischen Fläche. Nur im dritten Fall kannst Du Deine vertraute euklidische Geometrie sicher benutzen.
Auch das folgende Objekt – ein einfacher Jonglierball aus roten, gelben, blauen und grünen Leder-„Zweiecken“ – in der Mathothek lässt den „Geometer der Ebene“ staunen: Gibt es auf einer Kugel auch Vielecke mit weniger als drei Ecken? Bisher selbstverständlich unmöglich. Dazu kommt die Erkenntnis, dass die Innenwinkelsummen in solchen Zweiecken größer als 0° und kleiner als 720° sein können.
Durch die aufgeklebte blaue Gerade (blauer Großkreis) entstehen aus den vier Zweiecken dann acht gleichseitige (sphärische) Dreiecke. Bei jedem dieser Dreiecke beträgt dann offensichtlich die Summe aller Innenwinkel 3⋅90°=270°.
Um die Besonderheiten der Geometrie auf der Kugel anschaulicher zu machen, gibt es zwei weitere einfache Objekte in der Mathothek. Hier geht es besonders um Beziehungen von Punkten und Geraden, „schneiden“ und „liegen auf“, aber auch um Parallelität und Vielecke auf der Kugel:
Diejenige Geometrie, die auf einer Kugeloberfläche gilt, bezeichnet man als elliptische Geometrie. Sie unterscheidet sich – wie wir schon gesehen haben, wesentlich von der euklidischen Geometrie der Ebene. So unterscheiden sich die Geraden in einer Ebene von den „Geraden“ auf der Kugel, letztere sind die Großkreise auf der Kugel, d.h. zwei Punkte einer Kugeloberfläche liegen auf ein und derselben Geraden, wenn sie in derselben Ebene wie der Kugelmittelpunkt liegen. Im anfassbaren Beispiel stellen die dunkelblauen Punkte Antipoden dar. Der hellblaue Punkt liegt auf dem Großkreis mit dem dunkelblauen, der Großkreis ist also die Verbindungsgerade der beiden Punkte.
Zwei Punkte, die auf der Kugel Antipoden sind, also auf einer Geraden mit dem Kugelmittelpunkt der Kugel liegen, werden als gleich angesehen.
Daraus ergibt sich, dass es auf der Kugel keine Parallelen geben kann, weil irgend zwei Großkreise immer einen Punkt (und seinen Antipoden) als Punkt gemeinsam haben, dass es auch Zweiecke gibt und sogar Dreiecke mit einer Innenwinkelsumme, die größer als 180° ist.
Zu den nicht-euklidischen Geometrien, aber auch der Geschichte und Gültigkeit des Parallelenaxioms gibt es in der Mathothek weitere Objekte und Artikel, z.B. gehäkelte Veranschaulichungen von Modellen zur elliptischen und hyperbolischen Geometrie:
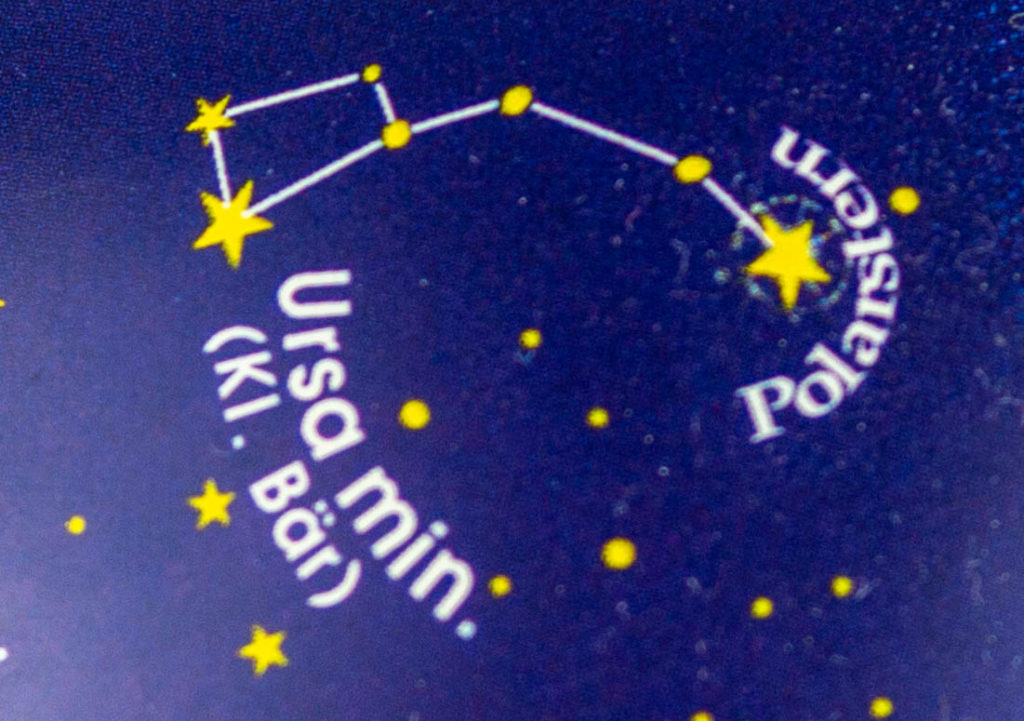
Noch problematischer als die Projektion einer Kugel auf eine Ebene ist die Projektion der Sternenwelt auf eine Kugel, also die Projektion des gesamten Raums auf die Oberfläche einer Kugel. Dabei besteht das Problem nicht einmal in der Menge der darzustellenden Objekte, sondern in der Darstellung von deren Positionen, Größen- und Längenverhältnissen. Auch auf einem sehr großen Sternenglobus würde die Länge des Abstands zweier Fixsterne – genauso wie auf dem kleinen Sternenglobus in der Mathothek – verzerrt sein, wenn nicht beide Himmelskörper gleich weit von der Erde sind. Aber die Darstellung des Sternenhimmels diente zur Orientierung auf der Erde, z.B. in der Seefahrt oder magischen Vorstellungen und entsprang dem ewigen Wunsch der Menschen, auch im Überirdischen, feste Muster zu erkennen. So kann auch heute noch eine Sternenkarte oder ein Sternenglobus uns dabei helfen, bestimmte Sterne und Sternbilder in einer klaren Nacht zu finden. Auf der Nordhalbkugel spielte der Polarstern eine sehr wichtige Rolle als Orientierungshilfe.
Durch die Projektion unserer Ansicht des „Sterngewölbes“ auf zweidimensionale Sternkarten wird zwar auch wieder einiges verzerrt, aber auch zusätzliche Informationen, wie z.B. den Anblick zu bestimmten Zeitpunkten usw. möglich.
Zwei drehbare Sternkarten in der Mathothek:
Gut nachzuvollziehen ist die Darstellung des Erdtrabanten, des Mondes durch Beibehaltung seiner Kugelgestalt. So fällt es uns recht leicht bei der Beobachtung des Mondes als helle Kreisscheibe am Nachthimmel, ihn uns als Kugel vorzustellen. Dabei lieferte erst die moderne Weltraumforschung die Informationen über das Aussehen seiner erdabgewandten Hälfte.
Mit dem Mondglobus werden auch die Mondphasen und andere Fakten leichter vorstellbar. Die Entstehung von Neumond, zunehmendem, Halbmond, Vollmond und abnehmendem Mond werden erst durch die Kugelgestalt des Erdbegleiters logisch erfassbar. Dies zeigen auch Fotos in der Ausstellung Mathematik auf Schritt und Tritt in Mainz und Wiesbaden: