In der reichhaltigen Würfelsammlung der Mathothek gibt es die verschiedensten Typen von Objekten, die zu interessanten und vielfältigen Wahrscheinlichkeitsexperimenten benutzt werden können.
Eine große Gruppe dieser gesammelten Würfel kann aufgrund ihrer Beschaffenheit und ihrer Form leicht in ein mathematisches Wahrscheinlichkeitsexperiment umgesetzt werden. Beispiele sind solche Würfel, die aus einheitlichem Material bestehen und von solcher regelmäßigen geometrischen Form sind, dass alle möglichen Ausgänge gleich wahrscheinlich sind. Das ist beispielsweise bei allen Würfeln möglich, die eine der fünf platonischen Körperformen besitzen. Hierher gehört natürlich auch der allbekannte kubische Würfel oder das Hexaeder:
Es gibt aber in dieser Würfelsammlung auch eine Menge „Würfel“, deren Ausgänge bei einem Wurf zwar gut festzustellen sind, aber es sehr schwierig ist, die einzelnen Wahrscheinlichkeiten zu bestimmen. Hier sind einige Beispiele:
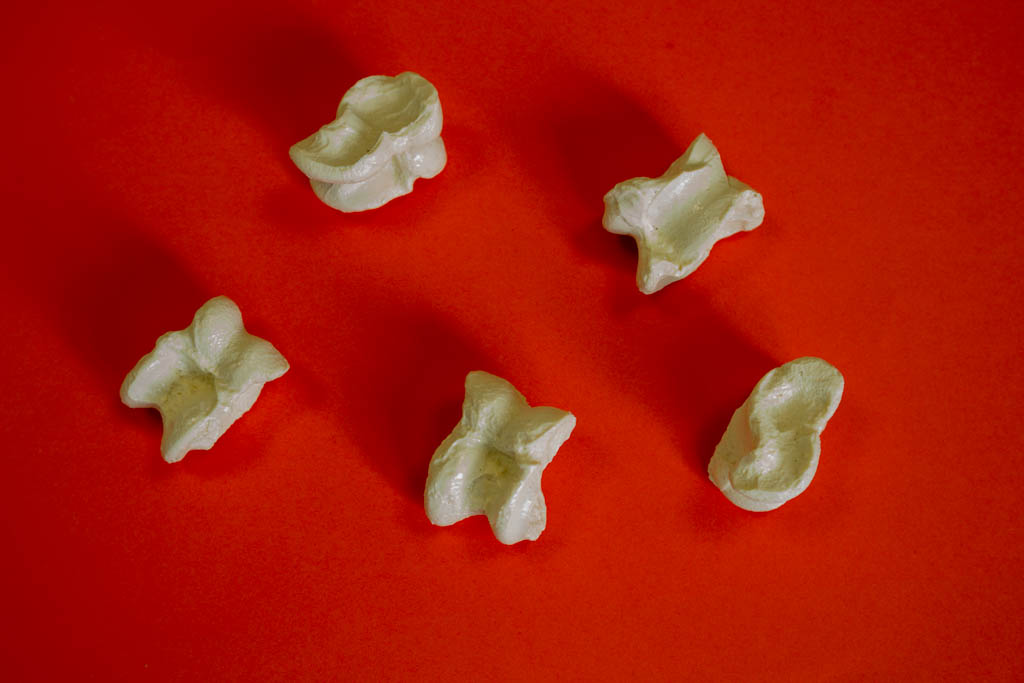
Inzwischen besitzt die Mathothek ein weiteres Set von solchen Würfeln. Es handelt sich dabei um fünf Würfel aus Kunststoff, die echten Astragalen nachempfunden sind. Astragale sind Sprunggelenksknochen von Paarhufern, wie beispielsweise von Schafen, Ziegen oder Rindern.
Astragale besitzen vier ungleiche Seiten, die man leicht unterscheiden kann und die ohne weitere Bearbeitung als Würfel verwendet werden konnten. Funde aus dem alten Orient zeigen, wie verbreitet diese Würfel bereits in prähistorischer Zeit waren. In ländlichen Gebieten Griechenlands und der Türkei wird heute noch immer mit Astragalen gespielt, ebenso in den islamischen Ländern des Vorderen Orients und Zentralasiens, aber auch in Frankreich.
Es gibt viele Möglichkeiten und Regeln, mit Astragalen zu spielen in Form von Geschicklichkeits-, Bewegungs- und Ratespiele, Würfelspiele natürlich und Mischformen. Astragale wurden in Griechenland und Kleinasien auch als Orakel benutzt.
Die Spielregeln, die dem Objekt beiliegen, wurden uns durch die Römer überliefert:
Eine beliebige Anzahl von Spielern bestimmt zunächst den Einsatz, der in die Mitte platziert wird. Reihum, im Uhrzeigersinn, würfeln die Spieler mit vier Knöchelchen. Die erreichten Punkte werden jeweils notiert. Nach 10 Runden oder einem Venuswurf ist das Spiel beendet. Gewonnen hat der Spieler mit der höchsten Punktzahl. Bei gleicher Punktzahl wird der Einsatz geteilt.
Zählweise:
- Schmalseite mit Mulde (Hund) 1 Punkt
- Breitseite ohne Mulde (Feuer) 3 Punkte
- Breitseite mit Mulde (Adler) 4 Punkte
- Schmalseite ohne Mulde (Prinz) 6 Punkte
Besondere Würfe:
- Venuswurf: Alle vier möglichen Seiten (Hund, Feuer, Adler und Prinz) auf einmal. Der Spieler gewinnt sofort das Spiel und bekommt den Einsatz.
- Nur Hunde: Geringste Punktzahl, der Spieler scheidet sofort aus.
- Viermal Feuer, Adler oder Prinz:Der Wert der Punkte wird mal vier genommen und es gibt noch 20 Extrapunkte dazu. Werden drei gleiche Seiten gewürfelt, so gibt es 10 Extrapunkte und bei zwei gleichen Seiten gibt es fünf Extrapunkte.
Drei Beispiele:
Es wurde zweimal Adler, ein Hund und ein Prinz geworfen. Das ergibt insgesamt 4+4+1+6+5=20 Punkte.
Es wurde dreimal Hund und einmal Adler geworfen. Das gibt 1+1+1+4+10(Extrapunkte)=17 Punkte.
Es wurde viermal Feuer geworfen. Das ergibt (3+3+3+3)⋅4+20(Extrapunkte)=68 Punkte.
Das Meisterwurfspiel war sehr verbreitet und war etwas einfacher:
Jeder Spieler würfelte mit einem seiner bis zu fünf Knöchelchen. Wer die höchste Punktzahl hatte, durfte die Knöchelchen der Mitspieler an sich nehmen. Gespielt wurde so lange, bis ein Spieler kein Knöchelchen mehr hatte.
Das bekannteste und am meisten verbreitete Geschicklichkeitsspiel, das mit fünf Astragalen gespielt wird, nannten die Griechen pentelitha (Fünfsteinspiel). Es wird auch heute noch in Griechenland, der Türkei und in England gespielt, aber oft mit Steinchen statt der Knöchelchen. Nach römischer Überlieferung wurden die fünf Astragale in die Luft geworfen und mussten dann auf dem Handrücken aufgefangen werden. Die heruntergefallenen mussten aufgenommen werden, ohne dass die auf dem Handrücken liegenden herabfielen. Schon in der Antike wurden das Fünfsteinspiel hauptsächlich von Mädchen gespielt.
Ein einfaches Glücksspiel mit den Astragalen war ein ganz einfaches Ratespiel mit zwei Spielern. Dabei steckte der eine verdeckt Astragale in eine Hand und der andere musste raten, ob die Anzahl gerade oder ungerade ist.
Während bei diesem Gerade-ungerade-Spiel die Chancen gleich groß sind, da es nur zwei Möglichkeiten, gerade oder ungerade, gibt. Ist es ein faires Spiel. Die besonderen Objekte spielen hier keine Rolle.
Anders ist das, wenn die besondere Beschaffenheit der „Würfel“ wesentlich ist. Der Astragal-Würfel hat eine charakteristische Form mit vier gut zu unterscheidenden Seiten:
- eine kräftig gewölbte Breitseite, die Aristoteles Bauch genannt hat
- eine Breitseite mit einer tiefen Höhlung, die er Rücken genannt hat
- eine relativ flache Schmalseite, die von den Griechen Kos genannt wurde
- eine s-förmig gekehlte Schmalseite mit einem schnabelartigen spitzen Fortsatz, die Chios genannt wurde
Wirft man den Astragal auf eine geeignete ebene Fläche, so bleibt er immer auf einer der vier Seiten liegen. Auf den beiden übrigen Seiten mit den hornartigen Fortsetzungen findet er keinen stabilen Halt. Ein Astragal unterscheidet sich also einerseits dadurch, dass es nur vier mögliche Ausgänge gibt, im Gegensatz zu sechs Möglichkeiten bei einem üblichen kubischen Würfel. Aber auch die Wahrscheinlichkeiten der vier Ausgänge sind nicht gleich. Wegen der Symmetrie des kubischen Würfels sind bei ihm alle sechs Ausgänge gleich wahrscheinlich, nämlich 1/6. Die Bestimmung der Wahrscheinlichkeiten der vier möglichen Ausgänge beim Astragal ist so einfach nicht zu ermitteln. Die Griechen haben den vier Seiten, die beim Würfeln mit einem Astragal auftreten können, Punkte zugeordnet, die nicht ihre Wahrscheinlichkeiten widerspiegeln. Danach gibt es für die Schmalseiten Kos 1 Punkt und 6 Punkte für Chios, für die Breitseiten 3 Punkte für Rücken und 4 Punkte für Bauch. (Die Punkte 2 und 5 treten nicht auf.) Damit sind die Zahlenwerte der Seiten eines Astragals wie die Augen beim kubischen Würfel so angeordnet, dass die gegenüberliegenden Seiten immer die Summe sieben ergeben. Die Sieben ist bis heute eine der magischsten Zahlen!
Wie sieht es nun aber mit der tatsächlichen Wahrscheinlichkeitsverteilung aus?
Um hier eine Antwort zu finden, müssen wir das schwache Gesetz der großen Zahl bemühen. Das intuitive Erfassen dieses mathematischen Gesetzes als empirisches Gesetz der großen Zahl ist kein Problem. Man würfelt möglichst eine große Anzahl Male hintereinander, notiert sich die jeweiligen Ergebnisse. Am Ende zählt man
- die Zahl der Würfe insgesamt: n
- die absolute Häufigkeit des interessierenden Ereignisses: z.B. H(Rücken)
- durch Division der absoluten Häufigkeit durch die Anzahl aller Würfe erhält man die relative Häufigkeit des Ereignisses: hn(Rücken)=H(Rücken)/n
Durch Untersuchung der relativen Häufigkeiten wurde beobachtet, dass der Astragal in 80 % aller Fälle auf einer der beiden Breitseiten liegen bleibt und nur in 20 % auf einer der beiden Schmalseiten. Dabei sind die jeweiligen relativen Häufigkeiten weder für die beiden Breitseiten noch für die Schmalseiten gleich.
Erfahrung und Intuition zeigen dann, dass bei immer größeren Versuchsreihen von unabhängigen Wiederholungen des gleichen Versuchs sich die relativen Häufigkeiten eines Ereignisses immer mehr stabilisieren. Das schwache Gesetz der großen Zahl sagt nun, dass sich die relative Häufigkeit eines Ereignisses, wenn man immer längere Reihen des Experiments durchführt, mit immer größerer Genauigkeit an die Wahrscheinlichkeit dieses Ereignisses annähert.
Daher können wir aufgrund der obigen Mitteilung annehmen, dass die Wahrscheinlichkeit für „Breitseite“ pB=4/5 und für „Schmalseite“ pS=1/5. Um Näherungswerte für die Wahrscheinlichkeiten jeder der vier einzelnen Seiten zu bekommen, bist Du gerne in die Mathothek eingeladen, um zu Würfeln.