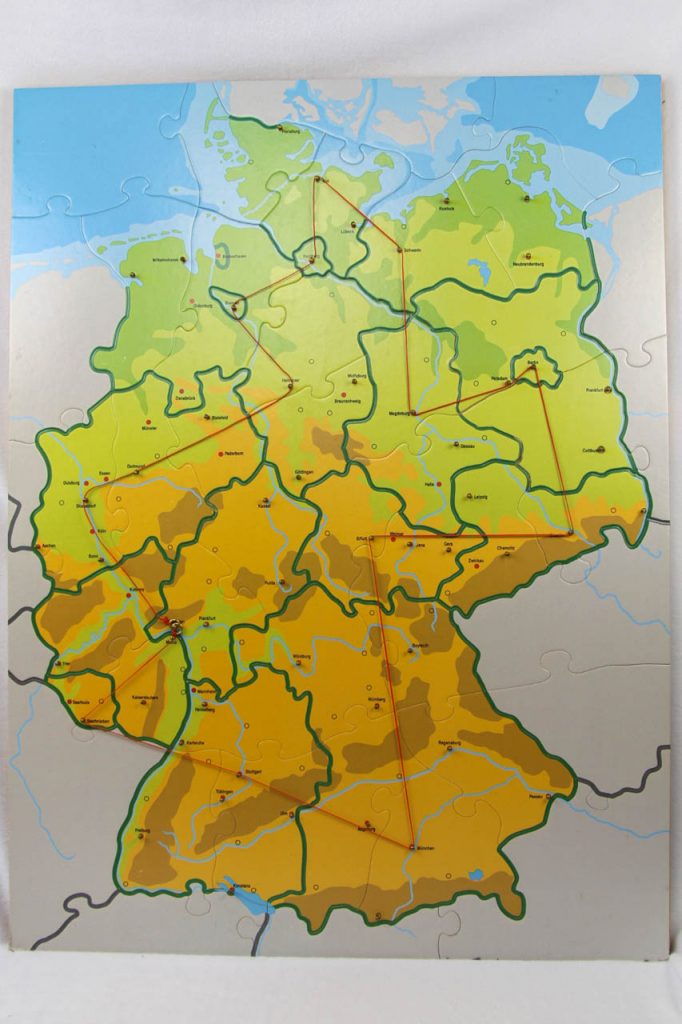
In dem Artikel „Kürzeste Rundreise durch die 16 Hauptstädte“ sehen wir einen hamiltonschen Kreis:
Der zugrundeliegende Graph ist nicht vollständig gezeichnet. Die Knoten (oder Ecken) sind die 16 Landeshauptstädte der BRD. Die 16·15 Kanten – die jede der 16 Städte mit jeder der anderen 15 Städte verbinden – sind wegen der Unübersichtlichkeit nicht eingezeichnet. Es handelt sich hier um einen vollständigen Graphen. Ein Graph heißt vollständig, wenn alle Ecken untereinander durch Kanten verbunden sind. Die Lösung oben auf dem Bild ist ein hamiltonscher Kreis: Diese Auswahl von Kanten verbindet alle Knoten des Graphen genau einmal zu einem geschlossenen Pfad, also einer „Rundreise“. In jedem vollständigen Graphen lässt sich so ein geschlossener Pfad finden, der alle Knoten genau einmal enthält. Dass es hier um einen besonderen hamiltonschen Kreis geht – kürzeste Rundreise – hängt damit zusammen, dass es sich hier um einen bewerteten Graphen handelt, weil jede Kante einen Wert zugeordnet bekommt, hier die Entfernung der beiden Städte (=Knoten).

Auch die beliebten „Sterne“ sind vollständige Graphen und besitzen demnach immer einen hamiltonschen Kreis. Ein solcher hamiltonscher Kreis findet sich immer, indem man einfach den Pfad bei einer Ecke beginnt nach rechts oder links zur nächsten Ecke geht, bis man am Anfang wieder angekommen ist. Aber nicht immer ist der Graph ein geschlossener Kreis. Die folgenden „Sterne“ besitzen nicht nur einen Hamilton’schen, sondern auch einen Euler’schen Kreis. Man kann also alle Knoten durch einen geschlossenen Pfad genau einmal verbinden und alle Kanten genau einmal begehen, d.h. den Graphen „in einem Zug zeichnen“.
An zwei platonischen Körpern – Tetraeder und Hexaeder – ist jeweils ein hamiltonscher Kreis markiert worden: Die rosa Klebebänder verbinden die vier bzw. acht Ecken durch einen hamiltonschen Kreis.
Zeichnet man die geplätteten Graphen der fünf platonischen Körper, so lassen sich für jeden der fünf besonderen Körper ein hamiltonscher Kreis aufzeigen.
Mit dem wunderbaren „Mathmaker“-Baukasten aus der Mathothek lässt sich ein hamiltonscher Kreis eines Oktaederstumpfes aus den entsprechenden mit Magneten versehenen hölzernen Bauteilen bauen:

Der entsprechende archimedische Körper – Oktaederstumpf – hängt in der Mathothek von der Decke und der obige hamiltonsche Kreis ist auf ihm rosa markiert.

Warum heißt es aber in der Überschrift „Rundreise durch 20 Städte“? Nun das hat etwas mit dem Namensgeber zu tun. Im Jahr 1857 erfand der irische Mathematiker Sir William Rowan Hamilton ein Spiel, das er „Traveller’s Dodecahedron“ und auch „A Voyage Round The World“ nannte. Es bestand aus einem hölzernen Dodekaeder, dessen 20 Ecken mit 20 Städten der Erde assoziiert waren. Die Aufgabe bestand in der Suche eines Reiseweges, der genau einmal durch jede der 20 Städte und am Ende wieder in die Ausgangsstadt führte, also darin einen „hamiltonschen Kreis“ auf einem Dodekaeder zu finden.
Bei aller Ähnlichkeit zum Euler’schen Kreis, dessen Nachweis recht einfach ist, ist der beim Hamilton’schen Kreis wesentlich aufwändiger.