Ein weit verbreiteter Erklärungsversuch für die Sonderstellung der Sieben in vielen Kulturen und Zeiten ist das Vorhandensein der sieben Öffnungen der menschlichen Wahrnehmungsorgane im menschlichen Kopf: zwei Ohren, zwei Augen, zwei Nasenlöcher und ein Mund. Die volkstümliche Auffassung der sieben Sinne (Sehen, Hören, Riechen, Schmecken, Tasten, Orientierung und Gleichgewicht) korrespondiert damit. Auch hier haben wir die Sieben als Summe von fünf (Sehen, Hören, Riechen, Schmecken und Tasten) und zwei (Orientierung und Gleichgewicht). Zu den Auftritten der Sieben in der Biologie gehört auch die Zahl der Zähne (7 je Gebisshälfte, oben und unten, sofern die Weisheitszähne – noch – nicht angelegt sind).
Auf die fünf Kopf-Öffnungen soll die kleine Büste des Komponisten Verdi hinweisen:
Diese kleine, unscheinbare Pflanze ist nicht so häufig zu finden. Wenn sie aber blüht, ist sie sehr leicht zu erkennen. Der Grund dafür liegt in der ungewöhnlichen Siebenzahl ihrer Blütenblätter. Die am häufigsten zu findende Anzahl bei den Blütenblättern einer Blume dürfte die Fünf sein, egal ob die Blüte dreh- oder achsensymmetrisch ist. In der Mathothek gibt es eine Abbildung des Siebensterns:
Ein durchaus sympathischer Bewohner unserer Breiten ist der Siebenschläfer, aber nicht der Lostag am 27. Juni, sondern das pelzige Nagetier. Seinen Namen „Siebenschläfer“ hat dieses Tier, weil es von Oktober bis April seinen Winterschlaf hält und dann nur von seinen Fettreserven zehrt.
In der Biologie und der Medizin unterscheidet man beim Menschen sieben Drüsensysteme:
- Zirbeldrüse (Epiphyse)
- Hirnanhangdrüse (Hypophyse)
- Schilddrüse und Nebenschilddrüsen
- Thymus
- Nebenniere
- Pankreas (Bauchspeicheldrüse)
- Ovar bzw. Hoden (Geschlechtsdrüsen).
In der Chemie hat die Sieben ebenfalls mehrere besondere Auftritte. Ein wichtiger Teil der Chemie befasst sich mit Kristallen, den regelmäßigen geometrischen Vorkommen der natürlichen Verbindungen der Elemente.
Aufgrund der regelmäßigen symmetrischen Struktur der Kristalle lassen die sich einem der sieben Kristallsysteme zuordnen. Darauf soll das oben abgebildete kleine Kästchen mit Kristallbeispielen hinweisen.
Kubisches System:
In der Mathothek gibt es sowohl eine stattliche Mineraliensammlung als auch 15 Glasmodelle, die die wichtigsten geometrischen Formen von Kristallen verkörpern. Diese interessanten Glaskörper mit ihren Symmetrien gehören mit zu den ältesten Exponaten der Mathothek, sie entstanden vor über Hundert Jahren.
Tetragonales Kristallsystem
Hexagonales Kristallsystem
Trigonales Kristallsystem
Orthorhombisches Kristallsystem
Monoklines Kristallsystem
Triklines Kristallsystem
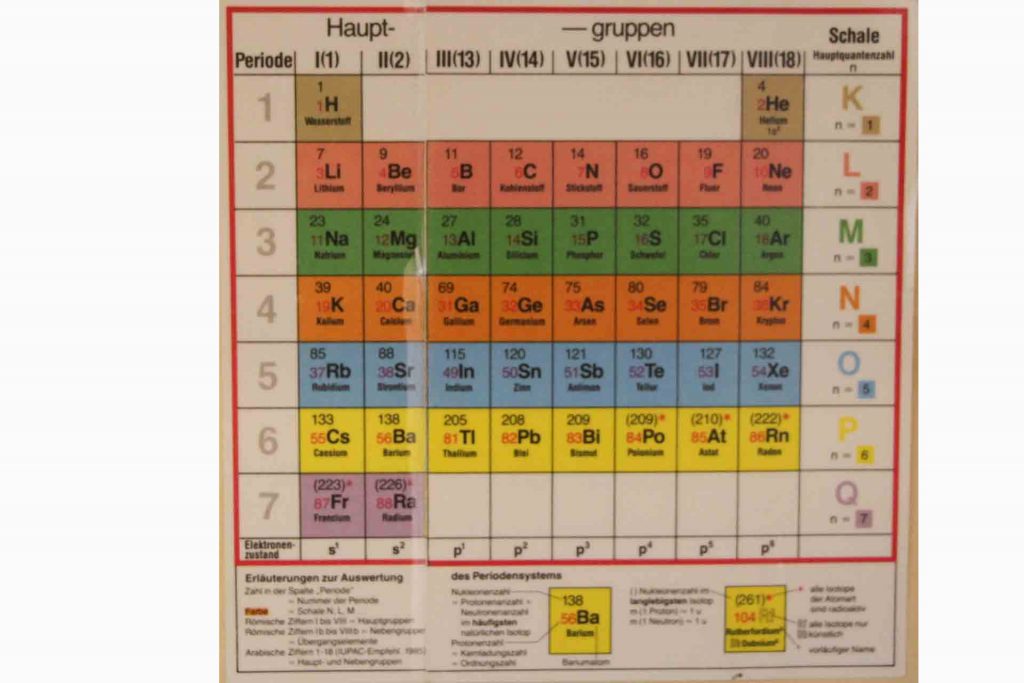
In der Chemie findet man die Sieben auch in der grundlegenden und systematischen Zusammenstellung der Elemente, dem Periodensystem. Man unterscheidet im Periodensystem acht Hauptgruppen mit insgesamt sieben Perioden.
Der pH-Wert in der Chemie gibt an, wie sauer oder basisch ein Stoff ist. Dabei zeigt der pH-Wert 7 an, dass der Stoff weder sauer, noch basisch ist, sondern neutral.
Auf den ersten Blick scheint es in der Chemie so, als spielte hier beim naturwissenschaftlichen Denken die Magie der Sieben keine Rolle und ihr Auftreten sei nur sachlich begründet. Beim genaueren Hinsehen lässt sich jedoch der Verdacht nicht ganz von der Hand weisen, dass beim Ordnen und Systematisieren die Sieben ganz willkommen war. Es wäre vielleicht bei der Einteilung der Kristallsysteme auch mit sechs Kategorien gegangen, indem man das hexagonale und das trigonale System zu einem einzigen zusammengefasst hätte. Aber natürlich ist die Einteilung in sieben Systeme vernünftig und die Sieben magisch!
Etwas Ähnliches können wir auch bei dem großen Physiker Isaak Newton beobachten. Er hat sich aber bei seiner Entscheidung für die Sieben als Anzahl der Farben des Regenbogens auf seine Vorliebe für diese magische Zahl entschieden.
Isaac Newton führte da Vincis Theorien zu Beginn des 18. Jahrhunderts fort.
Newton schickte Licht durch ein gläsernes Prisma und kam zu dem Ergebnis, dass weißes Licht durch das Glas in Farben zerlegt wird, wie bei einem Regenbogen. Er stellte auch fest, dass eine weitere Zerlegung einer Farbe nicht mehr möglich war. Diese Farben nannte Newton deshalb Spektralfarben. die er als Grundlage für seinen Farbkreis nahm. Danach sind die Farben Rot, Grün und Blau die Grundfarben, die als Summe Weiß ergeben. Schwarz gilt in der Farbenlehre von Newton als Abwesenheit von Licht.
Im Gegensatz zu vielen Zeitgenossen, setzte der Naturwissenschaftler dabei vor allem auf quantitative, mathematische Vorgehensweisen, die teilweise öffentlich nicht anerkannt wurden und auf viel Widerstand trafen. Insbesondere mit dem Schriftsteller und Dichter Johann Wolfgang von Goethe, der seine ganz eigene Theorie zur Entstehung der Farben hatte, kam es so häufiger zu Disputen.
Heutzutage hat sich jedoch die Lehre Newtons als Fundament der Farbenlehre durchgesetzt und lässt sich bequem parallel zu der des weltberühmten Dichters betrachten.
In seiner 1704 erschienen Abhandlung Opticks schreibt Newton, dass weißes Licht aus sieben Farben bestehe: Rot, Orange, Gelb, Grün, Blau, Indigo (Hellblau/Cyan) und Lila. Diese Anordnung ist natürlich auch nicht zufällig gewählt, sondern basiert auf der empfindungsmäßigen Ähnlichkeit zwischen Violett und Rot. Isaak Newton führte nur sieben Farben auf, weil er – nach eigenem Bekenntnis – ein Anhänger der Siebenzahl war, von der man seinerzeit annahm, sie regiere das Universum.
Bei zunehmendem Wind vermischen sich die Farben des klassischen Windrads mit sieben Flügeln zu faszinierenden Effekten.
Ist uns an den obigen Beispielen die bis heute nachwirkende Magie der Zahl Sieben erstaunlich vorgekommen, so ist es doch fast umwerfend, dass bei der Festlegung des neuen internationalen Systems der physikalischen Einheiten ausgerechnet 7 – tatsächlich sieben – Grundeinheiten die Basis zur Ableitung aller physikalischen Größen notwendig und ausreichend sind.
Natürlich kommt die Sieben auch in der Arithmetik, dem wesentlichen Teilgebiet der Mathematik, vor.
Die Zahl 7 ist auch unter ganz rationalen Gesichtspunkten mathematisch recht interessant. 7 ist die vierte Primzahl, d.h. nur durch 1 und sich teilbar und lässt sich durch die Summen 1+6, 2+5 und 3+4 darstellen. Dabei besteht die Gleichung 2+5=7 aus drei Primzahlen. Unter den ersten zehn natürlichen Zahlen hat die 7 eine weitere Sonderstellung bezüglich der Multiplikation und der Division: Die 7 kann weder als Produkt noch als Quotient der Zahlen 2 bis 10 dargestellt werden, d.h. ohne die 1 zu benutzen. Dagegen ist das bei den anderen neun Zahlen leicht möglich, z.B. 1=10:10, 2=10:5, 3=9:3, 4=2⋅2, 5=10:2, 6=2⋅3, 7=?, 8=2⋅4, 9=3⋅3, 10=2⋅5.
Aber man gerät auch hier sofort wieder in den Bann der Magie. Sogar die Sonderstellung der Sieben, die zuletzt angesprochene mathematische Besonderheit von 7, lässt sich mystisch deuten: Gott wurde nicht gezeugt und er hat nicht gezeugt, er war vor aller Zeit und wird auch nach aller Zeit sein. Also spiegelt die Sieben auch hier das Heilige wider.
Es gibt aber in der Mathematik noch weitere interessante Auftritte. Da ist beispielsweise die Kusszahl Sieben. Sieben gleichgroße Kreise oder Kugeln in einer Ebene ordnen sich platzsparend so an,dass immer drei sich berühren, d.h. „sich küssen“.
In einem Venn-Diagramm werden mit drei „Kreisen“ die sieben Möglichkeiten dargestellt, Schnittmengen der drei Mengen A,B und C darzustellen. A∩B={ x/ x∈A und x∈B}=Menge aller Elemente, die zur Menge A und auch zur Menge B gehören. Entsprechend gilt, dass A∩C={x∈A und x∈B} und B∩C={x∈B und x∈C} sowie A∩B∩C={x∈A und x∈B und x∈C}. Zu diesen fünf Schnittmengen kommen noch die beiden Mengen A und B. „Also haben wir wieder die Sieben“, staunt der hochbegabte Linus.
Es tritt die Zahl Sieben in der Geometrie auch auf, wenn man systematisch untersucht, wie groß die Anzahl der Möglichkeiten ist, vier kongruente Quadrate (Tetrominos) aneinanderzusetzen. Dazu gibt es in der Mathothek ein Legespiel. Es gibt die sieben Tetrominos in zwei Farben. Mit ihnen lassen sich dann weitere geometrische Formen legen.
Überraschend erscheint es, dass es in der Geometrie genau sieben Typen von Bandornamenten gibt. Hier ist die Sieben die logische Folge aus den möglichen Symmetrien. Die Fotos unten zeigen drei Beispiele für konkrete Bandornamente. In der Mathothek gibt es mehrere Exponate zu Symmetrietypen in allen drei Dimensionen.
In der Geometrie ist das regelmäßige Fünfeck mit seinem Goldenen Schnitt sehr spannend. Das Siebeneck ist mit Zirkel und Lineal konstruierbar, was der „Fürst der Mathematik“ Carl Friedrich Gauß in sehr jungen Jahren als erster bewies.
In der Mathematik ist das Auftreten der Sieben tatsächlich logisch begründet und durch keine Mystik verschleiert. Umgekehrt mag aber dieses logisch begründete Auftreten der Sieben in der Mathematik im allgemeinen Bewusstsein nicht das Besondere und die Magie der Sieben infrage zustellen, sondern eher noch verstärken. Erhält die Magie der Sieben so anscheinend noch eine Verstärkung durch eine vermeintlich logische Basis.
Das gilt auch für einige Auftritte der Sieben in den Naturwissenschaften.
Auch die Rationalität, die Exaktheit, die Naturerscheinungen und ihre Gesetze haben ihre unwiderstehliche Magie oder Faszination.