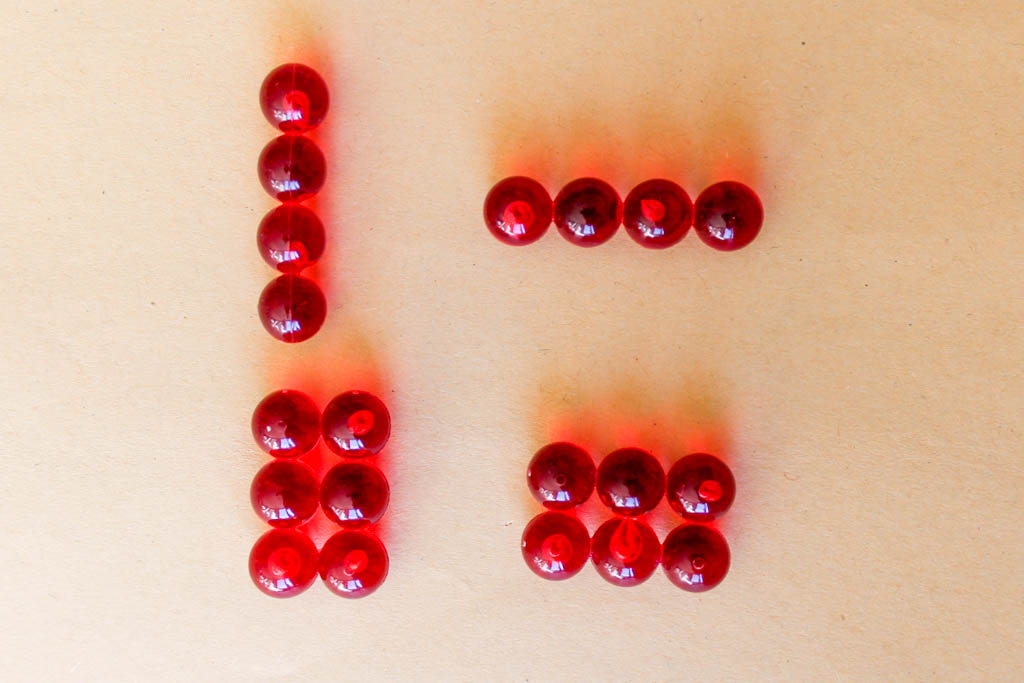In der Mathothek gibt es eine Reihe von Objekten zum Knobeln. Sie werden zur Familie der Packpuzzles gezählt. Dabei ist eines besonders faszinierend, und zwar auch für Besucher, die an sich gar keine passionierten Knobler sind. Dieses einfache Spiel ist gewissermaßen die Stammmutter zahlreicher Nachkommen aus Puzzeln, die alle den entscheidenden Trick in ihrem Erbgut bewahrt haben. Dieser Urtyp besteht nur aus zwei gleichen abgeschrägten dreiseitigen Prismen. Sie sollen zu einer Pyramide zusammengefügt werden.
Hier sind die beiden symmetrischen Teile zu sehen:
In der Regel brauchen die meisten Besucher ziemlich lange, um von der sich aufdrängenden Vorstellung loszukommen, mit Pyramide sei hier die Form „der großen Pyramide von Gizeh“ gemeint, d.h. eine vierseitige gerade Pyramide mit quadratischer Grundfläche. Mit dieser Vorstellung müssen die ersten Lösungsversuche scheitern. Wer aber erkennt, dass eine Pyramide auch aus drei Seiten und einer Grundfläche bestehen kann, der steht schon fast am Ziel. Vielleicht kommt jemand dann durch entspanntes Probieren ins Ziel. So lässt sich leicht vermuten und dann nachprüfen, dass die beiden Rechtecksflächen der beiden Teile gleich große Quadrate sind und exakt aufeinander passen. Mit dem richtigen „Dreh“ hält er dann die Lösung in den Händen. Tatsächlich ist es eine dreiseitige Pyramide, bei der die beiden Quadrate als Teile der Oberfläche keine Verwendung finden konnten und im Inneren des Körpers verschwunden sind. Eine solche sehr symmetrische Pyramide, bei der nicht nur die drei Seitenflächen, sondern auch noch die Grundseite kongruente (=deckungsgleiche) sind, nennt man ein Tetraeder, das ist einer von fünf platonischen Körpern. Diese so symmetrischen Polyeder (=Vielflächner) spielen nicht nur in der Mathematik seit alters her eine große Rolle:
Damit sieht die geforderte „Pyramide“ so aus und ist ein Tetraeder:
So können wir durch die Beschäftigung mit diesem einfachen Puzzle erkennen, wie wichtig für das Lösen eines Problems das freie und nicht unnötig Grenzen setzende Denken und Herangehen ist. Dabei müssen zuerst – spätestens beim Auftreten von Schwierigkeiten – auch die Bedingungen hinterfragt werden. Es stehen in der Mathothek auch für kleine Wettbewerbe o.ä. noch einige Objekte aus zwei gleichen Teilen zusammenfügbare Tetraeder zur Verfügung:
Bei den folgenden Objekten ist der oben erfahrene Trick immer der Schlüssel zur Lösung der gestellten Aufgabe, die jeweils durch zusätzliche Hindernisse mehr oder weniger erschwert wird.
Das erste und das zweite Beispiel bestehen jeweils aus drei Teilen und lassen sich schnell auf das Ausgangsproblem reduzieren:
Das zweite besteht aus vier Teilen und lässt sich ebenfalls auf das Ausgangsproblem zurückführen, nämlich durch das Zusammenfügen zu den zwei schon bekannten Teilen:
Auch das dritte und das vierte Beispiel, die ebenfalls jeweils aus vier Teilen bestehen, funktionieren so:
Das sechste Beispiel besteht aus fünf Teilen und funktioniert ebenfalls in zwei Schritten:
In jedem Fall hilft hier die Frage danach, welche Flächen der Teile im Inneren verschwinden müssen.
Tetraeder lassen sich auch aus bestimmten Anzahlen gleich großer Kugeln zusammensetzen. In der Mathothek gibt es ein Exponat mit den ersten fünf möglichen „tetraedrischen“ Kugelpyramiden:
Bei diesem Objekt sind die Kugeln für jeweils ein Tetraeder in der gleichen Farbe angemalt. Als weitere Hilfe sind die Kugeln nicht einzeln gegeben, sondern in logischen kurzen Reihen aneinandergefügt.
Auch bei diesem Experiment ist der Trick vom Beginn der grundlegende Schlüssel zum Zusammenbau der vier nicht nur aus einer Kugel bestehenden Tetraeder. Erst beim Bau mit mehr als vier Kugeln ist eine wichtige zusätzliche Hürde zu nehmen. Mit einem weiteren kleinen Kugelspiel soll hier eine Hilfsstellung geleistet werden:
Für eine Kugel ist die Pyramide, zwar etwas befremdlich, aber trivial. Auch das Tetraeder mit vier Kugeln ist einfach: Man setzt die beiden Zwillinge um 90° gedreht zusammen. Wie es dann weitergeht, soll an einem weiteren Objekt der Mathothek gezeigt werden. Dieses kleine „Spielzeug“ zeigt nach gelungener Lösung, auch so nebenbei, wie man einen Tetraeder in einem Würfel packen kann.
Wie man leicht beobachten kann, besteht bei diesen fünf Tetraedern auf dem grünen Tablett jeweils eine Beziehung zwischen der Anzahl der Kugeln einer Kante, der Anzahl der Kugeln auf den verschiedenen Ebenen und der Summe aller Kugeln des Tetraeders. Diese Zahlenfolgen kennt man in der Mathematik mindestens seit der griechischen Antike als Dreiecks- bzw. Tetraederzahlen.
Kantenlänge: 1 2 3 4 5 6 7 …
Dreieckszahlen: 1 3 6 10 15 21 28 …
Tetraederzahlen: 1 4 10 20 35 56 84 …
Auch das folgende Tetraeder besteht aus gleich großen Kugeln. Für seinen Aufbau aus 7 Teilen, die aus zusammengefügten Kugeln bestehen, helfen einem die bisherigen Erkenntnisse nicht sonderlich:
Trotzdem für alle Puzzle-Liebhaber: Viel Erfolg und noch mehr Spaß!
Und für alle, die Freude und Reiz bei solchen oder ähnlichen Gehirnsport haben: In der Mathothek kann man knobeln, „bis der Arzt kommt“.