Bei einer Zahlenfolge handelt es sich um eine Menge von Zahlen, die sich umkehrbar eindeutig den natürlichen Zahlen 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 usw. zuordnen lassen. Eine der interessantesten Folgen ist die nach Fibonacci benannte Folge. Dazu gibt es ein interaktives Exponat in der Mathothek:
Diese unendliche Folge besteht aus natürlichen Zahlen und beginnt mit 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, usw. Ihr Baugesetz ist klar: Die beiden ersten Folgenglieder sind 1, 1. Die Summe dieser beiden ist 2, das ist die dritte Zahl der Folge. 1+2=3 ist die vierte und 2+3=5 fünfte Zahl. Weiter geht es mit 3+5=8, 5+8=13, 8+13=21 usw. Jede Zahl der Fibonacci-Folge ist die Summe ihrer beiden Vorgänger. So lautet das Bildungsgesetz der berühmten und nicht nur in der Mathematik anzutreffenden Zahlenfolge.
Der Kaufmann und Mathematiker Fibonacci (eigentlich Leonardo von Pisa, 1170-1250) benutzte diese Zahlenfolge 1202, um das Wachstum einer Kaninchenpopulation zu beschreiben. Allerdings hat er diese nach ihm benannte Zahlenfolge nicht erfunden, sie war bereits im antiken Griechenland und Indien bekannt. Wahrscheinlich hat Fibonacci ihre Kenntnis arabischen Kaufleuten zu verdanken, so wie er durch sie auch das Dezimalsystem mit den indo-arabischen Ziffern kennengelernt hat. Von dessen großen Vorteilen er so überzeugt war, dass er es in Europa bekannt machte. In seinem berühmten Buch “Liber Abaci” stellte er auch die Frage nach der Vermehrung eines einzigen Kaninchenpaares unter ganz bestimmten Bedingungen: Ein Mann hält ein Kaninchenpaar an einem Ort, der gänzlich von einer Mauer umgeben ist. Wir wollen nun wissen, wie viele Paare von ihnen in einem Jahr gezüchtet werden können, wenn die Natur es so eingerichtet hat, dass diese Kaninchen jeden Monat ein weiteres Paar zur Welt bringen und damit im zweiten Monat nach ihrer Geburt beginnen.
In der Mathothek gibt es nun ein hübsches Exponat, das diesen Wachstumsvorgang zeigt.
In diesem Beispiel geht es um das Wachstum eines Jung-Pärchens auf acht Pärchen in sechs Monaten, davon sind drei noch nicht fortpflanzungsfähig. In Fibonaccis Aufgabe sind es im 12. Monat 144 Paare und insgesamt 377 Paare. Man sieht hier gut, wie schnell das Anwachsen der Tierpopulation erfolgt.
Wenn auch dieses Beispiel vielleicht nicht vollständig überzeugt, ist die Bedeutung der Fibonacci-Folge als ein Modell für Wachstum von großer Bedeutung. Die Fibonacci-Folge hat in der Natur bei vielen Wachstumsprozessen und Strukturen eine große Bedeutung. Aber auch in der Kunst spielen diese besonderen Zahlen der Fibonacci-Folge eine bedeutende Rolle, und zwar nicht zuletzt durch ihren Zusammenhang mit dem goldenen Schnitt.
Der sogenannte “Goldene Schnitt” beschreibt eine besondere Teilung einer Strecke oder Größe in einem bestimmten Verhältnis. Eine Strecke von A nach B wird durch den Punkt S so geteilt, dass sich die längere Teilstrecke AS(=M) zur kürzeren Teilstrecke SB(=m) so verhält wie die gesamte Strecke AB(=M+m) zur längeren Teilstrecke, also M:m=(M+m):M. Auf einem Bild des Alten Rathauses von Leipzig aus der Renaissance ist die geometrische Konstruktion der Fassade eingezeichnet.
Worin besteht nun der Zusammenhang von Fibonacci-Folge und dem Teilungsverhältnis des goldenen Schnitts? Teilt man eine Strecke, ein Rechteck oder Ähnliches im Verhältnis zweier aufeinanderfolgender Fibonacci-Zahlen, z.B.2:1, 3:2, 5:3 oder 8:5 usw., dann teilt man mehr oder weniger angenähert an den goldenen Schnitt. Das liegt daran, dass die Quotienten zweier Fibonacci-Zahlen sich mit ihrer Größe immer mehr dem Wert des goldenen Schnitts, nämlich Φ=(1+√5)/2≈1,61803398… nähern, d.h. der Grenzwert für von fn+1:fn für n→∞ ist Φ.
An der Rathausfassade lässt sich gut erkennen, dass der große Rathausturm die Fassade im rationalen Verhältnis 1:2 (Drittelregel) teilt, während sich der Teilungspunkt des goldenen Schnitts in dem etwas verschobenen großen Eingangstor befindet.
In der Mathothek gibt es mehrere Exponate, mit denen die Eigenschaften der Fibonacci-Zahlen spielerisch erfahrbar gemacht werden können. Ein Beispiel sind die “Fibonacci-Türme”:
Mit diesen roten und ockerfarbenen Holzscheibchen lassen sich Türme bauen, die den Fibonacci-Zahlen entsprechen. Zu diesem Zweck lautet die Bauvorschrift, alle Türme zu bauen, mit der Maßgabe, dass nie auf einen roten Stein ein zweiter roter Stein unmittelbar gelegt werden darf. Für ockerfarbene Steine gilt dieses Verbot nicht. Baut man nun alle möglichen Türme und ordnet sie nach Anzahl der Stockwerke, so erhält man die Fibonacci-Zahlen. Hier das Bild einer Lösung der gestellten Aufgabe. Bei dieser Anordnung der Türme sieht man auch sehr gut den Aufbau der Fibonacci-Folge: Zunähst werden auf alle acht Türme der Vorgängerreihe je ein ockerfarbener Stein gelegt, anschließend können auf die fünf Türme, die aus der Vorvorgängerreihe stammen, rote Steine gelegt werden.
Auch zwei Perlenketten sind mithilfe der Fibonacci-Folge gestaltet worden und repräsentieren so Eigenschaften dieser Folge:
Bei der ersten Kette mit hellen und dunklen Holzperlen derselben Form treten die Zahlen der Fibonacci-Folge hintereinander bis zum 10. Folgenglied (=55) auf.
Bei der zweiten Kette, die helle Holzperlen in zwei Formen und rote Trennperlen besitzt, werden die Fibonacci-Zahlen durch runde und ovale Perlen repräsentiert und die einzelnen Ergebnisse durch jeweils eine rötliche Perle getrennt. Eine runde Perle steht für eins und eine ovale Perle für zwei. Es werden nun alle Zahlen von eins bis fünf in allen möglichen Summen von Nullen und Einsen gebildet und durch entsprechende runden und ovalen Holzperlen dargestellt.
Die acht hellen Holzperlen an den Verschlussteilen haben keine besondere Funktion.
Zwei Bilder von Abschnitten der Kette sollen das Prinzip noch einmal verständlich machen. Im ersten Fall sehen wir die Darstellung der Eins mit einer Wiederholung und die beiden Möglichkeiten die Zwei darzustellen, nämlich als 1+1 oder 2, also mit zwei runden Perlen oder einer ovalen.
Im zweiten Fall (links) geht es um die Darstellung der Drei: drei runde, eine ovale und eine runde oder eine runde und eine ovale Perle, entsprechend 1+1+1, 1+2 und 2+1.
Zählt man jetzt die Anzahl der möglichen Darstellungen der Zahlen eins, zwei, drei und vier, so erhält man den Anfang der Fibonacci-Folge: 1, 1, 2, 3, 5 und 8.
Es gibt noch ein weiteres Exponat in der Mathothek, das auf demselben Prinzip fußt: Eine Menge von Ein- und Zweicentstücken dient dazu, die natürlichen Zahlen 1, 2, 3, 4, 5, … mit allen Möglichkeiten aus diesen beiden Münzen zusammenzusetzen, so wie die Holzperlen in der Kette. Natürlich kommen auch hier die Fibonacci-Zahlen als Anzahlen der jeweiligen Möglichkeiten zum Vorschein. Das ist auch bei dem Exponat mit den orangen und violetten kleinen Holzquadraten so. Die Aufgabe ist die gleiche wie bei Kette und Centstücken.
Im Zusammenhang mit dem Thema Fraktale gibt es ein interaktives Objekt, das nicht nur Wesentliches zum mathematischen Verständnis von Selbstähnlichkeit vermitteln kann, sondern auch einen Bezug zur Fibonacci-Folge besitzt:
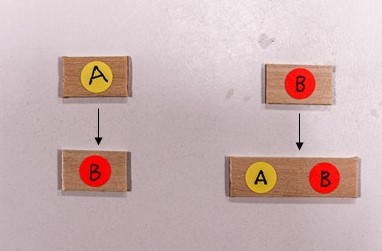
Man beginnt mit einem A und legt dann weitere Reihen nach den beiden Ersetzungsvorschriften: A→B und B→AB:
Mit diesem Vorgehen erhält man die folgenden ersten acht Reihen, bei denen man sehen kann, dass die Anzahlen der Symbole A und B in den einzelnen Reihen nach den Gesetzen der Fibonacci-Folge wachsen. Auf dem Bild (unten) sind die ersten acht Folgenglieder zu sehen. Die Beobachtung ist aber für alle unendlich vielen Reihen richtig.
Einen weiteren Auftritt haben die Fibonacci-Zahlen auf einer Treppe mit fünf Stufen:
Die fünf Stufen dieser Treppe sollen erstiegen werden, und zwar Stufe für Stufe oder auch mit Überspringen einer oder auch zweier Stufen, die aber nicht direkt hintereinander sein dürfen. Wie das Bild zeigt, geht dieser Aufstieg unter den vorgegebenen Bedingungen auf acht Arten. Um die zweite Stufe auf diese Weise zu erreichen, gibt es zwei Möglichkeiten: Man nimmt die erste und die zweite Stufe hintereinander oder man überspringt die erste. Überlegen wir jetzt, wie viele Möglichkeiten es gibt, die dritte Stufe zu erreichen. Die roten, grünen und blauen Figuren zeigen, dass es auf drei Arten möglich ist. Fünf Möglichkeiten gibt es, auf die vorgeschriebene Art und Weise die vierte Stufe zu erreichen. Also haben wir auch hier wieder die Fibonacci-Zahlen 1, 2, 3, 5 und 8. (Die eine fehlende 1 entspricht der einen Möglichkeit, vor der Treppe zu resignieren und vor ihr stehenzubleiben.)
In der Mathothek gibt es ein sehr vielseitig nutzbares Exponat mit einem sehr elementaren Aufbauprinzip. Es handelt sich um ein Pascal’sches Dreieck. Die Zahlen befinden sich auf kleinen hölzernen Rechtecken auf beiden Seiten dieser beweglichen Teilen. Dabei sind die Seiten grün bzw. gelb. Das Prinzip für das Zahlensystem des Pascal’schen Dreiecks ist ganz einfach, die Randzahlen sind alle eins und jede andere Zahl ist die Summe der beiden Zahlen, die links und rechts über ihr stehen. So einfach der Aufbau auch ist, so offenbart dieses Dreieck jede Menge Mathematik. In diesem Zahlendreieck lässt sich auch die Fibonacci-Folge finden, wie auf dem Foto zu erkennen ist.
Dabei lassen sich die Zahlen der Fibonacci-Folge im Pascal’schen Dreieck nicht unmittelbar ablesen, sondern als Summanden, deren Summe dann jeweils die nächste Fibonacci-Zahl ergibt. Als Beispiel sollen uns zunächst die orangen Zahlen in den schrägen Linien dienen. In der ersten dieser Reihen stehen zwei Einer, also 1+1=2, in der zweiten Reihe mit orangen Zahlen ergibt sich 1+5+6+1=13 und in der nächsten finden wir 1+9+28+35+15+1=89. Das ist das 11. Glied der Fibonacci-Folge. In den drei zwischen 2 und 13 liegenden grünen parallelen Reihen erhalten wir die fehlenden Zwischenglieder der Fibonacci-Folge, nämlich 1+2=3, 1+3+1=5 und 1+4+3=8. Zwischen 13 und 89 erhalten wir in den “grünen” parallelen Reihen13 und 89 finden wir die Summen 1+6+10+4=21, 1+7+15+10+1=34 und 1+8+21+20+5=55. Die beiden ersten Zahlen der Fibonacci-Folge 1 und 1 findet man in den beiden ersten “parallelen grünen Reihen”.
In einem unendlichen Pascal’schen Dreieck lassen sich auf diesem Wege auch alle Zahlen der Fibonacci-Folge auflisten.
Ein weiterer Zusammenhang der Fibonacci-Folge mit Quadraten und ähnlichen Rechtecken lässt sich mit dem folgenden Exponat der Mathothek erfahren.
Aus der folgenden Bilderreihe wird die Sache schon relativ verständlich, wenn man weiß, wie lang die Seiten der Quadrate sind. Dazu muss man nur wissen, dass die kleinsten Quadrate die Seitenlänge 1 haben. Dann erkennt man leicht, dass die anderen Quadrate alle Seitenlängen besitzen, die Fibonacci-Zahlen sind.
Die Seitenlängen der Quadrate entsprechen der Fibonacci-Folge. Durch das richtige Ansetzen des jeweils nächsten Quadrats erhält man das nächst größere Rechteck. Alle diese Rechtecke sind ähnlich, d.h. das Verhältnis der Seitenlängen ist immer dasselbe. Der Vergrößerungsprozess lässt sich, weil es unendlich viele Fibonacci-Zahlen gibt, “in alle Ewigkeit” fortsetzen.
Nimmt man nun ein solches Rechteck und zeichnet die größtmöglichen Viertelkreise in die Quadrate ein, so erhält man eine interessante Spirale, die zwar keine exakte logarithmische Spirale ist, aber doch eine gute Annäherung an die goldene Spirale.
Bei der “Suche nach dem verlorenen oder hinzukommenden kleinen Quadrat” spielen ebenfalls Fibonacci-Zahlen eine Rolle. Man suche, wo das eine Quadrat herkommt, dass das Quadrat größer macht als das Rechteck, obwohl doch beide Vierecke aus denselben Teilfiguren zusammengesetzt sind.
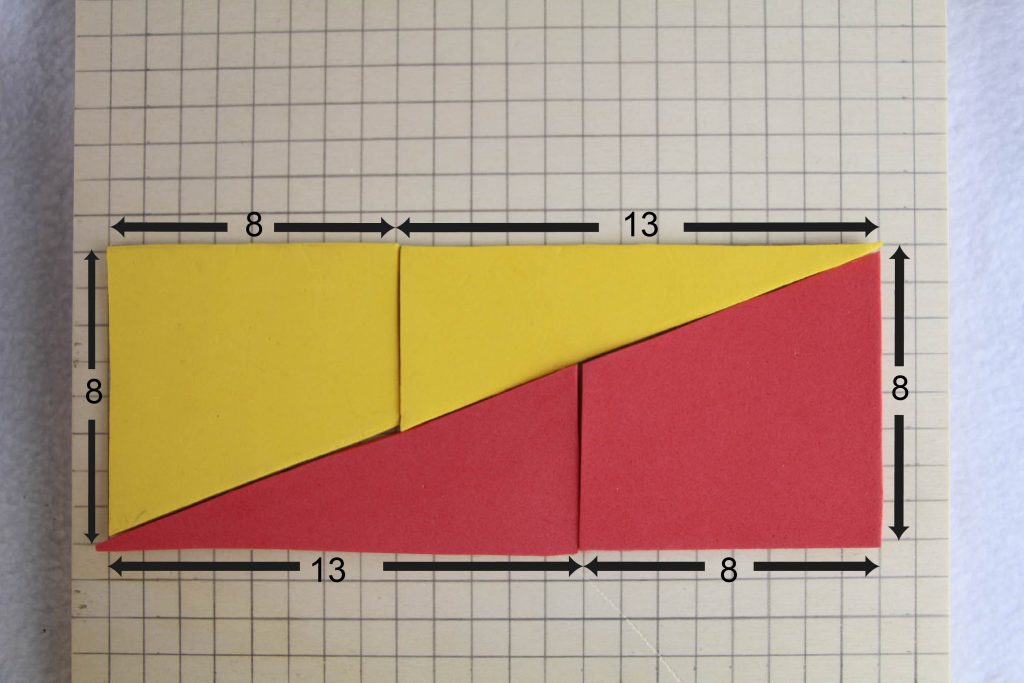
A= 8×21 = 168 
A = 13×13 = 169
Tatsächlich sind die Seitenlängen 3, 5, 8, 13 und 21 wieder Zahlen aus der Fibonacci-Folge. Zur Erklärung des ungleichen Flächeninhalts sollte man – allerdings nicht optisch – überprüfen, ob die “Diagonale” des Rechtecks tatsächlich eine gerade Strecke ist, z.B. mithilfe der Steigungen 5/13 beim Dreieck und 3/8 beim Trapez. Für diesen Trick lassen sich auch andere Fibonacci-Zahlen verwenden.
Es gibt eine Variante des uralten Nim-Spiels, bei der die Zahlen der Fibonacci-Folge eine entscheidende Rolle spielen. Deswegen kann man hier auch von Fibonacci-Nim sprechen. Es ist ein Strategiespiel für zwei Spieler, die abwechselnd Spielsteine von einem einzigen Stapel nehmen. Gewonnen hat derjenige Spieler, der den letzten Spielstein nimmt. Deswegen darf der Anfänger bei seinem ersten Nehmen nicht alle Steine wegnehmen. Anschließend gelten die Regel, jeder Spieler muss mindestens einen Stein, aber höchstens doppelt so viele wegnehmen, wie sein Gegner in der vorhergehenden Runde genommen hat. Und was haben die Fibonaccis damit zu tun? Überraschung! Ist N eine Fibonacci-Zahl gewinnt der zweite Spieler, ist sie es nicht, wird der erste Sieger.
Viel Spaß mit den Fibonaccis!