In der Mathothek hängt dieser kleine „Setzkasten“ mit verspiegelter Rückwand und einem Glastürchen, damit nicht „zufällig“ die Zahl der ca. 50 niedlichen Objekte zu- oder abnimmt, und die schönen bunten und formenreichen Würfelbeispiele doch den Besucher entzücken können. Es handelt sich dabei um einen Teil der reichen Sammlung der Mathothek von Würfeln mit verschiedensten Formen, Farben, Zwecken, Ereignismöglichkeiten, aus ganz verschiedenen Materialien, Zeiten und Kulturen.
Die anderen Würfelbeispiele befinden sich in zwei Holzbehältern. Die meisten hier in dieser flachen Holzkiste:


Jeder Besucher der Mathothek, der in der Regel nur den normalen Würfel in verschiedenen Größen, Farben, aus Holz, Glas oder Plastik kennt, ist im Anblick der Fülle von „Würfeln“ erstmal erstaunt und will natürlich wissen, was diese Objekte denn überhaupt zu Würfeln macht.
Der allseits bekannte Würfel mit den uns von klein auf bekannten Punkten für die Zahlen von eins bis sechs ist aufgrund seiner Symmetrie ein Garant dafür, dass beim ordnungsgemäßen Werfen das Ergebnis wirklich zufällig ist, d.h. dass bei längerem Würfeln jede der sechs Zahlen etwa gleich häufig fällt.
Nun ist der Kubus – der normale Würfel – einer der fünf platonischen Körper (Hexaeder). Alle platonische Körper weisen Symmetrien auf, die für die Zufälligkeit der Ergebnisse garantieren. Deswegen wundert es nicht, dass auch die vier anderen platonischen Körper (Ikosaeder, Dodekaeder, Oktaeder und Tetraeder) als Zufallsgeräte genutzt werden:

Die platonischen Körper zeigen den Weg, wie man zu weiteren Würfeln kommt. Es ist die symmetrische Struktur, die einen geometrischen Körper zum Würfel macht oder nicht. Den Antrieb dazu liefert der Wunsch noch andere Ergebnismengen als die Zahlen eins bis sechs zu erhalten, z.B. eins bis zehn.
Besonders schön ist der Würfel, der von 30 besonderen Rauten begrenzt wird. Er spielt nicht nur in der Mathematik eine große Rolle, sondern auch als Anreiz im Design. Als Würfel trägt er auch die 26 Buchstaben des Alphabets (mit vier weiteren Zeichen).

Es ist nicht schwer zu erkennen, dass dieser Würfel die faire Teilnahme für blinde und sehbehinderte Menschen ermöglicht.

Diese beiden besonders gestalteten 6er-Würfel sollen dessen Funktionen noch verstärken.

Der linke „Würfel“ ist eine andere Möglichkeit, die Zahlen von eins bis sechs zufällig zu erzeugen. Beim rechten „Würfel“ besteht die Ergebnismenge aus eins bis zehn. Hier handelt es sich um eine Verbindung von Würfel und Glücksrad. Beide Würfeltypen lassen sich symmetrisch für andere Ergebnismengen abändern.

Es gibt auch durchsichtige Würfel mit aufgemalten Augenzahlen, in deren Innerem sich ein weiterer kleinerer Würfel befindet. Als Ergebnismenge kann man die gewürfelten Zahlen beispielsweise als mehrstellige Zahlen, Summen oder Produkte verwenden.

Der linke dieser drei Würfel trägt die Zahlen 5, 10, 50, 100, 500 und 1000 in Form der entsprechenden römischen Zahlzeichen V, X, L, C, D und M. Der rechte die Zahlen von 0 bis 9 in ostarabischen Ziffern (die oben liegende Ziffer ist die Zwei. Dreht man den Würfel um etwa 90°, so erkennt man durchaus die Verwandtschaft zu unserer 2, die sich aus den westarabischen Ziffern entwickelt hat.) und der untere Kubus zeigt die üblichen Zahlen von eins bis sechs in chinesischen Zahlzeichen.

Es sind in der Würfelsammlung der Mathothek auch eine ganze Reihe Würfel, um das elementare Rechnen zu üben.

Von allen 3D-Körpern ist nun mal die Kugel derjenige mit den meisten Symmetrien. Trotzdem taugt gerade die Kugel nicht als Würfel, weil alle Punkte auf ihrer Oberfläche – überabzählbar viele – gleich wahrscheinlich sind. Diese beiden scheinbaren Kugelwürfel sind Mogelpackungen: Die beiden linken Kugeln haben im Inneren keine Hohlkugeln und der rechte „Kugelwürfel“ ist keine glatte Kugel, sondern hat kleine flache Kreise für die Zahlen von 1 bis 100.

Typisch für unsere Zeit sind diese beiden elektronischen Würfel. Sie muss man nur hart aufsetzen und darauf warten, dass nach einigem Blinken das endgültige Ergebnis leuchtet.

Nach diesen Informationen über die Welt der Würfel kann man mit frischen Augen neue Würfel entdecken und herstellen. Oft ist es hier aber nicht klar, ob alle Ergebnisse, die mit diesem Würfel möglich sind, auch dieselbe Wahrscheinlichkeit haben, bzw. wie groß die Wahrscheinlichkeiten für die jeweiligen Ergebnisse sind. Dafür lassen sich durch Experimente Näherungswerte ermitteln. Aufgrund des Gesetzes der großen Zahl, das besagt, dass sich die Werte für die relative Häufigkeit eines bestimmten Ergebnisses immer mehr der Wahrscheinlichkeit dieses Ergebnisses annähern, je mehr Zufallsversuche man macht.

Beim zufälligen Werfen einer Reißzwecke gibt es klar nur zwei Ergebnisse, nämlich Kopf oder Spitze, aber die beiden Ausfälle sind nicht gleich wahrscheinlich!
Ein solches bei vielen jungen Besucher beliebtes Würfelspiel ist das „Schweinchen-Würfeln“, bei dem vier nicht gleich wahrscheinliche Ausfälle möglich sind.

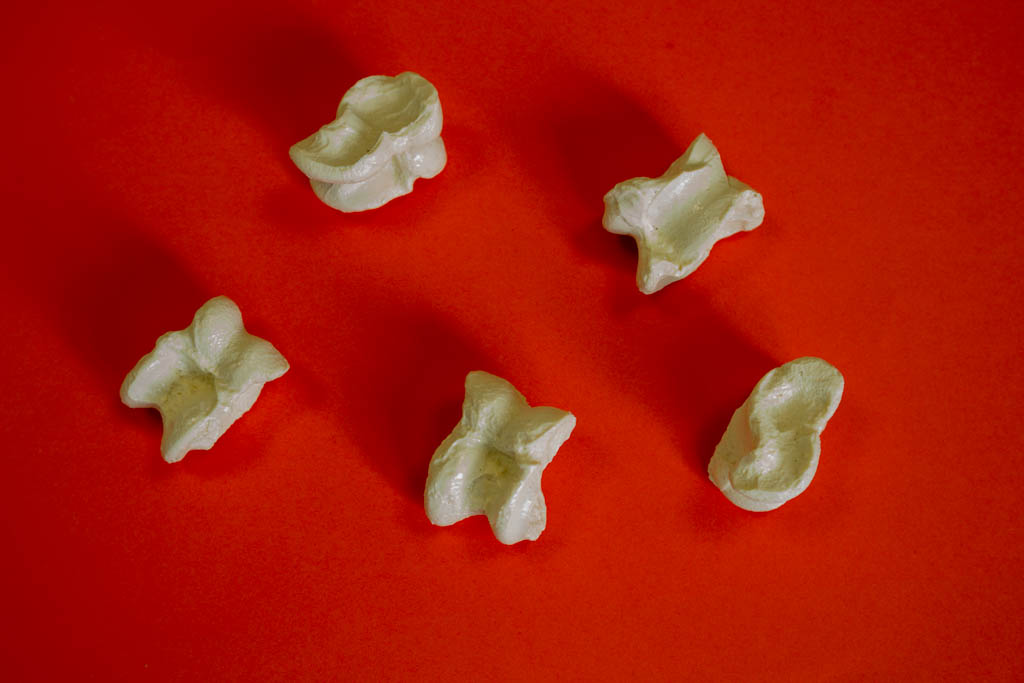
Es gibt in der Würfelsammlung der Mathothek auch fünf Astragale, das sind seit prähistorischer Zeit benutzte Würfel, die aus Sprunggelenkknochen von Paarhufern, wie Schafen, Ziegen oder Rindern gemacht wurden. Sie besitzen vier ungleiche Seiten, die man leicht unterscheiden kann und die ohne weitere Bearbeitung als Würfel verwendet werden können. Funde aus dem alten Orient zeigen, wie verbreitet diese Würfel bereits in prähistorischer Zeit waren. Noch heute wird mit Astragalen im Mittelmeerraum und in der Mongolei gespielt. Schon in Homers Ilias werden diese Würfel erwähnt. Die Regeln für solche Geschicklichkeits- und Glücksspiele sind nicht alle sicher überliefert und variierten im Laufe der Zeit und ihrer Verbreitung. Astragale wurden in Griechenland und Kleinasien auch als Orakel benutzt. Ausführlichere Hinweise zu den Astragalen findest Du in einem eigenen Artikel.
Mit den beiden nächsten Würfelspielen lassen sich Zahlen bis zu einer gewissen Größe in binärer Darstellung erwürfeln. Beispielsweise wäre das Ergebnis 11101 die Zahl 29 (rechtes Bild). Vereinbart man fünfmal zu würfeln, so lautete die größtmögliche Zahl 31. Abweichende Spielregeln können abgesprochen werden, so z.B. drei Binärwürfel zu werfen und aus den Ergebnissen die größtmögliche Zahl zu bilden.
Es gibt in der Mathothek viele Würfel-Spiele, bei denen die Ausfälle oder möglichen Ergebnisse keine Zahlen sind, sondern – mehr oder weniger ernstgemeinte – Entscheidungshilfen, z.B. über Freizeitgestaltung oder Gebete. Aber man kann auch Himmelsrichtungen oder Tierkreiszeichen erwürfeln. Natürlich können verschiedene Farben als Würfel-Ergebnisse auftreten.
Auch hier gibt es „Nicht – Würfel – Varianten“:

Wer jetzt immer noch Interesse am Würfeln hat, der kann sich mit folgendem Würfel-Spiel auseinandersetzen:

Oder er kann auch Verbindungen von Würfel und Sprache genießen:
„Alea iacta est.“ ist auch vielen Nicht-Lateinern bekannt als Redewendung „Der Würfel ist gefallen.“ oder auch im Plural „Die Würfel sind gefallen.“ Gemeint ist damit, dass eine Sache durch ein Zufallsexperiment endgültig entschieden ist. Dass die Mathothek nicht würfelt, bedeutet, dass ihr ein Plan von Kriterien zugrunde liegt, der dem Motto „Mathematik begreifbar zu machen “ gezollt ist.
Inzwischen besitzt die Mathothek, zwar keine echten antiken Astragale genannten Würfel, sondern nachgebildete Objekte. Astragale sind Sprunggelenksknochen von Schafen oder Ziegen. Sie besitzen vier ungleiche Seiten, die man leicht unterscheiden kann und die ohne weitere Bearbeitung als Würfel verwendet werden konnten. Funde aus dem alten Orient zeigen, wie verbreitet diese Würfel bereits in prähistorischer Zeit waren. Noch heute wird mit Astragalen im Mittelmeerraum und in der Mongolei gespielt. Schon in Homers Ilias werden diese Würfel erwähnt. Astragale wurden in Griechenland und Kleinasien auch als Orakel benutzt.
Spielregeln wurden uns durch die Römer überliefert. Eine beliebige Anzahl von Spielern bestimmt zunächst den Einsatz, der in die Mitte platziert wird. Reihum, im Uhrzeigersinn, würfeln die Spieler mit vier Knöchelchen. Die erreichten Punkte werden jeweils notiert. Nach 10 Runden oder einem Venuswurf ist das Spiel beendet. Gewonnen hat der Spieler mit der höchsten Punktzahl. Bei gleicher Punktzahl wird der Einsatz geteilt.
Zählweise:
- Schmalseite mit Mulde (Hund) 1 Punkt
- Breitseite ohne Mulde (Feuer) 3 Punkte
- Breitseite mit Mulde (Adler) 4 Punkte
- Schmalseite ohne Mulde (Prinz) 6 Punkte
Besondere Würfe:
- Venuswurf: Alle vier möglichen Seiten (Hund, Feuer, Adler und Prinz) auf einmal. Der Spieler gewinnt sofort das Spiel und bekommt den Einsatz.
- Nur Hunde: Geringste Punktzahl, der Spieler scheidet sofort aus.
- Viermal Feuer, Adler oder Prinz:Der Wert der Punkte wird mal vier genommen und es gibt noch 20 Extrapunkte dazu. Werden drei gleiche Seiten gewürfelt, so gibt es 10 Extrapunkte und bei zwei gleichen Seiten gibt es fünf Extrapunkte.