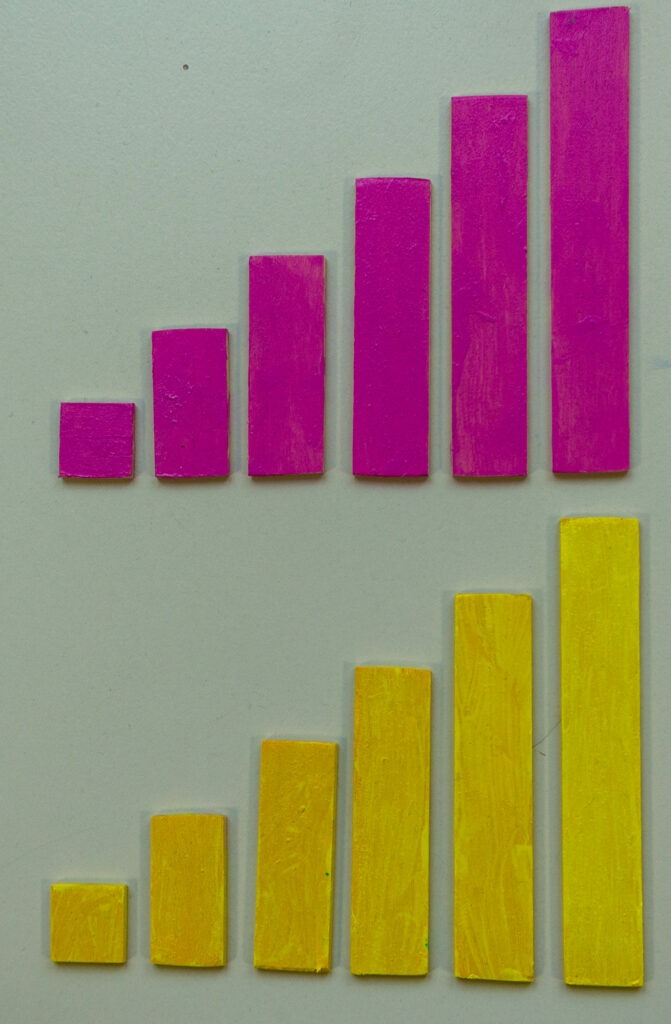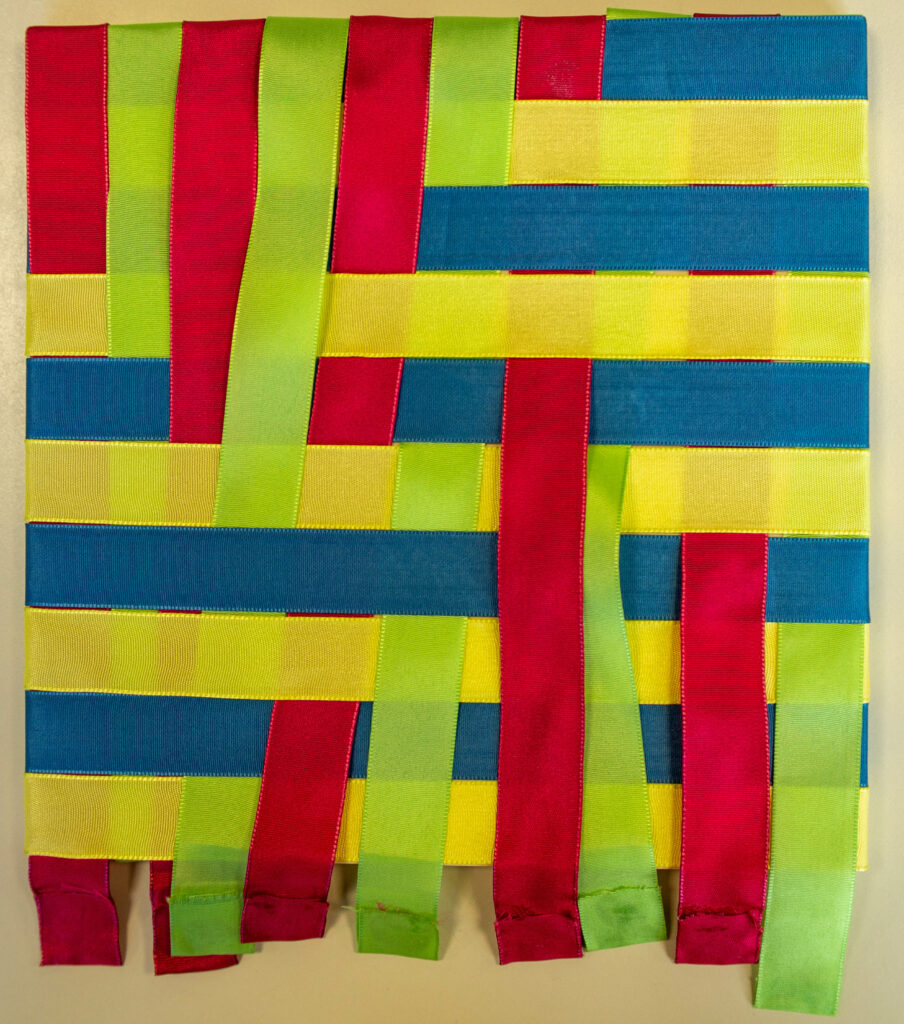Wie können wir helfen?
Es geht bei diesem Exponat um ein konstruktivistisches Gemälde von Richard Paul Lohse (1902 – 1988) mit dem Titel: Zwei und zwei gleiche Farbgruppen. 1965/69. Öl auf Leinwand. 60x60cm.
Auf dem von sinnlicher Farbkraft geprägten, mit Ölfarben auf Leinwand gemalten Bild, fallen zunächst die beiden Farbgruppen auf: die beiden Grundfarben blau und gelb einerseits und die Mischfarben rotviolett und grün andererseits. Die Farben jeder der beiden Gruppen verlaufen parallel. Je zwei Farben aus verschiedenen Gruppen sind orthogonal angeordnet. In vielen Untersuchungen ergab es sich, dass die Mehrheit der Befragten ziemlich übereinstimmend bestimmten Farben gewisse Eigenschaften und Wirkungen zugeordnet werden. so ordnet man häufig den Farben Grün und Blau eine kalten Charakter und den Farben Rot und Gelb einen warmen zu. Detailliertere Untersuchungen ergeben als die zugeordneten Eigenschaften der Farben Blau, Gelb, Grün und Rot harmonisierend, lebhaft, beruhigend und anregend als Wirkung an. In einem modernen Farbkreis, der auf dem additiven Kreis von sieben Farben Isaak Newtons basiert, sind die Farben Gelb und Blau ebenso wie Rotviolett und Grün komplementäre Farben.
Neben der Auseinandersetzung mit den Farben ist die Antwort auf die Frage nach den von ihm zu benutzenden Formen für den Maler auf dem Wege zu dem gelungenen Kunstwerk grundlegend.
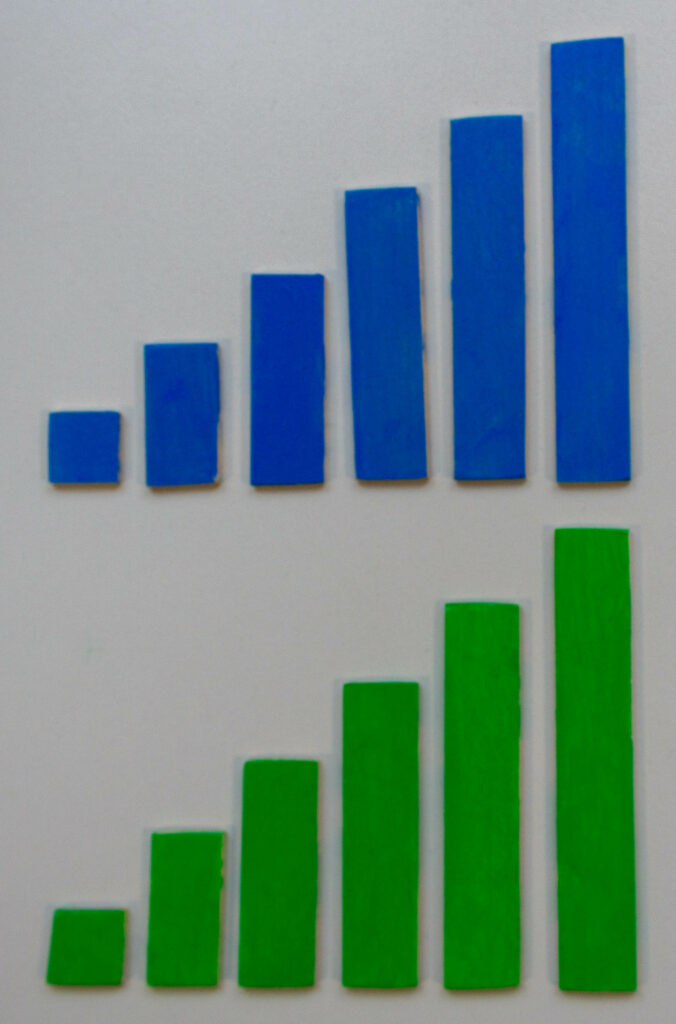
Als Formen beherrschen Rechtecke das gesamte Bild, das sie vollständig und ohne Überlappung ausfüllen. Alle Rechtecke besitzen dieselbe Breite, aber verschiedene Längen. Das kleinste Rechteck ist bei allen vier Farben ein Quadrat. Die anderen Rechtecke sind ganze Vielfache dieses Grundquadrats. In jeder Farbe gibt es acht Rechtecke. Damit besteht das gesamte Bild aus 32 Quadraten, von denen in jeder Farbe genau zwei Paare gleich groß sind. Hier liefert die Mathematik klare Möglichkeiten und Grenzen. Der Betrachter kann nun im Hinblick auf die zwei Zweierfarbgruppen immer neue mathematische Beziehungen in dem Gemälde entdecken.
Nach dem Motto: Mathematik zum Anfassen entstand ein kleines, einem “Legespiel” ähnliches, interaktives Objekt für die Mathothek. Die Rechtecke entstanden aus sehr dünnen Holzstreifen, die möglichst nahe zu den originalen Farben angemalt wurden. Zur Erleichterung der “Puzzlearbeit” gibt es einen entsprechend großen Boden mit Rahmen. Das Originalgemälde hat allerdings die Maße 60cm x 60cm. Allerdings erlaubt dieses nur 15cm lange und breite Abbild einen “konstruktiven Interpretationszugang” zu diesem Kunstwerk von Lohse, das in den 1960er-Jahren in der Hochzeit seiner konstruktivistischen Schaffensperiode entstand.
Hier sind alle 32 Rechtecke im Überblick zu sehen:
Gern kann nun jeder Besucher der Mathothek versuchen, alle diese Teile zu einem Quadrat in den gegebenen Rahmen zu legen. Oder unter zur Hilfenahme der folgenden Start-Tipps sich dem großen Vorbild zu nähern.
Hier folgen zwei Vorschläge für einen erfolgversprechenden Beginn:
Vereint man diese beiden Teillösungen, so erhält man bereits das wesentliche Gerüst für das gesamte Bild:
Man muss jetzt Symmetrie und Flechtstruktur zusammenbringen, d.h. die gelben und blauen Streifen verlaufen parallel. Ebenso tun dies die grünen und pinken:
Das kleine Abbild komplett zu machen, ist nun keine “Kunst” mehr:
Natürlich ist der einfachste Weg, nämlich das gesamte Bild einfach nachzubauen, auch eine gute Möglichkeit, die vielfältigen geometrischen Strukturen des Bildes zu entdecken und zu verstehen. In jedem Fall geht es darum, sich dem Kunstwerk konstruktiv zu nähern und mit Augen und Hand die Symmetrien, die Rolle der beiden Farbgruppen, die Flechtstruktur und vielleicht noch mehr zu entdecken.
Solange man sich an die sieben Verhaltensregeln der Mathothek hält, sind der Kreativität der Amateurkünstler keine Grenzen gesetzt. Vielleicht entstehen ja auch neue, interessante Bilder?
Ein zweites interaktives Objekt der Mathothek erlaubt eine nachvollziehende Erkenntnis der “Flechtstruktur” des Gemäldes:
Die “zwei und zwei gleiche Farbgruppen” sind hier in Form von 2x2x5=10 gleich breiten Bändern orthogonal auf einem 25cm x 25cm Sperrholzbrett befestigt. So lässt sich durch Flechten ebenfalls eine “Kopie” des Bildes herstellen:
Mithilfe von nicht mehr sichtbarem Klettband lassen sich die Bänder auch noch auf der Rückseite des Sperrholzquadrats fixieren:
Nach diesem Experiment mit dem konstruktivistischen Gemälde entdeckt man plötzlich, dass ein ästhetisches Legespiel mit ansprechend gemachten kongruenten Parallelogrammen und rechtwinkligen und gleichschenkligen Dreiecken unsere “konstruktivistische Kreativität” hinsichtlich der mehr emotionalen Herausforderung der Farben und der strengen rationalen Herausforderung der Geometrie zu einer überzeugenden Lösung zu bringen.
Eine der vielen möglichen Lösungen:
In der Mathothek hat das Angebot an Exponaten zum Thema Mathematik und Kunst einen sehr großen Stellenwert. Es gibt weitere mathematisch-künstlerische Experimentiermöglichkeiten, insbesondere zur Konkreten Kunst. So auch zwei Angebote, die durch Arbeiten der Künstlerin Ingrid Hornef angeregt wurden, z.B. zu Zufall und Ordnung:
oder die Kombinationsmöglichkeiten von gleichen Brücken:
ähnliche Angebote macht der “F-Prinzip”-Baukasten:
oder man nutzt die phantastischen Möglichkeiten von “Mathmaker”:
oder das nachgebaute Moron’sche perfekte Rechteck:
oder die perfekte Zerlegung des Quadrats in 21 verschieden große Quadrate:
Mit einem gewissen Schmunzeln erinnert dieses Objekt zu Lohses Gemälde aber auch an den Schweizer Künstler Ursus Wehrli und seine Arbeiten zum “Aufräumen von Kunst”:
Man sollte halt nie humorlos übertreiben. Auch nicht dadurch, dass man auch noch seine Merkfähigkeit mit einem Memoryspiel der Mathothek zu diesem Thema trainiert:
Die Bezeichnung konstruktivistische Kunst bezieht sich auf die Theorie, dass wir die Welt nur erkennen, wenn unser Gehirn die optischen Wahrnehmungen zu sinnvollen Deutungen verarbeitet, also mit vernünftigen Erklärungen verarbeitet. Mithilfe der zahlreichen Experimente der Mathothek zum Thema optische Täuschungen lassen sich viele grundlegende und sehr interessante Erfahrungen zur optischen Wahrnehmung unserer Welt machen. Besonders faszinierend sind hier die folgenden Objekte:
Ames’scher Raum
Scheinbare Durchdringung
Regelmäßiges Muster, oder nicht?