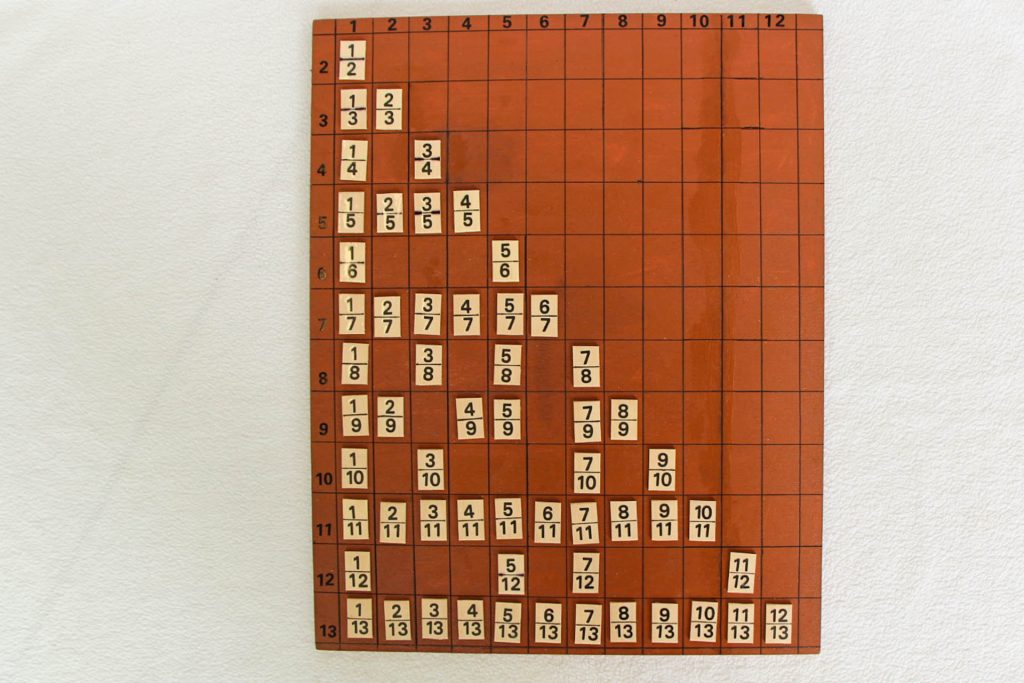Wie können wir helfen?
Der berühmte Mathematiker Leopold Kronecker (1823 – 1891) lieferte u.a. wesentliche Beiträge zur Algebra und Zahlentheorie. Er akzeptierte nur mathematische Begriffe, die durch explizite Konstruktionen definiert werden können. Er lehnte die Mengenlehre seines Schülers Georg Cantor ab und versuchte die Mathematik allein auf der Grundlage der natürlichen Zahlen aufzubauen. Berühmt geworden ist sein Ausspruch: “Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk.” Kronecker wurde durch seinen Finitismus zum Vorläufer des mathematischen Konstruktivismus.
In der Mathothek gibt es viele Exponate, die sich mit den natürlichen Zahlen beschäftigen. Besonders anschaulich und hilfreich sind die aus der eigenen Unterrichtspraxis stammenden und selbst gemachten Rechenstäbe. Das gilt insbesondere im Zusammenhang mit der Erweiterung der natürlichen durch die negativen Zahlen.
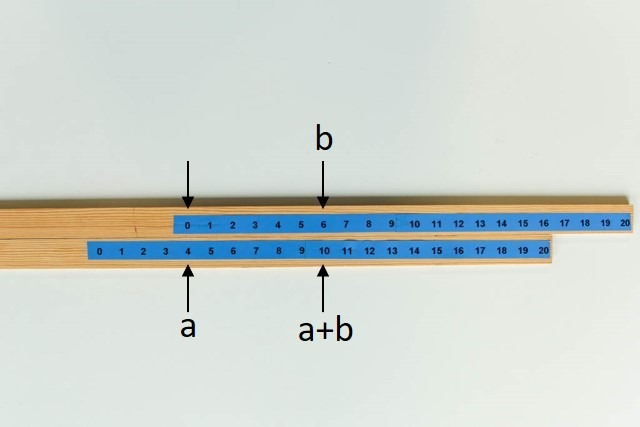
Mit den beiden Stäben, die nur natürliche Zahlen haben, kann man Regeln für die Addition und die Subtraktion herleiten:
Additionsregel:
Nehmen wir die Aufgabe 4+6. Wir stellen die 0 des oberen Zahlenstrahls über die 4 des unteren Zahlenstrahls und lesen unter der 6 das Ergebnis (4+6=)10 ab. Mit dieser Stellung der beiden Stäbe kann auch jede Summe 4+x gelöst werden, bzw. erklärt werden. Dieses Schema liefert so die Summe a+b je zweier natürlicher Zahlen a, b. Wir stellen die obere 0 über die untere Zahl a und lesen die Summe a+b unter der oberen Zahl b ab.
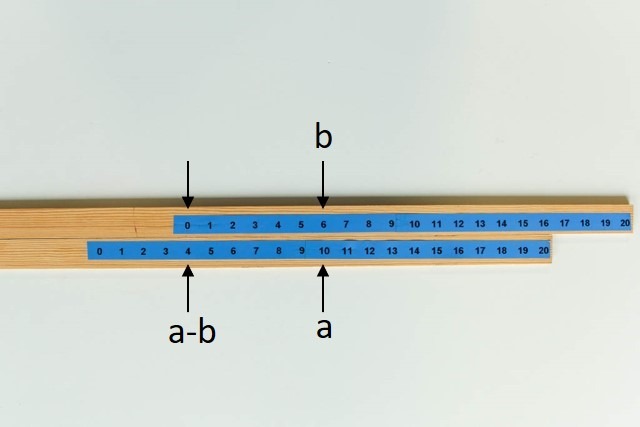
Subtraktionsregel:
Es ergibt sich daraus auch das Vorgehen bei der Subtraktion. Nehmen wir das Beispiel 10-6: Wir stellen die 10 unter die obere 6 und lesen unter der oberen 0 das Resultat (10-6=)4 ab. Um allgemein die Differenz b-a zu ermitteln, stellen wir die untere Zahl b unter die obere Zahl a und lesen unter der oberen 0 die Differenz b-a ab.
Diese beiden Regeln werden wir weiter unten auf die negativen Zahlen übertragen und damit auf den Bereich der ganzen Zahlen erweitern.
Viele Exponate in der Mathothek, die sich mit den natürlichen Zahlen beschäftigen, stehen im Zusammenhang mit der Fibonacci-Folge, die aus natürlichen Zahlen konstruiert wird. Die Folge beginnt mit 1, 1 und setzt sich dann durch Addition der beiden vorausgehenden Fibonacci-Zahlen fort: 2=1+1, 3=1+2, 5=2+3, 8=3+5 usw.
Die Zahlen der Fibonacci-Folge stehen im Zusammenhang mit dem Goldenen Schnitt und sind sowohl in der Natur wie auch in der Kunst zu finden. Die zahlreichen Exponate zu den Fibonaccizahlen in der Mathothek sind ein Bereich, in dem es viel zu entdecken und zu experimentieren gibt.
Aus einigen gegebenen Zahlen einer Folge von natürlichen Zahlen auf die Fortsetzung und das Baugesetz einer Folge zu schließen, ist regelmäßig Teil von Intelligenztests. In der Mathothek gibt es auch hierzu ein interaktives Objekt:
Viele Informationen über die Eigenschaften der natürlichen Zahlen liefert uns auch das so einfach aufgebaute Schema des Pascal’schen Dreiecks.
Außer den Einsen am Rande des Dreiecks ist jede Zahl immer die Summe der beiden Zahlen, die über ihr stehen. Auf dem unteren Bild sieht man eine fraktale Struktur, die entsteht, wenn man im Pascal’schen Dreieck gerade und ungerade natürliche Zahlen verschieden färbt.
Neben der Tatsache, dass das Pascal’sche Dreieck der Reihe nach die Binomialkoeffizienten liefert, lassen sich eine Fülle weiterer Entdeckungen über die Eigenschaften der natürlichen Zahlen machen. Zu diesem, wie zu allen anderen hier genannten Exponaten, gibt es im Katalog noch mehr Hinweise und Bilder.
Jede natürliche Zahl, die nur durch 1 und sich selbst teilbar ist, nennt man Primzahl. Allerdings zählt die 1 nicht zu ihnen. Deshalb gilt, dass genau die natürlichen Zahlen prim sind, die genau zwei Teiler haben. Der unten gezeigte Zahlenstrahl gehört zu einem interessanten Exponat der Mathothek: zur Goldbach’schen Vermutung. Dabei handelt es sich um die Behauptung, dass jede gerade Zahl, die größer als 2 ist, als Summe von zwei Primzahlen dargestellt werden kann. Obwohl diese Aussage so einfach und verständlich formuliert werden kann, hat aber bis heute noch keiner einen Beweis oder eine Widerlegung gefunden.
Bei dem nächsten Experiment, das nach dem antiken Mathematiker Eratosthenes “Sieb des Eratosthenes” genannt wird, lassen sich aus einem endlichen Abschnitt des Zahlenstrahls die Primzahlen systematisch “heraus sieben”, indem man die echten Vielfachen der Zahlen schrittweise streicht. In diesem Experiment der Mathothek werden nach und nach die 1 und dann alle echten Vielfachen von 2, 3 usw. bedeckt. Die am Schluss übriggebliebenen Zahlen sind genau die Primzahlen zwischen 1 und 100.
Das Unbefriedigende an der Menge der natürlichen Zahlen (einschließlich der Null) ist, dass sich zwar alle Additions- und Multiplikationsaufgaben immer lösen lassen, nicht aber jede Subtraktions- und jede Divisionsaufgabe. Deswegen lernen die Schüler neue Zahlen kennen, nämlich die Bruchzahlen. Man könnte auch zunächst die natürlichen Zahlen durch die negativen Zahlen erweitern und damit zu den ganzen Zahlen kommen. Aber aus didaktisch-pädagogischen Gründen zieht man die Brüche vor. Ein Drittel einer Pizza ist der Erfahrung eines Kindes vielleicht näher als minus 20 Euro.
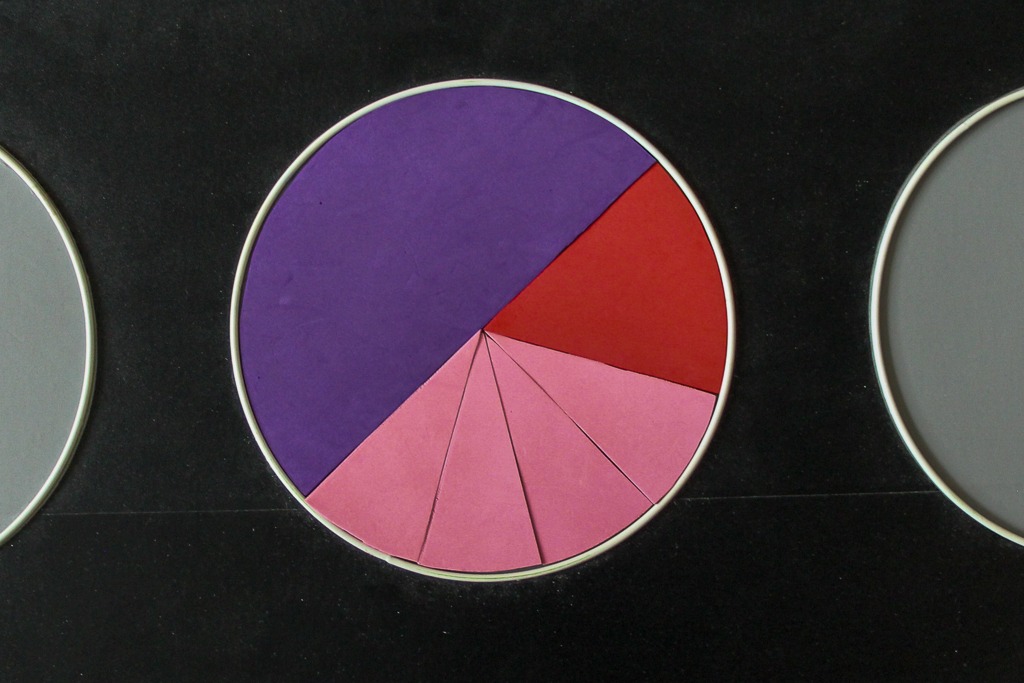
Zur anschaulichen Einführung der Brüche und der Bruchzahlen dient das “Pizza-Exponat” der Mathothek. Auf einer schwarzen Platte sind acht weiße Kreisringe angebracht. Dazu gibt es acht verschieden farbige und in “Tortenstücke” geschnittene Kreise aus Moosgummi, die in 2, 3, 4, 5, 6, 8, 10 und 12 gleich große Sektoren geschnitten wurden. Mit ihnen lassen sich die entsprechenden Brüche 1/2, 1/3, 2/3, 1/4, 2/4, 3/4 usw. darstellen.
Aus diesem Umgang mit den Brüchen gelingt dann auch der Übergang zu den abstrakten Bruchzahlen, wenn man erkannt hat, dass verschiedene Brüche gleich große Teile des Kreises bedecken können, z.B. 1/4 und 2/8, 2/5 und 4/10 oder auch 1/2, 2/4, 4/8, 3/6, 6/12 und 5/10. Auf dem Foto sieht man, dass 1/3, 2/6, und 4/12 die gleiche Fläche des Kreises bedecken, d.h. 1/3, 2/6 und 4/12 sind drei verschiedene Namen für ein und dieselbe Bruchzahl. Es gilt somit 1/3=2/6=4/12= …
Auf diesem Foto ist anschaulich dargestellt, dass 1/2=2/4=4/8=5/10=3/6=6/12 gilt.
Alle Brüche, die denselben Kreissektor belegen, sind nur verschiedene Namen für dieselbe Bruchzahl. Man erkennt die Möglichkeit, Brüche zu erweitern und zu kürzen. Erweitert wird ein Bruch, indem man Zähler und Nenner eines Bruchs mit derselben natürlichen Zahl multipliziert. Einen Bruch zu kürzen bedeutet, dass man seinen Zähler und seinen Nenner mit derselben Zahl dividiert. Dabei muss diese natürliche Zahl jedoch ein gemeinsamer Teiler von Zähler und Nenner dieses Bruches sein. Alle Brüche, die durch Kürzen und Erweitern ineinander überführt werden können, sind somit nur verschiedene Namen für dieselbe Bruchzahl.
Um zwei Bruchzahlen zu addieren oder zu subtrahieren, müssen ihre beiden Brüche gleichnamig gemacht werden, d.h. durch Erweitern oder Kürzen müssen sie “auf denselben Nenner gebracht” werden. Auf den folgenden Fotos sind die beiden Aufgaben 1/3+1/4 und 1/3-1/4 gelöst worden. Im ersten Schritt werden die beiden Brüche gleichnamig gemacht, d.h. 1/3=4/12 und 1/4=3/12. Anschließend erhalten wir im Beispiel durch Addition der Zähler die Summe 1/3+1/4=4/12+3/12=7/12:
Für die Differenz 1/3-1/4 werden dann ihre Zähler subtrahiert. Das Ergebnis lautet dann 1/12:
Eine gute spielerische Übung für jüngere Schüler besteht darin, die acht “Pizza-Teller” möglichst bunt, aber korrekt zu belegen:
Für jede Bruchzahl gibt es nur eine eindeutige Grunddarstellung. Bei der Grunddarstellung kann man nicht mehr kürzen, d.h. dass Zähler und Nenner dieses Bruchs nur 1 als größten gemeinsamen Teiler haben.
Jede Bruchzahl lässt sich auch in Dezimalschreibweise darstellen, indem man einen Bruch dieser Bruchzahl nimmt und dann den Zähler durch den Nenner dividiert: 5/10=0,2, weil 5:10= 0,2 ergibt. 5/3=1,66666…, weil 5:3=1,66666… ist.
Schreibt man eine Bruchzahl im Zehnersystem , so gibt es – im Gegensatz zur Bruchschreibweise – nur eine Darstellung: 1/4=2/8=36/144=…=0,25, 6/18=1/3=15/45=…=0,33333… , 10/7=1,42857142857… oder 1/12=0,083333… Jede Bruchzahl lässt sich im Zehnersystem – aber auch im Binärsystem und in jedem anderen Stellenwertsystem – als Kommazahl schreiben. Dabei gibt es entweder nur endlich viele Nachkommastellen oder eine Periode, d.h. ab einer bestimmten Stelle wiederholt sich ein bestimmter Ziffernblock unendlich oft.
Wesentlich tiefer in die Welt der Bruchzahlen führt die Frage: “Wie viele Bruchzahlen gibt es überhaupt?” Gibt es “mehr” Bruchzahlen als natürliche Zahlen? Dazu gibt es ein interaktives Exponat der Mathothek, mit dem man erfahren kann, dass es zwar unendlich viele Bruchzahlen gibt, aber dass sie sich “nummerieren” lassen, d.h. dass sie umkehrbar eindeutig den natürlichen Zahlen zugeordnet werden können, dass sie also abzählbar unendlich sind.
In dem Bereich der Bruchzahlen sind nun alle Additions-, Multiplikations- und Divisionsaufgaben lösbar. Wesentlich bei dieser ersten Erweiterung des Zahlbereichs der natürlichen Zahlen ist, dass die alten “vom lieben Gott gemachten natürlichen Zahlen” in ihr enthalten sind: Den natürlichen Zahlen entsprechen die Bruchzahlen, bei denen die Zähler natürliche Vielfache des Nenners sind. Beispielsweise sind die Bruchzahlen 9/3, 72/24, 3/1 usw. Bruchdarstellungen der natürlichen Zahl 3, 25/5, 30/6, 1000/200, 5/1 usw. andere Namen für die natürliche Zahl 5.
Leider lassen sich auch nach dieser Zahlbereichserweiterung mit den Bruchzahlen noch immer nicht alle Aufgaben der vier Grundrechnungsarten lösen. So besitzen nicht alle Subtraktionsaufgaben immer eine Lösung, beispielsweise die Gleichung 3/10-1/2=x (⇔ x+1/2=3/10) oder 7-12=x (⇔ x+12=7).
Auch die Gleichung 5/2:0=x hat keine Lösung. Jede Division durch null ist verboten und muss es auch bleiben, weil sonst die Mathematik zusammenbrechen würde. Nehmen wir einmal an, 7:0 wäre gleich der Zahl z, dann würde die Probe 7=z⋅0 ergeben. Das ist aber völlig unmöglich, denn jede Zahl z ergibt multipliziert mit 0 wieder 0.
Dagegen ist das andere Problem durch eine weitere Zahlbereichserweiterung lösbar. Durch die Erweiterung der Bruchzahlen mit den negativen Bruchzahlen sind nämlich dann auch alle Subtraktionsaufgaben in der neuen Zahlenmenge lösbar. Die Elemente dieses neuen Zahlbereichs nennt man rationale Zahlen.
In der Schule werden, nachdem man die natürlichen Zahlen zuerst zu den Bruchzahlen erweitert hat, im nächsten Schritt zunächst – wieder aus didaktischen Überlegungen – um die negativen ganzen Zahlen bereichert. Dabei geht man zunächst wieder von “Gottes natürlichen Zahlen” aus, um dann durch Übertragung zu den negativen Brüchen und somit zu den rationalen Zahlen zu gelangen. Mithilfe unserer Rechenstäbe lassen sich die negativen ganzen Zahlen sehr gut begreifbar einführen. Mit zwei Stäben, die nur die natürlichen Zahlen besitzen, sehen wir die Unlösbarkeit der Aufgabe 5-8. Wir stellen unter die obere 8 die untere 5 und lesen das Ergebnis unter der oberen 0 ab (Subtraktionsregel). Aber da steht nichts.
Der Rechenstab mit dem Zahlenstrahl der natürlichen Zahlen wird jetzt zur Zahlengeraden mit den negativen ganzen Zahlen erweitert:
Der obere Rechenstab enthält nur die natürlichen Zahlen. Der zweite Stab enthält spiegelbildlich die negativen ganzen Zahlen (rot), die positiven ganzen Zahlen (blau) entsprechen den natürlichen Zahlen, sie sind also in der Erweiterung zu identifizieren.
Betrachten wir nun die Aufgabe von vorhin 5-8=(+5)-(+8). Zunächst stellen wir die obere +8 über die untere +5 und lesen dann unter der oberen 0 das Ergebnis [(+5)-(+8)=]-3 ab. In dem erweiterten Zahlenbereich der ganzen Zahlen besitzt jetzt die oben in der Menge der natürlichen Zahlen nicht lösbare Subtraktionsaufgabe jetzt eine Lösung.
Hier ein Beispiel für die Addition einer negativen und einer positiven Zahl, die Aufgabe (-4)+(+9):
Wir stellen die obere 0 über die untere -4 und lesen unter der oberen +9 das Ergebnis +5[=(-4)+(+9)]ab. Auch hier können wir die Probe mit der Subtraktionsregel machen: +5-(+9)=-4.
Als nächstes Beispiel folgt eine Subtraktionsaufgabe: (-3)-(+2):
Wir stellen über die untere -3 die obere +2 und lesen (Subtraktionsregel) unter der oberen 0 das Ergebnis -5 ab. Die Probe erfolgt dann mithilfe der Additionsregel: (-5)+(+2)=-3.
Betrachten wir die Aufgabe (-8)+(+5): Wir stellen die obere 0 über die untere -8 und lesen unter der +5 das Ergebnis -3 ab. Die Probe können wir wieder mit der Subtraktionsregel machen: (-3)-(+5)=-8.
Als nächstes Beispiel ermitteln wir (-7)+(-5):
Wir schieben die obere 0 über den ersten Summanden -7 und lesen unter der oberen -5 das Ergebnis -12 ab. Auch hier machen wir mit der Subtraktionsregel die Probe: (-12)-(-5)=-7.
Jetzt lösen wir die Aufgabe (-5)-(-8)=+3:
Wir schieben über die untere -5 die obere -8 und finden das Ergebnis unter der oberen 0, nämlich +3 (Subtraktionsregel). Hier benutzen wir für die Probe natürlich die Additionsregel: (+3)+(-8)=-5.
Noch ein Beispiel soll zeigen, wie man durch den experimentierenden Umgang mit den Rechenstäben zu weiteren Regeln zum Rechnen mit den ganzen Zahlen gelangen kann: Die Aufgabe lautet 0-(-5):
Wir stellen die untere 0 unter die obere -5 und lesen unter der oberen 0 das Ergebnis +5 ab. Also ist 0-(-5)=+5 richtig. Ebenso lassen sich die Gleichungen 0-(+5)=-5, 0+(-5)=-5 und 0+(+5)=+5 zeigen.
Vielleicht fällt Dir auf, dass bei jeder Verschiebung der beiden Rechenstäbe die beiden untereinander stehenden Zahlen jeweils dieselbe Differenz darstellen. Ähnlich wie bei den Brüchen und den Bruchzahlen sind alle Zahlenpaare, die dieselbe Differenz aufweisen, verschiedene Namen für dieselbe ganze Zahl, z.B. stellen 10-3, 12-5, 2-(-5), 3-(-4), (-5)-2, 7-0 … alle dieselbe Differenz dar und somit dieselbe ganze Zahl, ebenso tun dies die Differenzen 2-11, 5-14, (-3)-6, 0-9, …
Bei dieser Erweiterung von den natürlichen zu den ganzen Zahlen lässt sich im Hinblick auf die Anordnung der Zahlen das wichtige Prinzip der Kontinuität demonstrieren: Betrachten wir die natürlichen Zahlen, so sehen wir, dass sich der Größe nach anordnen lassen, anschaulich am Zahlenstrahl zu sehen:
Für die positiven ganzen Zahlen, die ja mit den natürlichen identisch sind, bleibt die Anordnung erhalten. Auf die “symmetrischen” negativen Zahlen wird die Anordnung aber nicht spiegelbildlich übertragen, sondern so, dass auf der Zahlengeraden die Anordnung “durchgängig” ist. Zwar gilt 15 ist größer als 7, aber -7 ist größer als -15. Um diese etwas fremd anmutende Konsequenz ein wenig abzufangen, wird der Betrag einer Zahl eingeführt: Betrag von (+7)=Betrag von (-7)= 7 und Betrag von (-15)=Betrag von (+15)=15. Der Betrag von 0=0. Beim Betrag einer ganzen Zahl handelt es sich also um den Abstand dieser Zahl vom Nullpunkt.
Durch die einfache Ausdehnung der (Vorzeichen-)Regeln auf die Bruchzahlen ist der Zahlbereich der rationalen Zahlen vollständig und erlaubt es, die Grundrechenarten Addition und Multiplikation, aber auch deren Umkehrungen, nämlich Subtraktion und Division uneingeschränkt auszuführen. Diese Stufe der schrittweisen Erweiterung der Zahlbereiche von den natürlichen Zahlen zu den rationalen Zahlen ist damit ein in vielfacher Hinsicht – mit Ausnahme der Division durch null – eine sehr befriedigende Lösung.
Aber die Mathematiker waren damit noch nicht zufrieden. Da gibt es ja auch noch die wichtigen Gleichungen mit Potenzen von x, wie beispielsweise die oben beschriebene Gleichung x2=2. So stießen schon Pythagoras und seine Jünger bei der Untersuchung ihres heiligen Zeichens – dem Pentagramm – auf seltsame Schwierigkeiten, die für sie so besonders problematisch waren, weil die Pythagoreer die feste Überzeugung vertraten, “dass alles Zahl sei” und meinten damit, dass alles durch Verhältnisse zwischen natürlichen Zahlen bestimmt sei. Dieses Prinzip sahen sie besonders überzeugend in ihrer Musiklehre verwirklicht.
Was ist mit der Länge der Diagonalen in einem Quadrat mit der Seitenlänge eins?
Mit dem folgenden Objekt in der Mathothek – einem bunten Legespiel für Kinder – lässt sich das “Problem” anscheinend leicht lösen.
Dazu nehmen wir an, dass die beiden kleinen Quadrate die Seitenlänge 1 besitzen. Aus den vier Dreiecken lässt sich dann ein Quadrat zusammensetzen, dessen Fläche so groß ist wie die der beiden kleinen Quadrate zusammen, also 2. Damit gilt für seine Diagonale d die Gleichung d2=2. Aber was bedeutet dann √2?
Unser Taschenrechner ist hier auch keine wirkliche Hilfe und nur in der Lage, Näherungen für unsere gesuchte Aufgabe zu liefern. Dass das so ist, lässt sich leicht zeigen, indem man seinen angegebenen, aber ungerundeten Wert quadriert, z.B. d=”√2″=1,41421356 → d2=1,999999993.
Will man, dass die Gleichung d2=2 eine Lösung besitzt, wofür ja sehr stark die geometrische Anschauung der Existenz der Diagonalen spricht, so wird eine weitere Zahlbereichserweiterung notwendig. Dieser Schritt zu einer nächsten Zahlbereichserweiterung führt zu den irrationalen und damit zu den reellen Zahlen. Danach kommt – schulisch gesehen – die Endhaltestelle: der Zahlenbereich mit den imaginären und somit den komplexen Zahlen.