Wie können wir helfen?
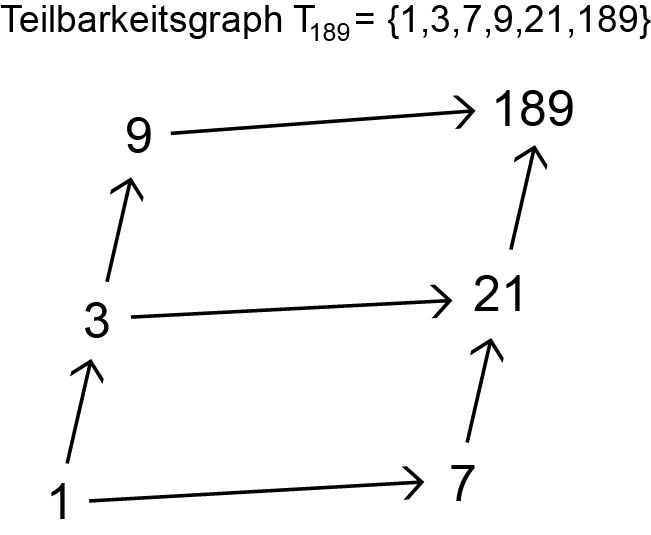
Jeder ungerichtete Graph wird zum knoten-gefärbten bzw. zum kanten-gefärbten Graphen, indem man jedem Knoten bzw. jeder Kante eine Farbe zuordnet. Ungerichtet heißt ein Graph dann, wenn die Kanten “keine Pfeile”, sondern einfache Linien sind. Zum besseren Verständnis ein Beispiel für einen gerichteten Graphen: Es handelt sich um einen Teilbarkeitsgraphen. Knoten sind die Teiler der Zahl 189, d.h. T189={1, 3, 7, 21, 9, 189}. Eine gerichtete Kante verbindet Teiler mit Vielfachem. Dabei bleiben alle Pfeile weg, die durch einen Pfad aus mehreren Pfeilen ersetzt werden können. So beispielsweise fehlt hier der Pfeil von 1 zu 21 (1→7→21).
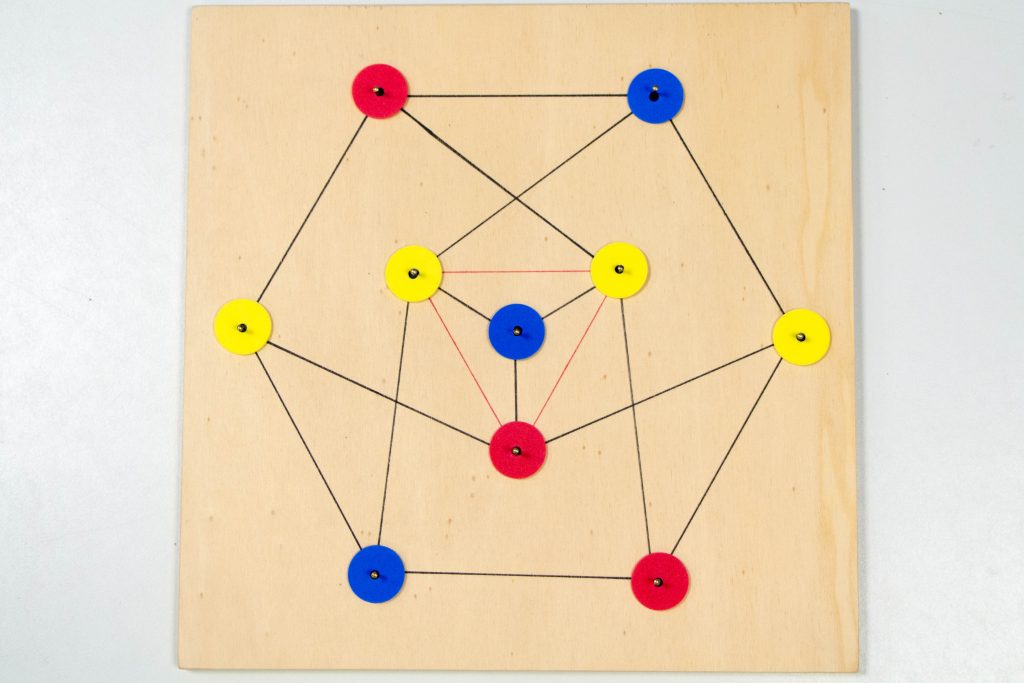
Ein ungerichteter Graph wird in diesen beiden Beispielen erst zum knoten-gefärbten und dann zum kanten-gefärbten Graphen:
Bei diesem knotengefärbten Graphen reichen – wie das Bild zeigt – drei Farben aus, um alle Knoten so zu färben, dass keine zwei durch eine Kante verbundenen Knoten dieselbe Farbe bekommen. Dies gilt allerdings nur für den schwarzen Graphen (ohne die drei roten Kanten). Eine solche Knotenfärbung, bei der keine benachbarten Knoten dieselbe Farbe haben, heißt in der Graphentheorie eine zulässige Färbung.
Die Färbung der Kanten des schwarzen Graphen gelingt nicht mit nur drei Farben. Für die letzten zwei Kanten brauchen wie eine vierte Farbe. Die Farbe Grün ist im Exponat der Mathothek als vierte Farbe vorhanden.
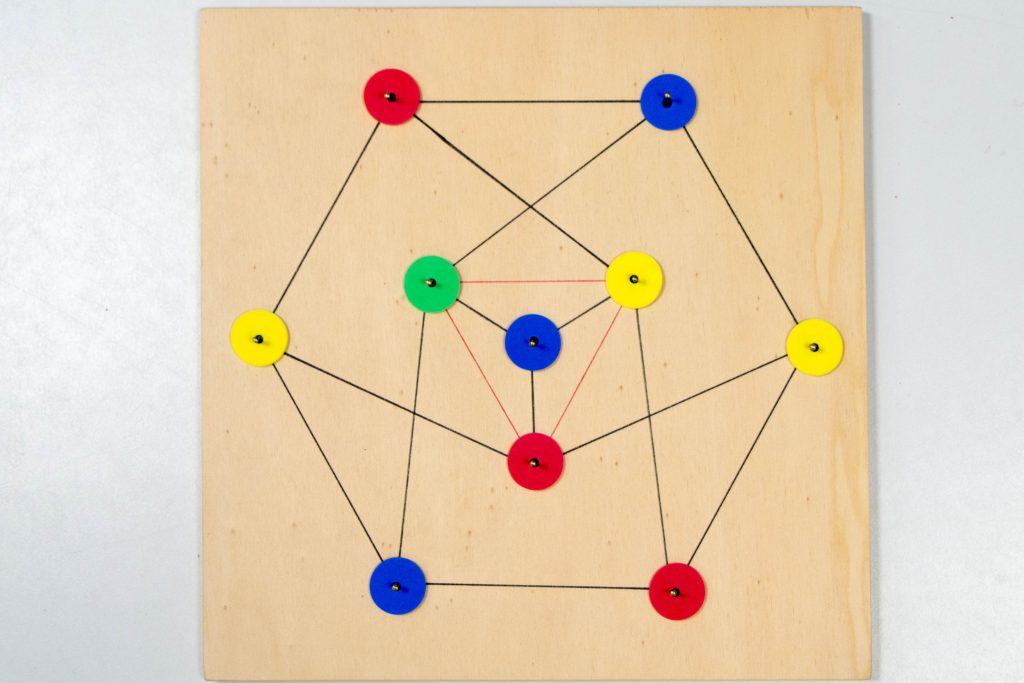
Was passiert, wenn wir jetzt die roten Kanten mit zu unserem Graphen rechnen? Das Färbungsproblem ist dann nur mit einer weiteren Farbe zu machen:
Schuld daran ist das Dreieck in der Mitte. Wenn man nur drei Farben zur Verfügung hat, lassen seine vier Knoten und sechs Kanten keinen Ausweg übrig, als zwei durch eine Kante verbundene Knoten dieselbe Farbe zuzuordnen.
Viele Fragen und Probleme – nicht nur innermathematische – lassen sich mithilfe geeigneter gefärbter Graphen bearbeiten und für sie Lösungen oder Algorithmen finden.
Ein klassisches Problem ist die Frage, ob sich jede Landkarte mit vier verschiedenen Farben so einfärben lässt, dass keine zwei Länder mit einem Stück gemeinsamer Grenze dieselbe Farbe bekommen müssen. Dass es mit fünf Farben möglich ist, wurde bereits 1891 von Julius Petersen bewiesen. Manchmal ging es auch mit nur drei Farben. Lange Zeit blieb es aber nur bei der Vermutung, dass bereits vier Farben ausreichen müssten.
Dieses so genannte Vier-Farben-Problem wurde graphentheoretisch übersetzt in die Frage, ob ein planarer Graph mit höchstens vier Farben zulässig knoten-gefärbt werden kann.
Inzwischen ist diese Vier-Farben-Satz-Frage mithilfe intensiven Einsatzes von Computerarbeit positiv beantwortet. Jedoch gibt es von vielen Mathematikern noch immer Kritik und Widerstände gegen diesen “Computerbeweis”, und das Problem des Computerbeweises ist ein ganz wichtiges und das Selbstverständnis der Mathematiker betreffendes.
Ganz ohne Computer, aber mit ordentlicher Denkarbeit ist das folgende in der Mathothek vorhandene Spiel, das an das Vier-Farben-Problem erinnert, zu machen:
Die Herausforderung ist hier, auf der quadratischen Fläche entsprechend dem aufgezeichneten Grundriss-Muster die verschiedenen roten, gelben, blauen und grünen Quadrate so anzuordnen, dass nie zwei Quadrate mit derselben Farbe, auch mit einem Teil ihrer Kanten aneinander zu liegen kommen.
Erster Versuch mit Fehler:
Hier eine Lösung, aber gleichfarbige Ecken stoßen mehrfach aneinander:
Eine noch größere Herausforderung ist es, bei der Belegung auch noch zu vermeiden, dass Quadrate mit derselben Farbe sich mit einer Ecke berühren, d.h. auch in der Diagonalen sollen sich keine zwei Quadrate mit derselben Farbe berühren. Wer schafft es? Oder wer zeigt, dass es unmöglich ist? (Lösung befindet sich ganz am Ende dieses Artikels.)
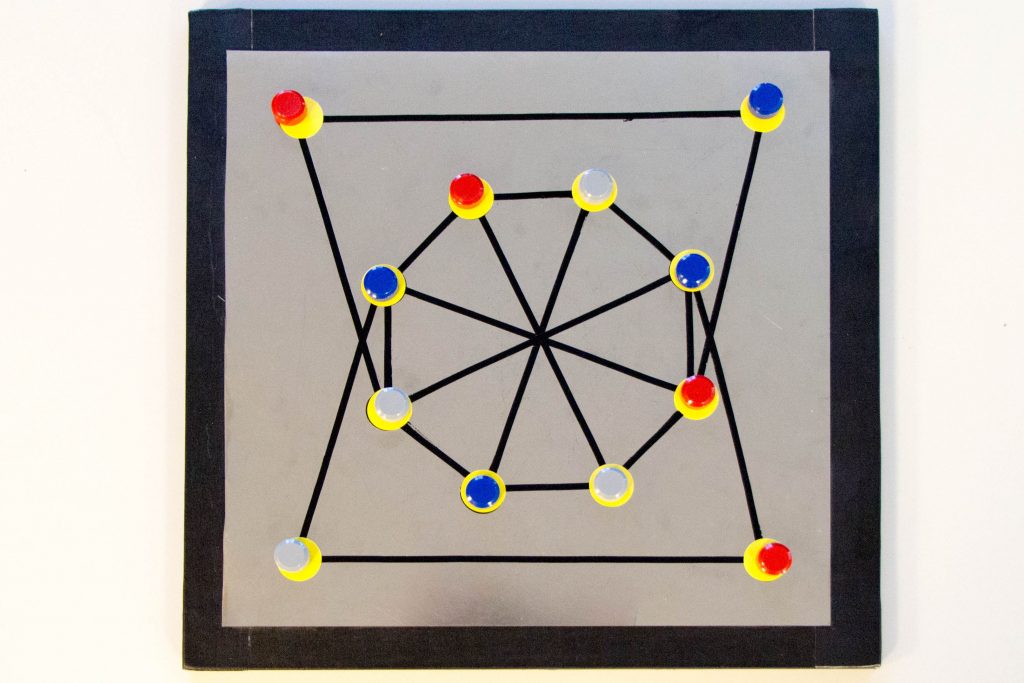
Zu dem folgenden Exponat der Mathothek gehört eine Metallplatte mit einem Graphen aus schwarzen Kanten und gelben Knoten. Außerdem braucht man die roten. gelben und grauen Magnete.
Bei dieser Aufgabe geht es darum, den gegebenen Graphen zulässig zu färben, d.h. die roten, blauen und grauen Magnete so auf die gelben Punkte zu verteilen, dass keine durch eine schwarze Linie verbundenen zwei Punkte dieselbe Farbe besitzen.
Hier ist eine Lösung.
In der Mathothek gibt es noch einen interessanten Graphen: Er wird Petersen-Graph genannt und ist u.a. sehr symmetrisch.
Versucht man diesem Petersengraphen die Kanten zu färben, gelingt dieses nicht mit nur drei Farben. Dabei erkennt man schnell, dass es nicht an der eigenen Unzulänglichkeit. Beginne entweder mit dem äußeren Pentagon oder dem inneren Pentagon, so erkennst Du die Notwendigkeit, eine vierte Farbe zu benutzen.
Eine Lösung der “Superaufgabe”:
Kein Paar farbgleicher Quadrate stößt mit zwei seiner Kanten, aber auch nicht mit zwei seiner Ecken zusammen.